Sierpinski triangle

The Sierpiński triangle is a fractal that can be constructed from any triangle.

Sierpinski Triangle

Pavement of the Basilica of Saint Mary in Cosmedin in Rome; with a geometric pattern that recalls the triangle of Sierpinski (centuryVIII)

Construction

By dilations

As in most fractals, there are several ways to obtain the same figure (triangles). In this case, all the processes imply the three dilations centered on the vertices of the triangle, with a ratio of 1/2. Let's note them h_a, h_b, and h_c.
It is easy to see that this figure contains three reductions of itself: Triangle ADE with all its contents is an exact reduction of triangle ABC, and the same can be said of CDF and BEF. These three clones are just the ABC images for h_a, h_b and h_c. And since there are no points of the fractal outside these three reductions, it can be written (T designates the Sierpiński triangle):

In other words, T is invariant by the map of the plane defined as follows: f(M) = {h_a(M), h_b(M), h_c(M)}, where M is any point in the plane. This application is more abstract than it seems because its arrival set (codomain) is not the plane itself but the parts of it, that is, the set of all possible figures of the plane. The domain of f can be extended to the parts of the plane as follows: f(F) = h_a(F) ∪ h_b(F) ∪ h_c(F) where F is any figure in the plane.
Seen this way, T is a fixed point of f. The only one, apart from the empty set, of little geometric interest.
T is also an attractor of the map f: if a (preferably simple) figure T₀ is considered, and its successive images T₁ = f(T₀), T₂ = f(T₁) = f ²(T ₀)... T_n = f ⁿ(T₀)... then the sequence T_n approximates the Sierpiński triangle.

In the following figure, the triangle ABC has been taken as the initial figure:

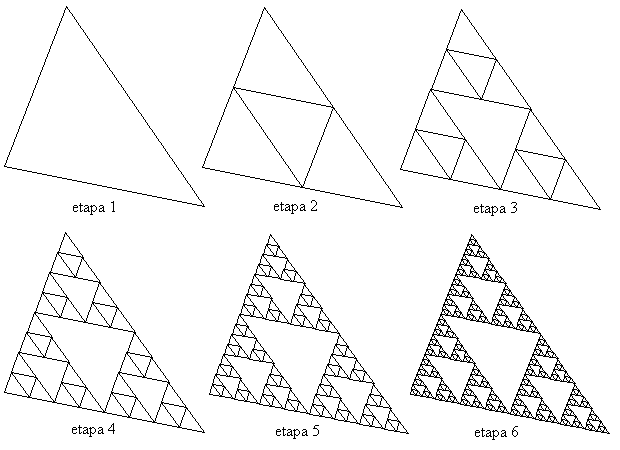
Iterating from a point

You can also build T from any random point M and, to simplify programming, randomly choose an image between h_a(M), h_b(M) and h_c(M) (in each step) instead of always taking all three. This allows to make a program without recursion, but of course, it brings a disadvantage: the number of steps to obtain a satisfactory figure will be much longer (in each step only one point is drawn):

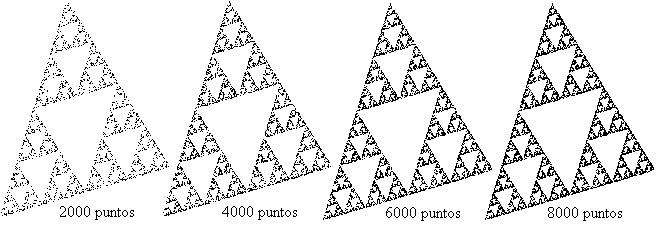
Relation to the Cantor set

If the Sierpiński triangle is intersected by a straight line parallel to one of its sides, we obtain a figure that is highly related (and similar) to the Cantor set.

Fractal dimension

The Sierpinski triangle has a Hausdorff-Besicovitch fractal dimension coincident with its homothety fractal dimension equal to:

DHB=ln 3ln 2≈ ≈ 1,584962501{displaystyle D_{HB}={frac {ln 3}{ln 2}approx 1,584962501}

Equally easy is to find the fractal dimension using an iterative system of functions, formed by three contractive functions with Lipschitz constant 1/2 from where it follows that the Hausdorff-Besicovitch fractal dimension satisfies:

3(12)DHB=1Δ Δ DHB=ln 3ln 2{displaystyle 3left({frac {1}{2}}}{D_{HB}}}}=1quad Leftrightarrow quad D_{HB}={frac {ln 3}{ln 2}}}}}}