Set

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

The various polygons in the image constitute a set. Some of the elements of the set, besides being polygons are regular. The collection of the latter—the regular polygons in the image—is another set, in particular a subset of the first.

In mathematics, a set is a collection of elements considered itself as an object. The elements of a set can be the following: people, numbers, colors, letters, figures, etc. An element (or member) is said to belong to the set if it is defined as somehow included within it.

Example: the set of colors of the rainbow is:

AI = {red, orange, yellow, green, blue, dye, violet}

A set is usually defined by a property that all its elements possess. For example, for natural numbers, if the property of being a prime number is considered, the set of prime numbers is:

P = {2, 3, 5, 7, 11, 13,...}

A set is defined only by its members and nothing else. In particular, a set can be written as a list of elements, but changing the order of that list or adding repeating elements does not define a new set. For example:

S = {lights, Tuesday, Wednesday, Thursday, Friday} = {martes, Friday, Thursday, Monday, Wednesday}

AI = {red, orange, yellow, green, blue, dye, violet} = {yellow, orange, red, green, violet, dye, blue}

Sets can be finite or infinite. The set of natural numbers is infinite, but the set of planets in the solar system is finite (it has eight elements). Also, sets can be combined by operations, similar to operations on numbers.

Sets are a primitive concept, in the sense that it is not possible to define them in terms of more elementary notions, so their study can be done informally, appealing to intuition and logic. On the other hand, with the categories they are one of the fundamental concepts of mathematics: through them (or the categories) the rest of the mathematical objects can be formulated, such as numbers and functions, among others. Its detailed study thus requires the introduction of axioms and leads to set theory.

History of sets

The concept of a set as an abstract object did not begin to be used in mathematics until the 19th century, as doubts about the notion of infinity were dispelled. The works of Bernard Bolzano and Bernhard Riemann already contained ideas related to a vision setter of mathematics. Richard Dedekind's contributions to algebra were formulated in clearly set terms, which are still prevalent in modern mathematics: equivalence relations, partitions, homomorphisms, etc., and he himself made explicit the set-related hypotheses and operations he needed in his work.

Set theory as an independent discipline is usually attributed to Georg Cantor. Beginning with his research on numerical sets, he developed a study on infinite sets and their properties. The influence of Dedekind and Cantor began to be decisive at the end of the XIX century, in the process of «axiomatization» of mathematics, in which all mathematical objects, such as numbers, functions, and various structures, were built on the basis of sets.

Definition

[...] I understand in general by variety or set all multiplicity that can be thought as unity, that is, any collection of certain elements that can be united in a whole by a law.

—Georg Cantor

A set is a well-defined collection of objects, understanding that these objects can be anything: numbers, people, letters, other sets, etc. Some examples are:

A

is the set of smaller natural numbers than 5.

B

is the set of green, white and red colors.

C

is the set of vowels a, e, i, or and u.

D

is the set of the sticks of the French deck.

Sets are usually denoted by capital letters. The objects that make up the set are called elements or members. They are said to "belong" to the set and are denoted by the symbol ∈: the expression $a \in A$ is then read as " $a$ is in $A$ ”, “ $a$ belongs to $A$ ", " $A$ contains $a$ ”, etc. For the opposite notion, the symbol ∉ is used. For example:

3 한 A

Δ 한 D

yellow B

z C

Notation

Membership ratio. The whole

A

It's a set of polygons. In the image, some of the figures belong to that set, but others do not.

There are several ways to refer to a set. In the example above, for the sets $A$ and $D$ , uses an intensive or comprehension definition, where a property is specified that all its elements possess. However, for the sets $B$ and $C$ a extensive definition, listing all its elements explicitly.

It is common to use braces to write the elements of a set, so that:

B = {green, white, red}

C = {a, e, i, o, u}

This brace notation is also used when sets are intensively specified by a property:

A = {Numbers of nature less than 5}

D = {Palos de la baraja française}

Another common notation to denote by comprehension is:

A = m : m is a natural number, and 1 \leq m \leq5}

D = p : p It's a stick in the French deck

F = n 2 : n is an integer and 1 \leq n \leq 10}

In these expressions the colons («:») mean «such that». Thus, the set $F$ is the set of «numbers of the form $n 2$ such that $n$ is an integer between 1 and 10 (both inclusive)”, that is, the set of the first ten squares of natural numbers. Instead of the colon, the vertical bar («|») or oblique «/» is also used.

Equality of sets

Set of people. The set of "persons" shown in the image,

A

You have 8 members. This set can be represented by keys or by a Venn diagram. Order of persons in

A

It's irrelevant.

A set is completely determined by its elements. Therefore, the equality of sets is established as:

Property of extensionality
Two sets $A$ and $B$ that have the same elements are the same set, $A = B$ .

This property has several consequences. The same set can be specified in many different ways, in particular extensive or intensive. For example, the set $A$ of natural numbers less than 5 is the same set as $A'$ , the set of numbers 1, 2, 3 and 4. Also:

B = {green, white, red} = {colors of the Mexican flag}

C = {a, e, i, o, u} = {Spanish vocabulary}

D = {Palos de la baraja française} = {cast, , ♥, ♦}

The order in which the elements are specified is also not taken into account when comparing two sets:

B = {green, white, red} = {red, green, white}

C = {a, e, i, o, u} = {e, i, u, a, o}

Furthermore, an array cannot have "repeating" elements, since an object can only be an element of that array or not. Then, for example:

{1, 2} = {1, 2, 1}

In the absence of some additional distinguishing characteristic of repeated '1's, all that can be said of the set on the right is that '1' is one of its elements.

Empty array

Main article: Vacuum set

The set that contains no element is called the empty set and denotes by $emptyset$ or just {}. Some axiomatic theories of sets ensure that the empty set exists including an axiom of the empty set. In other theories, their existence can be deduced. Many possible properties of assemblies are trivially valid for the empty set.

Properties

In standard axiomatic set theory, by the Axiom of Extensionality, two sets are equal if they have the same elements; therefore there can only be one set without any elements. Consequently, there is only one empty set, and we speak of "the empty set" instead of "an empty set".

For any set A:

(See operations with sets)

The empty set is a subset of A:
${displaystyle forall A:emptyset subseteq A}$
The union of A with the empty set is A:
${displaystyle forall A:Acup emptyset =A}$
The intersection of A with the empty set is the empty set:
${displaystyle forall A:Acap emptyset =emptyset }$
The Cartesian product of A and the empty set is the empty set:
${displaystyle forall A:Atimes emptyset =emptyset }$

The empty set has the following properties:

Its only subset is its own empty set:
${displaystyle forall A:Asubseteq emptyset Rightarrow A=emptyset }$
The power set of the empty set is the set that contains only the empty set:
${displaystyle 2^{emptyset }={emptyset }}$
Its number of elements (cardinality) is zero:
${displaystyle mathrm {n} (emptyset)=0}$

(The list of mathematical symbols used is here).

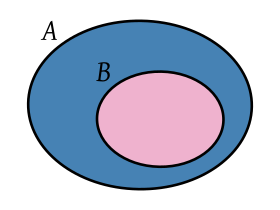
Subsets

Main article: Subset

Subset.

B

is a subset of

A

(in particular a separate subset).

A subset $A$ of a set $B$ , is an array containing some (or perhaps all) of the elements of $B$ :

A set $A$ It's a subset of the whole $B$ if each element of $A$ is in turn an element of $B$ .

When $A$ is a subset of $B$ , it is denoted as $A \subseteq B$ and is said to " $A$ is contained in $B$ ”. You can also write $B \supseteq A$ , and say that $B$ is a superset of $A$ and also " $B$ contains $A$ " or " $B$ includes $A$ ”.

Every set $A$ is a subset of itself, since it is always true that «every element of $A$ is itself an element of $A$ ”. It is common to make a finer distinction using the concept of a proper subset: $A$ is a proper subset of $B$ if it is a subset of $B$ but is not equal to $B$ . It is denoted as $A ⊊ B$ , that is: $A \subseteq B$ but $A \neq B$ (and equivalently, for a proper superset, $B ⊋ A$ ).

Examples.

The “joint of all men” is a subset of the “joint of all people”.

{1,3} {1, 2, 3, 4

{1, 2, 3, 4} {1, 2, 3, 4

Disjoint sets

Main article: Disjunct sets

Two sets $A$ and $B$ are disjoint if not they have nothing in common. For example, the sets of rational numbers and irrational numbers are disjoint: there is no number that is both rational and irrational. The intersection of two disjoint sets is the empty set.

Cardinality

Main article: cardinal number

Sets can be finite or infinite. In the case of a finite set, the elements of the set can be counted:

The number of elements of a finite set is its cardinal.

The cardinal is denoted by $| A |$ , $card(A)$ or $#A$ . Thus, in the previous examples, we have to $| A | = 4$ (four numbers), $| B | = 3$ (three colors) and $| F | = 10$ (ten squares). The only set whose cardinal value is 0 is the empty set $\emptyset$ .

There are, in turn, certain cardinality properties. If we take as an example two sets, A and B:

${displaystyle n(phi)=0}$
${displaystyle A=BRightarrow n(A)=n(B)}$
${displaystyle Asubseteq BRightarrow n(A)leq n(B)}$
${displaystyle n(Acup B)=n(A)+n(B)-n(Acap B)}$
${displaystyle n(U)=n(A)+n(A^{c})}$
${displaystyle n(A-B)=n(A)-n(Acap B)}$

And in the case of three sets, A, B and C:

${displaystyle n(Acup Bcup C)=n(A)+n(B)+n(C)-n(Acap B)-n(Acap C)-n(Bcap C)+n(Acap Bcap C)}$
${displaystyle n(A-(Bcup C))=n(A)-n(Acap B)-n(Acap C)+n(Acap Bcap C)}$
${displaystyle n((Acap B)-C)=n(Acap B)-n(Acap Bcap C)}$
${displaystyle n((Acup B)-C)=n(Acup B)-n(Acap C)-n(Bcap C)+n(Acap Bcap C)}$

In an infinite set there is not a finite number of elements. This is the case, for example, of the natural numbers: $N = {1, 2, 3, \dots}$ . However, there is a way to compare infinite sets with each other, and it turns out that there are infinite sets "bigger" than others. The "number of elements" of an infinite set is a transfinite number.

Cardinality of real numbers

Main article: Actual number

One of the most important results of Georg Cantor was that the cardinality of the real ( ${displaystyle {mathfrak {c}}}$ ) is bigger than that of natural numbers ( $aleph _{0}$ ). This is, there are more real numbers R that integers N. Specifically, Cantor showed that ${aleph _{0}},}" xmlns="http://www.w3.org/1998/Math/MathML">c=2Русский Русский 0▪Русский Русский 0{displaystyle {mathfrak {c}}=2^{aleph _{0}}{aleph _{0}aleph},}{aleph _{0}},}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9bdafb394c3f01d5e356679745d33ac6d0edf735" style="vertical-align: -0.671ex; width:13.194ex; height:3.009ex;"/>$ .

The continuum hypothesis affirms that there are no sets with intermediate cardinality between the natural and the real ones:

There is no set $A$ such that his cardinal $日本語 A 日本語$ fulfill:

<math alttext="{displaystyle aleph _{0}<|A|Русский Русский 0.日本語A日本語.2Русский Русский 0.{displaystyle aleph _{0}. !<img alt="{displaystyle aleph _{0}<|A|

If the axiom of choice is assumed, the structure of infinite cardinals is clearer: all infinite cardinals are alephs and well-ordered, so there is only one cardinal immediately higher than $ℵ 0$ , denoted by $ℵ 1$ . The hypothesis is then equivalent to:

The cardinal of the set of the actual numbers is the immediately superior to the cardinal of the natural numbers:

{displaystyle 2^{aleph _{0}}=aleph _{1}.}

Operations with sets

Joint operations

Union

Intersection

Variance

Complement

Symmetrical difference

Main article: Algebra of sets

There are several basic operations that can be performed, starting from certain given sets, to obtain new sets:

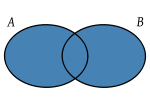
Union(symbol ) The union of two sets $A$ and $B$ represented as $A B$ , is the set of all elements that belong to at least one of the sets $A$ and $B$ .
${displaystyle Acup B={xmid xin Alor xin B}}$
Intersection(symbol ) The intersection of two sets $A$ and $B$ is the whole $A B$ common elements A and B.
${displaystyle Acap B={xmid xin Aland xin B}}$
Variance: (symbol ) The difference of the set $A$ with $B$ is the whole $A B$ resulting from the elimination of $A$ any element that is in $B$ .
${displaystyle Asetminus B={xmid xin Aland xnotin B}}$
Complement: The complement of a set $A$ is the whole $A$ containing all elements that do not belong to $A$ regarding a U set that contains it.
${displaystyle A^{c}={xin Umid xnot in A}}$
Symmetrical difference: (symbol Δ) The symmetrical difference of two sets $A$ and $B$ is the whole $A Δ B$ with all the elements that belong, or $A$ or $B$ But not both at once.
${displaystyle Abigtriangleup B={xmid xin Asetminus Blor xin Bsetminus A}}$
Cartesian product: (symbol ×) The Cartesian product of two sets $A$ and $B$ is the whole $A \times B$ of all pairs ordained $(a, b)$ formed with a first element $a$ of $A$ and a second element $b$ of $B$ .

Examples

${1} a 0! {2. b *** b, 1, a 0!$
${5, z, ё} {castle, a} = {cast}$
${5, z, Catalog} {cast, a *** z!$
${Guide, 5} Δ {8, #, γ} = {5, #, 8}$
${1} a, 0} \times {2, b} = {(1, 2), (1, b), (a (2), (a, b), (0, 2), (0, b!$

Contenido relacionado

Más resultados...