Scale (mapping)
The scale is the proportion between the real dimensions of an object and those of the drawing that represents it. For example, if a scale indicates a ratio of 1:15,000, it means that one centimeter on the map represents 15,000 cm in the real world.
The first form is the relationship between the size of the generating balloon and the size of the Earth. The generator globe is a conceptual model to which the Earth is reduced and from which the map is projected. The ratio between the size of the Earth and that of the generating globe is called the nominal scale (= major scale = representative fraction). Many maps indicate nominal scale and may even show a bar scale (sometimes just called scale) to represent it.
The second distinct concept of scale applies to the variation of scale on a map. It is the relationship between the scale of the mapped point and the nominal scale. In this case 'scale' means the scale factor (= point scale = particular scale).
If the map region is small enough to ignore the curvature of the Earth, as in the case of a city plan, a single value can be used as a scale without causing measurement error. On maps that cover larger areas, or the entire Earth, the map scale may be less useful or even useless for measuring distances. Map projection becomes critical to understanding how scale varies across the map. When scale varies markedly, the scale factor can be accounted for. The Tissot indicatrix is often used to illustrate the variation of the scale of points on a map.
History
The foundations of quantitative map scaling date back to ancient China, with textual evidence that the idea of map scaling was understood as early as the 17th century II a. C. The ancient Chinese surveyors and cartographers had extensive technical resources for making maps, such as counting rods, a carpenter's square, a plumb bob, compasses to draw circles, and sight tubes to measure inclination. Reference frames that postulated an incipient coordinate system to identify places were hinted at by ancient Chinese astronomers who divided the sky into various lunar sectors or lodges.
Chinese cartographer and geographer Pei Xiu of the Three Kingdoms period created a set of large-area maps that were drawn to scale. He developed a set of principles that emphasized the importance of consistency of scale, directional measurements, and adjustments to the measurements of the terrain being mapped.
Types of scales
There are three types of scales:
- Natural scale: It is when the size of the object represented on the plane coincides with reality. There are several standardized flat formats to try to occupy reduction spaces.
- Reduction scale: It is used when the physical size of the plane is less than reality. This scale is used to represent parts (E.1:2 or E.1:5), housing plans (E:1:50), physical maps of territories where the reduction is much greater and can be scales of the order of E.1:50.000 or E.1:100.000.
- Scale of expansion: It is used when making the plane of very small pieces or details of a plane. In this case the value of the numerator is higher than the value of the denominator, or it should be divided by the numerator to know the actual value of the piece.
Large-scale maps without taking curvature into account
The region in which the earth can be considered flat depends on the precision of survey measurements. If measured to the nearest meter only, then the curvature of the earth is undetectable at a meridian distance of about 100 kilometers (62.1 mi) and on an east-west line of about 80 km (at 45 degree latitude). If measured to the nearest 1 millimeter (0 in), the curvature is undetectable on a meridian of about 10 km and on an east-west line of about 8 km. Thus, a map of New York City with a precision of one meter or a plan of a work with a precision of one millimeter would both satisfy the previous conditions for the disregard of curvature. They can be dealt with by planar topography and can be mapped by scale drawings in which any two points at the same distance on the drawing are at the same distance on the ground. True ground distances are calculated by measuring the distance on the map and then multiplying by the inverse of the scale fraction or, equivalently, simply using divisors to transfer the spacing between map points to a scale bar on the map. Map.
Point scale (or particular scale)
As demonstrated in Gauss's Theorema egregium, a sphere (or ellipsoid) cannot be projected onto a plane without being deformed. This is commonly illustrated by the impossibility of smoothing an orange peel on a flat surface without breaking and deforming it. The only real representation of a sphere at constant scale is another sphere such as a globe.
Given the limited practical size of globes, we must use maps for detailed mapping. Maps require projections. A projection implies a distortion: A constant separation on the map does not correspond to a constant separation on the ground. Although a map may display a bar graph scale, the scale should be used with the understanding that it will only be accurate to some lines on the map. (This is discussed in more detail in the examples in the following sections.)
Sea P a point of latitude φ φ {displaystyle varphi } and length λ λ {displaystyle lambda } in the sphere (or ellipsoid). Be Q a neighboring point and be α α {displaystyle alpha } the angle between the PQ and the meridian element in P: this angle is the angle acimut of the PQ element. Sean P' and Q' the corresponding points of the projection. The angle between the P'Q' address and the meridian projection is the to β β {displaystyle beta }. In general, alfa{displaystyle alfa}. Commentary: this precise distinction between the acimuth (on the surface of the Earth) and the course (on the map) is not universally observed, since many writers use the terms almost indistinctly.
Definition: the point scale in P is the ratio of the two distances P'Q' and PQ in the limit where Q approaches P. We write it as
- μ μ (λ λ ,φ φ ,α α )=limQ→ → PP♫Q♫PQ,{displaystyle mu (lambda,varphi,alpha)=lim _{Qto P}{frac {P'Q'}{PQ}}},} where notation indicates that the point scale is function of the P position and also of the PQ element direction.
Definition: if P and Q are in the same meridian (α α =0){displaystyle (alpha =0)}, the Meridian scale denotes by h(λ λ ,φ φ ){displaystyle h(lambda,varphi)}.
Definition: if P and Q are in the same parallel (α α =π π /2){displaystyle (alpha =pi /2)}, the parallel scale denotes by k(λ λ ,φ φ ){displaystyle k(lambda,varphi)}.
Definition: if the point scale depends only on the position, not the direction, it is said that it is is isotropic and conventionally denotes its value in any direction by the parallel scale factor k(λ λ ,φ φ ){displaystyle k(lambdavarphi)}.
Definition: A map projection is said to be conformal if the angle between a pair of intersecting lines at a point P is the same as the angle between the lines projected at the projected point P& #39;, for all pairs of lines that intersect at point P. A conformal map has an isotropic scale factor. Conversely, isotropic scale factors across the map imply a conformal projection.
Isotropy of scale implies that small elements are stretched equally in all directions, ie the shape of a small element is preserved. This is the property of orthomorphism, from the Greek meaning “correct form”. The qualifier small means that with a given measurement precision no change in the scale factor on the element can be detected. Since conformal projections have an isotropic scale factor, they have also been called orthomorphic projections. For example, the Mercator projection is conformal in that it is constructed to preserve angles and its scale factor is isotropic, a function of latitude only: Mercator does preserve shape in small regions.
Definition: In a projection conforming to an isotropic scale, points that have the same scale value can be joined to form isoscale lines. These are not plotted on the maps for end users, but appear in many of the standard texts. (See Snyder pages 203-206.)
The Representative Fraction (RF) or Major Scale
There are two conventions used to establish the equations of any projection. For example, the equirectangular cylindrical projection can be written as
- cartographers: x=aλ λ {displaystyle x=alambda } and=aφ φ {displaystyle and=avarphi }
- mathematicians: x=λ λ {displaystyle x=lambda } and=varphi{displaystyle y=varphi}
Here we will adopt the first of these conventions (following the usage in Snyder's studios). It is evident that the above projection equations define positions in a huge cylinder wrapped around the Earth and then unrolled. These coordinates are said to define the projection map that should be logically distinguished from actual printed (or seen) maps. If the definition of the point scale in the previous section is in terms of the projection map, then we can expect the scale factors to be close to unity. For normal tangent cylindrical projections, the scale along the equator is k=1 and, in general, the scale changes as we move further from the equator. Analysis of the scale in the projection map is an investigation of the change of k away from its true value of unity.
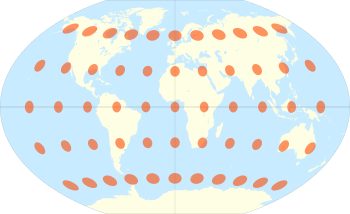
Display of the dotted scale: the Tissot indicatrix
Consider a small circle on Earth's surface centered on a P point in latitude φ φ {displaystyle varphi } and length λ λ {displaystyle lambda }. As the point scale varies with position and direction, the circle projection over the projection will be distorted. Tissot showed that, whenever the distortion is not too large, the circle will become an ellipse on the projection. In general, the dimension, shape and orientation of the ellipse will change over the projection. The overlap of these distortion ellipses on the projection of the map conveys the way the dot scale changes on the map. The distortion ellipse is known as Tissot's signal. The example shown here is the projection of Winkel-Tripel, the standard projection for the world maps made by the National Geographic Society. The minimum distortion occurs in the central meridian to latitudes of 30 degrees (North and South). (Other examples).
The terminology of scales
Scale of representation
Map scales can be expressed in words (a lexical scale), as a ratio, or as a fraction. Some examples are:
- 'one centimeter a hundred meters' or 1:10,000 or 1/10,000
- 'an inch at a mile' or 1:63,360 or 1/63,360
- 'one centimeter a thousand kilometers' or 1:100,000,000 or 1/100,000,000. (The ratio would generally be abbreviated to 1: 100M)
Bar scale vs. lexical scale
In addition to the above, many maps carry one or more bar (graph) scales. For example, some modern British maps have three bar scales, one each for kilometers, miles, and nautical miles.
A lexical scale in a language known to the user that may be easier to visualize than a ratio: if the scale is from one inch to two miles and the map user can see two villages that are about two inches apart distance on the map, then it's easy to figure out which villages are about four miles apart on the ground.
A lexical scale can cause problems if it is expressed in a language that the user does not understand or in obsolete or poorly defined units. For example, many older people will understand a scale from one inch to one furlong (1:7920) in countries where imperial units used to be taught in schools. But a scale from a pouce to a league may be about 1:144,000, depending on the cartographer's choice of the many possible definitions for a league, and only a minority of modern users will be familiar with the units used.
Large scale, medium scale, small scale
Contrast with spatial scale. A map is classified as small or large scale or sometimes medium. Small scale refers to world maps or maps of large regions, such as continents or large nations. In other words, they show large areas of land in a small space. They are called small scale because the representative fraction is relatively small.
Large-scale maps show smaller areas in more detail, like county maps or city plans. These maps are called large-scale because the representative fraction is relatively large. For example, a city plan, which is a large-scale map, might be at a scale of 1:10,000, while a world map, which is a small-scale map, might be at a scale of 1: 100,000,000.
The following table describes typical ranges for these scales, but should not be considered authoritative because there is no standard:
| Classification | Rank | Examples |
|---|---|---|
| Large scale | 1:0 – 1:600,000 | 1:0,00001 map of a virus; 1:5000 pedestrian map of a town |
| Medium scale | 1:600,000 – 1:2,000.000 | Country map |
| Small scale | 1:2,000.000 - 1: | 1:500,000 for the world map; 1:1021 for the map of the galaxy |
Sometimes the terms are used in the absolute sense of the table, but at other times they are used in a relative sense. For example, a map reader whose work concentrates exclusively on large-scale maps (as indicated in the table above) might refer to a 1:500,000 scale map as small-scale.
Contenido relacionado
Miahuatlan by Porfirio Diaz
Araucania region
Cylindrical projection