Scalar product

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Representation of the climbing product in the eucliding space.

In mathematics, the dot product, also known as the inner product or dot product, is an algebraic operation that takes two vectors and returns a scalar, y which satisfies certain conditions.

Of all the products that can be defined in different vector spaces, the most relevant is the so-called "scaler" (usual or standard) in the euclid space $mathbb {R} ^{n}$ . Given two vectors u ${displaystyle =(u_{1},u_{2},...,u_{n})}$ and v ${displaystyle =(v_{1},v_{2},...,v_{n})}$ , his product scale defined as

cdot

{displaystyle =u_{1}cdot v_{1}+u_{2}cdot v_{2}+...+u_{n}cdot v_{n}}

that is, the sum of the component-by-component products. This expression is equivalent to the matrix product of a row matrix and a column matrix, so the usual scalar product can also be written as

cdot

v = u

{displaystyle ^{T}}

where the agreement to write the vectors in column and u ${displaystyle ^{T}}$ represents the transition u.

The numerical value of the scalar product is equal to the product of the modules of the two vectors and the cosine of the angle between them, which allows us to use the scalar product to study typical concepts of Euclidean geometry in two and three dimensions, such as lengths, angles and orthogonality. The scalar product can also be defined in Euclidean spaces with a dimension greater than three, and in general in real and complex vector spaces, to which these same geometric concepts can be transferred. Vector spaces endowed with an inner product are called pre-Hilbert spaces.

The name of the dot product is derived from the symbol used to denote this operation (« »). The name dot product emphasizes the fact that the result is a scalar rather than a vector, unlike for example the vector product. Both denominations are usually reserved for the usual scalar product, while in the general case the use of the expression internal product is more frequent.

General definition

In a vector space, an inner product is a map

{displaystyle {begin{array}{rccl}langle cdotcdot rangle:&Vtimes V&longrightarrow &mathbb {K} \&(x,y)&longmapsto &a=langle x,yrangle end{array}}}

where $V$ It's a vector space. ${mathbb {K}}$ the body on which it is defined. The binary operation $langle cdot,cdot rangle$ (which takes as arguments two elements of $V ;$ and returns an element of the body ${mathbb {K}}$ ) must satisfy the following conditions:

Linearity on the left: $langle ax+by,z rangle = a langle x,z rangle + b langle y,z rangle$ , and linearity conjugated by the right: $langle x, ay+bz rangle = overline{a} langle x, y rangle + overline{b} langle x,z rangle$ .
Hermiticity: $langle x,y rangle = overline{langle y,x rangle}$ .
Positive defined: $langle x,x rangle geq 0 ,$ and $langle x,x rangle = 0 ,$ Yes and only if x = 0,

where $x, y, z in V$ They're vectors, $a, b in mathbb{K}$ They're climbers, and $overline{c}$ is the conjugate of the complex scaler c.

Consequently, an internal product defined in a vector space is a form sesquilineal, hermitic and positive defined. If the underlying body ${mathbb {K}}$ has a null imaginary part (e.g., $mathbb{R}$ ), the property of being sesquilineal becomes bilineal and the hermitic being becomes symmetrical. Therefore, in a real vector space, an inner product is a positive defined bilineal shape.

Alternatively, the operation is usually represented by the point symbol ( $cdot$ ), with what the product of the vectors ${displaystyle {bf {u}}}$ and ${displaystyle {bf {v}}}$ represented as ${displaystyle {bf {{u}cdot {bf {v}}}}}$ .

A vector space on the body $mathbb{R}$ or $mathbb{C}$ endowed with an internal product is called prehilbert space, prehilbert space or unit space. If it is also complete, it is said to be a space of Hilbert. If the dimension is finite and the body is that of the actual numbers, it will be said that it is an euclid space.

Every inner product induces a quadratic form, which is positive definite, and is given by the product of a vector with itself. Likewise, it induces a vector norm as follows:

$| x |:= sqrt{langle x,x rangle}$

that is, the norm of a vector is the square root of the image of that vector in the associated quadratic form.

Inner Product Examples

The following is a list of some products generally studied in the theory of pre-Hilbertian spaces. All these products —called canonical— are just some of the infinite interior products that can be defined in their respective spaces.

In the vector space $mathbb {R} ^{n}$ the interior product is usually defined (called, in this particular case, product point) by:

{displaystyle mathbf {A} cdot mathbf {B} =(a_{1},a_{2},a_{3},...,a_{n})cdot (b_{1},b_{2},b_{3},...,b_{n})=a_{1}b_{1}+a_{2}b_{2}+...a_{n}b_{n}=sum a_{i}cdot b_{i}}

In the vector space $mathbb{C}^n$ the interior product is usually defined by:

mathbf{A}cdotmathbf{B}=(a_1, a_2, a_3,..., a_n)cdot(b_1,b_2,b_3,..., b_n)=a_1 overline{b_1} + a_2 overline{b_2} +... a_n cdot overline{b_n} = sum a_i cdot overline{b_i}

where

overline{b_n}

is the complex conjugate number of

b_n

In the vector space of the matrices m x nwith real tickets

mathbf{A}cdotmathbf{B}=operatorname{tr} (A^T cdot B)

where tr(M) is the trace of the M matrix and

A^T

is the transposed matrix of A.

In the vector space of the matrices m x n with complex inputs

mathbf{A}cdotmathbf{B}=operatorname{tr} (A^* cdot B)

where tr(M) is the trace of the M matrix and

A^*

is the transposed conjugate matrix of A.

In the vector space of the continuous complex functions in the interval a and b, denoted by ${displaystyle {mathcal {C}}[a,b]}$ :

mathbf{f}cdotmathbf{g} = int_{a}^{b} f(x)overline{g(x)}mathrm{d} x

In the vector space of polynomials less or equal to n, dice n+1 numbers $textstyle [x_1,x_2,x_3,...,x_n,x_{n+1}] subseteq mathbb{R}$ such that $<math alttext="{displaystyle textstyle x_{1}<x_{2}<x_{3}<...<x_{n}x1.x2.x3.....xn.xn+1{displaystyle textstyle x_{1} visx_{2} visx_{3} inherent...<img alt="{displaystyle textstyle x_{1}<x_{2}<x_{3}<...<x_{n}$ :

{displaystyle mathbf {p} cdot mathbf {q} =p(x_{1})q(x_{1})+p(x_{2})q(x_{2})+...+p(x_{n})q(x_{n})+p(x_{n+1})q(x_{n+1})=sum p(x_{i})cdot q(x_{i})}

Inner Product Properties

Sean A, B and C vectors, and be $alpha$ and $beta$ scales:

It is a linear application for the first operation:

${displaystyle langle alpha mathbf {A} +beta mathbf {B}mathbf {C} rangle =alpha langle mathbf {A} cdot mathbf {C} rangle +beta langle mathbf {B} cdot mathbf {C} rangle }$

It's a hermitian form:

${displaystyle langle mathbf {A}mathbf {B} rangle ={overline {langle mathbf {B}mathbf {A} rangle }}.}$

In a real vector space, this condition is reduced to

${displaystyle mathbf {A} cdot mathbf {B} =mathbf {B} cdot mathbf {A}}$

so in this case the internal product is commutative (or symmetrical).

The two previous combined properties siginify that the interior product is sesquilineal:

${displaystyle langle mathbf {A}alpha mathbf {B} +beta mathbf {C} rangle ={overline {alpha }}langle mathbf {A} cdot mathbf {B} rangle +{overline {beta }}langle mathbf {A} cdot mathbf {C} rangle }$

again, in the real case, this property is reduced to linearity in the second operating.

Distribution with respect to the sum:

${displaystyle langle mathbf {A}mathbf {B} +mathbf {C} rangle =langle mathbf {A}mathbf {B} rangle +langle mathbf {A}mathbf {C} rangle }$

${displaystyle langle mathbf {A} +mathbf {B}mathbf {C} rangle =langle mathbf {A}mathbf {C} rangle +langle mathbf {B}mathbf {C} rangle }$

Possivity: in real or complex vector spaces, the internal product of a vector itself is a non-negative real number:

${displaystyle langle mathbf {A}mathbf {A} rangle geq 0.}$

Consequently, it is possible to define a vector standard of value ${displaystyle ||mathbf {A} ||={sqrt {langle mathbf {A}mathbf {A} rangle }}}$ which is defined for all the vectors of space and fulfills all the required axioms. Therefore, every prehilbertian space is a standard space. In the usual climbing product, the associated standard equals the length of the vector in the euclid space.

Cauchy-Bunyakovsky-Schwarz:

${displaystyle |langle mathbf {A}mathbf {B} rangle |leq ||mathbf {A} ||cdot ||mathbf {B} ||.}$

As a result, for two non-null vectors A and B have the inequalities:

${displaystyle -1leq {frac {langle mathbf {A}mathbf {B} rangle }{||mathbf {A} ||cdot ||mathbf {B} ||}}leq 1.}$

In the usual climbing product, this quotient is equal to the angle cosine between the two vectors. This leads to defining the concept of angle in arbitrary vector spaces as the angle $theta$ such as

${displaystyle cos theta ={frac {langle mathbf {A}mathbf {B} rangle }{||mathbf {A} ||cdot ||mathbf {B} ||}}.}$

The usual dot product in real Euclidean space

Analytic expression

Be vectors U ${displaystyle =(U_{1},U_{2},U_{3})^{T}}$ and V ${displaystyle =(V_{1},V_{2},V_{3})^{T}}$ in the three-dimensional eucliding space ${mathbb {R}}^{3}$ . The climbing product U and V is defined as the matrix product:

${displaystyle mathbf {U} cdot mathbf {V} =U^{T}V={begin{bmatrix}U_{1}&U_{2}&U_{3}\end{bmatrix}}{begin{bmatrix}V_{1}\V_{2}\V_{3}\end{bmatrix}}=U_{1}V_{1}+U_{2}V_{2}+U_{3}V_{3},}$

If the vectors are expressed through their coordinates regarding a certain base ${displaystyle {mathcal {B}}={e_{1},e_{2},e_{3}}}$ , by application of the properties of the climbing product, this takes the form

${displaystyle mathbf {U} cdot mathbf {V} }$	$~=$	${displaystyle (u_{1}mathbf {e} _{1}+u_{2}mathbf {e} _{2}+u_{3}mathbf {e} _{3})cdot (v_{1}mathbf {e} _{1}+v_{2}mathbf {e} _{2}+v_{3}mathbf {e} _{3})}$
	$~=$	${displaystyle {begin{matrix}u_{1}v_{1}mathbf {e} _{1}cdot mathbf {e} _{1}+u_{2}v_{1}mathbf {e} _{2}cdot mathbf {e} _{1}+u_{3}v_{1}mathbf {e} _{3}cdot mathbf {e} _{1}\+u_{1}v_{2}mathbf {e} _{1}cdot mathbf {e} _{2}+u_{2}v_{2}mathbf {e} _{2}cdot mathbf {e} _{2}+u_{3}v_{2}mathbf {e} _{3}cdot mathbf {e} _{2}\+u_{1}v_{3}mathbf {e} _{1}cdot mathbf {e} _{3}+u_{2}v_{3}mathbf {e} _{2}cdot mathbf {e} _{3}+u_{3}v_{3}mathbf {e} _{3}cdot mathbf {e} _{3}end{matrix}}}$

The above expression can be condensed in matrix form as

${displaystyle mathbf {U} cdot mathbf {V} ={begin{bmatrix}u_{1}&u_{2}&u_{3}\end{bmatrix}}{begin{bmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}\end{bmatrix}}{begin{bmatrix}v_{1}\v_{2}\v_{3}\end{bmatrix}}=U_{mathcal {B}}^{T}AV_{mathcal {B}},}$

where A is the Gram matrix of the product, whose entries are the scale products of the base vectors: ${displaystyle a_{ij}=e_{i}cdot e_{j}}$ . In the particular case that the base is orthonormal, the Gram matrix is the identity matrix.

Previous expressions can be generalized to spaces of n dimensions. Yeah. U and V are vectors in $mathbb {R} ^{n}$ Then:

${displaystyle mathbf {U} cdot mathbf {V} =U_{1}V_{1}+U_{2}V_{2}+...+U_{n}V_{n}.}$

Similarly, given the coordinates of the vectors regarding a base ${displaystyle {mathcal {B}}={e_{1},e_{2},...,e_{n}}}$ , the product is given by

${displaystyle mathbf {U} cdot mathbf {V} =U_{mathcal {B}}^{T} A V_{mathcal {B}},}$

where the Gram matrix A is of order n x n.

Vector modulus

Main article: Module (vector)

The dot product of a vector with itself is equal to the sum of the squares of its components:

${displaystyle mathbf {U} cdot mathbf {U} =U_{1}^{2}+U_{2}^{2}+...+U_{n}^{2}.}$

Since it is a sum of squares, all the addends are non-negative, and it is only zero when all the components are zero, that is, when U is the null vector. Otherwise it is a positive real number that, by successive application of the Pythagorean theorem, is equal to the square of the distance between the origin of coordinates and the extreme point of the vector U. In summary:

${displaystyle mathbf {U} cdot mathbf {U} =||U||^{2},}$

In other words, the magnitude (or norm) of the vector U is the square root of the scalar product of U with itself.

A module vector equal to the unit is called a unit vector, and it is usually denoted with a circumflex accent, as ${displaystyle {hat {u}}}$ . It is always possible to obtain a unitary vector in the direction of any non-null vector vmultiplying it by the reverse of its rule. This process is called normalization of the vector v.

Angle between two vectors

Triangle defined by two vectors u and v.

Applying the cosine theorem to the triangle defined by two vectors u and v, we have that

${displaystyle ||mathbf {v} -mathbf {u} ||^{2}=||mathbf {u} ||^{2}+||mathbf {v} ||^{2}-2cdot ||mathbf {u} ||cdot ||mathbf {v} ||cdot cos theta }$

which can be rewritten as

${displaystyle 2cdot ||mathbf {u} ||cdot ||mathbf {v} ||cdot cos theta =||mathbf {u} ||^{2}+||mathbf {v} ||^{2}-||mathbf {v} -mathbf {u} ||^{2}.}$

The square of the norm of each of these vectors is:

${displaystyle ||mathbf {u} ||^{2}=mathbf {u} cdot mathbf {u} =u_{1}^{2}+u_{2}^{2}+...+u_{n}^{2}.}$

${displaystyle ||mathbf {v} ||^{2}=mathbf {v} cdot mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.}$

${displaystyle ||mathbf {v} -mathbf {u} ||^{2}=(mathbf {v-u})cdot (mathbf {v-u})=(v_{1}-u_{1})^{2}+(v_{2}-u_{2})^{2}+...+(v_{n}-u_{n})^{2}.}$

Substituting in the previous expression, and since ${displaystyle (v_{i}-u_{i})^{2}=v_{i}^{2}-2u_{i}v_{i}+u_{i}^{2}}$ after canceling all the sums the way ${displaystyle u_{i}^{2}}$ and ${displaystyle v_{i}^{2}}$ Just stay.

${displaystyle 2cdot ||mathbf {u} ||cdot ||mathbf {v} ||cdot cos theta =2u_{1}v_{1}+2u_{2}v_{2}+...+2u_{n}v_{n}=2 mathbf {u} cdot mathbf {v} }$

from where, if the norm of both vectors is non-zero, we can solve for

${displaystyle cos theta ={frac {mathbf {u} cdot mathbf {v} }{||mathbf {u} ||cdot ||mathbf {v} ||}} ={frac {mathbf {u} cdot mathbf {v} }{{sqrt {mathbf {u} cdot mathbf {u} }}{sqrt {mathbf {v} cdot mathbf {v} }}}}.}$

The denominator of this expression is always positive, so the sign of the climbing product coincides with that of the angle cosine $theta$ . The climbing product is positive when this angle is less than the right angle, and it is negative when the angle is greater.

Geometric definition

A • B =.A日本語BΔ cos(θ).
日本語AΔ cos(θ) is the scale projection of A in B.

The above expression for the cosine of the angle between the vectors can be used to give an alternative definition of the dot product. This definition of a geometric character is independent of the chosen coordinate system and therefore of the chosen basis of the vector space. However, it is equivalent to the analytical definition given above, given in terms of the components of these vectors.

The two vector scaling product in an euclid space, usually denoted ${displaystyle mathbf {A} cdot mathbf {B} }$ , is geometrically defined as the product of its modules by the angle cosine $theta$ That they form.

$mathbf{A} cdot mathbf{B}= |mathbf{A}| |mathbf{B}| cos theta = A ,B ,cos theta$

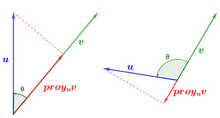
Projection of one vector onto another

Projection

The orthogonal projection of a vector u onto (the direction of) a vector v, other than the null vector, is defined as the vector parallel to v that results from projecting u onto the subspace spanned by v. In other words, it is the shadow that one vector casts on the other.

The vector projection module u on the direction of the vector v That's it. ${displaystyle ||P_{v}(u)||=||u||costheta }$ with which

${displaystyle mathbf {u} cdot mathbf {v} =||P_{v}(u)||cdot ||v||}$

that is, the scalar product of two vectors can also be defined as the product of the magnitude of one of them by the projection of the other onto it.

Consequently, the projection can be calculated as the dot product between both vectors, divided by the magnitude of the vector v squared, multiplied by the vector v:

{displaystyle P_{v}(u)={frac {langle {bf {{u},{bf {{v}rangle }}}}}{||{bf {{v}||}}}}cdot {frac {bf {v}}{||{bf {{v}||}}}}={frac {langle {bf {{u},{bf {{v}rangle }}}}}{langle {bf {{v},{bf {{v}rangle }}}}}}{bf {v}}}

For example, in the case of Euclidean space in two dimensions, the projection of the vector u=(4, 5) onto the vector v= (5, - 2) is the vector

{displaystyle P_{v}(u)={frac {4cdot 5+5cdot (-2)}{5^{2}+(-2)^{2}}}(5,-2)=(50/29,-20/29).}

In the particular case that the direction of a unit vector e is considered, the expression for the projection of a vector u onto e > takes the simplified form

${displaystyle P_{e}(u)=langle {bf {{u},{bf {{e}rangle {bf {e}}}}}}}$ .

The above expressions are used in the Gram-Schimdt method to obtain an orthonormal basis.

Orthogonal Vectors

Two vectors are orthogonal or perpendicular when they form a right angle to each other. If the dot product of two vectors is zero, then both vectors are orthogonal.

${displaystyle mathbf {A} cdot mathbf {B} =0qquad Leftrightarrow qquad mathbf {A} bot mathbf {B} }$

since the $cosfrac{pi}{2} = 0$ .

Vectors parallel or in the same direction

Two vectors are parallel or have the same direction if the angle they make is 0 radians (0 degrees) or π radians (180 degrees).

When two vectors form a zero angle, the value of the cosine is unity, therefore the product of the modules is equal to the scalar product.

${displaystyle mathbf {A} cdot mathbf {B} =A,B,cos theta quad &quad |mathbf {A} cdot mathbf {B} |=|A|,|B|leftrightarrow |cos theta |=1leftrightarrow A||B}$

Generalizations

Quadratic forms

Given a symmetrical bilinear shape $scriptstyle B(cdot,cdot)$ defined on a vector space $scriptstyle V = R^n$ a different climbing product can be defined using the formula:

${displaystyle (mathbf {u}mathbf {v})_{B}={begin{bmatrix}u_{1}&dots &u_{n}end{bmatrix}}{begin{bmatrix}B_{11}&dots &B_{1n}\dots &dots &dots \B_{n1}&dots &B_{nn}end{bmatrix}}{begin{bmatrix}v_{1}\dots \v_{n}end{bmatrix}}=sum _{i=1}^{n}sum _{j=1}^{n}B_{ij}u_{i}v_{j}}$

Where:

B_{ij}:= B(mathbf{e}_i,mathbf{e}_j)

{ mathbf{e}_1, dots, mathbf{e}_n }

is a base of the vector space

scriptstyle V

It can be verified that the previous operation $scriptstyle (cdot,cdot)_B:Vtimes V to R$ satisfies all properties to satisfy a climbing product.

Metric Tensioners

You can define and handle non-euclid space or more exactly Riemann varieties, that is, non-plane spaces with a different curvature tensor of zero, in which we can also define lengths, angles and volumes. In these more general spaces the concept of geodesic is adopted instead of that of segment to define the shortest distances in between points and, also, the operative definition of the usual climbing product is slightly modified by introducing a metric tensioner $scriptstyle g:mathcal{M}times Tmathcal{M} times Tmathcal{M} to R$ such that the limiting of the tensor to a point of the Riemann variety is a bilineal form $scriptstyle g_x(cdot,cdot) = g(x;cdot,cdot)$ .

So, given two vectors vector fields ${displaystyle mathbf {u} }$ and ${mathbf {v}}$ from tangent space to the Riemann variety is defined your internal product or scaling as:

${displaystyle langle mathbf {u}mathbf {v} rangle =g_{x}(mathbf {u}mathbf {v})=sum _{i}sum _{j}g_{ij}(x)u_{i}v_{j}}$

The length of a rectifying curve C between two points A and B can be defined from its tangent vector ${displaystyle scriptstyle mathbf {T} }$ as follows:

${displaystyle L_{C}=int _{s_{a}}^{s_{b}}{sqrt {g(mathbf {x}mathbf {T}mathbf {T})}} ds=int _{s_{a}}^{s_{b}}{sqrt {g_{ij}{frac {dx^{i}}{ds}}{frac {dx^{i}}{ds}}}} ds}$

Contenido relacionado

Más resultados...