Rounding
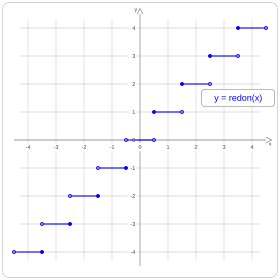
Rounding is the process of dropping digits in the decimal (or more generally, positional) expression of a number. It is used in order to facilitate calculations or to avoid giving the impression that a value is known with greater accuracy than it really is. Approximations are generally symbolized by ≈ (U+2248), including rounding. For example: √2 ≈ 1.414. The figure on the right represents the rounding function to an integer.
When intermediate values are rounded in a calculation, rounding errors typically accumulate which can cause the result thus obtained to vary significantly from the result of the exact calculation.
Standard rounding method
For rounding, whatever the method, the number of digits to be kept must be stated in advance.
The method recommended by NIST and ISO can be described with 2 rules:
- Choose the nearest number that has the number of significant digits chosen.
- If there are two equal numbers of nearby, you choose the one that has as last significant digit a pair number (multiple of 2).
| Number Original | Digits to preserve | Outcome | Notes |
|---|---|---|---|
| 13.95 | 2 | 14 | 14 is closer than 13. |
| 13.95 | 3 | 14.0 | 13.95 is equal to about 14.0 and 13.9 so choose the one that has the last significant digit to -the 0-. |
| 22 805 | 2 | 23 000 | 22 805 is closer to 23 000 than 22 000 |
| 22 805 | 3 | 22 800 | 22 805 is closer to 22 800 than 22 900 |
| 22 805 | 4 | 22 800 | 22 805 is equal to about 22 800 and 22 810 so choose the one that has the last significant digit pair. |
Arithmetic operations
- In multiplications, divisions and powers, the final result will have the same number of significant figures as the factor with the least significant figures. For example:
- 84.25× × 22.3=1878.775≈ ≈ 1.88× × 103{displaystyle 84.25times 22.3=1~878.775approx 1.88times 10^{3}}
Contenido relacionado
Necessary condition
Hamiltonian
De Rham cohomology