Rotatory motion

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Earth Rotation.

Rotation is the movement of changing the orientation of a body or a reference system so that a line (called axis of rotation) or a point remains fixed.

The rotation of a body is represented by an operator that affects a set of points or vectors. The rotary movement is represented by the vector angular velocity ${boldsymbol omega }$ , which is a slider and placed on the rotation axis. When the axis passes through the center of mass or gravity it is said that the body "turns over itself".

Rotation can also be oscillatory, as in the pendulum (Left). The spins are complete only when the energy is high enough (Right.). The upper graph shows the trajectory in the phase space.

In mechanical engineering, a revolution is called a complete rotation of a part about its axis (as in the unit revolutions per minute), while in astronomy it is use this same word to refer to the orbital movement of translation of a body around another (like the planets around the Sun).

Rotation in physics

Concept of rotation and revolution

Animation of two objects orbiting around a common mass center, an example of revolution.

Example of rotation.

Example of revolution.

The movement of the structure of a noria corresponds to a rotation movement. On the contrary, the noria barks make a movement of translation or revolution with a circular trajectory.

In astronomy it is usual to distinguish between the movement of rotation and that of revolution with the following meanings:

La rotation of a body around an axis (exterior or interior to the body) corresponds to a movement in which the different points of the body present speeds that are proportional to its distance to the axis. The points of the body located on the axis (in the event that it is inside the body) remain at rest.
- The orientation of the body in space changes continuously during the translation.
- An example of rotation is that of the Earth around its own axis of rotation, with a period of rotation of a Side day.
La Revolution of a particle or an extensive body corresponds to a transfer movement of the body around another.

- An example of revolution is that of the Earth around the Sun, with a period of revolution of one year.

The distinction between rotation and revolution is associated with that between rotation and translation of an extended body. If the translation speed is constant (v=cte), each of the points of the solid will travel a rectilinear trajectory with constant speed and all these trajectories will be parallel to each other (uniform translation movement). But, in general, the translation speed does not have to be constant and the trajectory can be curvilinear.

The trajectories covered by the different points of the body can be circles, all of them with the same radius (congruent), although with different centers. This situation occurs in a fairground wheel with a horizontal axis, as shown in the figure: the frame of the wheel rotates around the axis (rotation), but the gondolas suspended from said frame, regardless of small pendulum oscillations, experience a translation with circular trajectories.

Rotary movement

Main article: Rotary movement

Infinitesimal rotation

In a rotation through an infinitesimal angle δθ, one can take cos δθ ≈ 1 and sin δθ ≈ δθ, so that the expression for the plane rotation becomes:

${displaystyle mathbf {r} '=mathbf {r} +delta theta (mathbf {u} times mathbf {r})}$

If two infinitesimal rotations are composed and, therefore, the terms of order higher than the first are discarded, it is verified that they possess the commutative property, which finite three-dimensional rotations do not.

Mathematically the set of infinitesimal rotations in the euclid space form the Lie algebra ${displaystyle {mathfrak {so}}(3)}$ associated with the Lie SO(3) group

Angular velocity

Main article: Filmmatic of rigid solid

Given a rigid body that rotates about an axis, the linear velocity v of a particle can be expressed from the angular velocity ω:

${displaystyle mathbf {v} ={frac {dmathbf {r} }{dt}}={boldsymbol {omega }}times mathbf {r} }$

While the acceleration a is:

${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={boldsymbol {alpha }}times mathbf {r} +{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r})}$

If the rigid body, in addition to rotating around an axis, has an additional translation movement with instantaneous velocity V then the previous formulas must be replaced by:

${displaystyle mathbf {v} ={frac {dmathbf {r} }{dt}}={boldsymbol {omega }}times mathbf {r} +mathbf {V} }$

${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={boldsymbol {alpha }}times mathbf {r} +{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r})+2{boldsymbol {omega }}times mathbf {V} +{frac {dmathbf {V} }{dt}}}$

Rotation dynamics

Angular velocity of rotation is related to angular momentum. To produce a variation in angular momentum, it is necessary to act on the system with forces that exert a moment of force. The relationship between the moment of the forces acting on the solid and the angular acceleration is known as moment of inertia (I) and represents the inertia or resistance of the solid to alter its rotational movement.

The kinetic energy of rotation is written:

${displaystyle E_{c}={frac {1}{2}}{boldsymbol {omega }}cdot (mathbf {I} {boldsymbol {omega }})}$

being ${displaystyle scriptstyle mathbf {I} }$ the tensor moment of inertia. The expression of the theorem of work in rotation movements can be expressed as follows:

${displaystyle Delta E_{c}=mathbf {M} cdot Delta {boldsymbol {theta }}}$

so that, the variation of the kinetic energy of the rigid solid is equal to the product to scale the moment of the forces by the representative vector of the rotated angle ( $Deltatheta$ ).

Axis of rotation

Although rotation is defined as a rotational movement around an axis, it should be borne in mind that said axis of rotation can change its inclination over time. This is the case with the terrestrial axis of rotation and in general with the axis of rotation of any rotating solid that does not present spherical symmetry. For a planet, or in general any rotating solid, on which a couple of force does not act, the angular momentum remains constant, although this does not imply that its axis of rotation is fixed. For a symmetrical top, that is, a solid such that two of its principal moments of inertia are equal and the third is different, the axis of rotation revolves around the direction of angular momentum. The planets with a very good approximation are flattened spheroids at the poles, which makes them a symmetrical top, for this reason their axis of rotation undergoes a rotation known as precession. The angular velocity of precession is given by the quotient between the angular moment of rotation and the smallest of the moments of inertia of the planet:

${displaystyle {dot {phi }}_{prec}={frac {L}{I_{min }}}}$

In the case of existence of axial asymmetry, the planet is an asymmetric top and also the axis of rotation can make a movement of nutation.

Rotation in mathematics

Introduction to mathematics

Detailed treatment of rotations has been the subject of numerous mathematical works, which address the problem from various points of view and degrees of sophistication: quaternions, matrices, vector operators, group theory... All these approaches are mathematically equivalent and they can be derived from each other, except in some specific aspects and possible redundant results, and the choice of one or the other depends on the specific problem. With the advent of robotics and computer graphics, the mathematics of rotations has gained new momentum and has become a very active subject of study, with particular emphasis on the quaternion-based approach.

In mathematics, rotations are linear transformations that preserve norms (that is, they are isometric) in vector spaces in which an inner product operation has been defined and whose matrix has the property of being orthogonal and of determinant equal to ±1. If the determinant is +1 it is called proper rotation and if it is −1, in addition to a proper rotation there is an inversion or reflection and we speak of improper rotation.

The conservation of the norm is equivalent to the conservation of the inner product, which can be expressed as:

${displaystyle {mathcal {R}}mathbf {a} cdot {mathcal {R}}mathbf {b} =mathbf {a} cdot mathbf {b} }$

The consequence of this is that distances and shapes are also preserved.

As a parameter that determines the rotation, you can use a vector (which has a sliding character) of the axis of rotation and of length proportional to the angle of rotation. However, the normal thing is to separate this vector into the angle and a unit vector, which in space gives four parameters. As a consequence, there are two ways to represent a single rotation, since

${displaystyle {mathcal {R}}(thetamathbf {a})={mathcal {R}}(-theta-mathbf {a})}$

Rotations in the plane

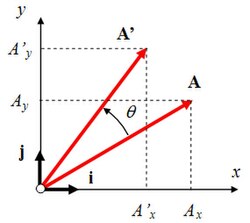
Change of base or rotation of a vector.

Let be a vector A in the Cartesian plane defined by its components x and y, described vectorially through its components:

${displaystyle mathbf {A} ={begin{bmatrix}A_{x}\A_{y}end{bmatrix}}}$

The operation of rotating the point indicated by this vector around an axis of rotation can always be written as the action of a linear operator (represented by a matrix) acting on the vector (by multiplying the vector:

${displaystyle {mathcal {R}}mathbf {A} =mathbf {A} '}$

Matrix expression

In two dimensions the rotation matrix for the given vector can be written as follows:

${displaystyle {mathcal {R}}={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}}}$

By making the operator's application, that is, by multiplying the matrix by the vector, we will get a new vector A' that has been rotated at an angle $theta$ in the anti-clockwise sense:

${displaystyle {begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}}{begin{bmatrix}A_{x}\A_{y}end{bmatrix}}={begin{bmatrix}A'_{x}\A'_{y}end{bmatrix}}}$

being

{displaystyle A'_{x}=A_{x}cos theta -A_{y}sin theta ,}

{displaystyle A'_{y}=A_{x}sin theta +A_{y}cos theta ,}

the components of the new vector after the rotation.

Expression using complex numbers

Rotations in the plane can also be handled by complex numbers, since e^iα is a rotation of angle a:

${displaystyle (x,y)in mathbb {R} ^{2}rightarrow x+iy=rho e^{iphi }in mathbb {C} {xrightarrow {mathrm {rot} }}z=e^{ialpha }(rho e^{iphi })rightarrow (mathrm {Re} (z),mathrm {Im} (z))=y(rho cos(phi +alpha),rho sin(phi +alpha))in mathbb {R} ^{2}}$ ${displaystyle (rho cos(phi +alpha),rho sin(phi +alpha))=(xcos(alpha)-ysin(alpha),xsin(alpha)+ycos(alpha))}$

The group of rotations in two dimensions is isomorphic to the Lie group, special orthogonal SO(2) which in turn is isomorphic to the unitary group U(1).

Euler's Rotation Theorem

In mathematics, Euler's rotation theorem says that any rotation or set of successive rotations can always be expressed as a rotation about a single principal direction or axis of rotation. In this way, any rotation (or set of successive rotations) in three-dimensional space can be specified through the equivalent rotation axis defined vectorially by three parameters and a fourth parameter representative of the rotated angle. These four parameters are generally called rotational degrees of freedom.

Rotations in space

The three flat rotations of the Euler angles. In the first axis is zwhich points up and rotates the axles x e andin the second axis is xwhich points to the front and bends the axis z, and in the last again the axis is z.

Three-dimensional rotations are of special practical interest because they correspond to the geometry of the physical space in which we live (naturally, provided that medium-scale regions are considered, since for large distances the geometry is not strictly Euclidean). In three dimensions, it is convenient to distinguish between flat or rectangular rotations, which are those in which the rotated vector and the one that determines the axis of rotation form a right angle, and conics, in which the angle between these vectors is not right. Planar rotations are simpler to treat mathematically, as they can be reduced to the two-dimensional case described above, while conics are much more complex and are usually treated as a combination of planar rotations (especially Euler angles and the parameters of Euler-Rodrigues).

Vector expression

The vector expression of the conical rotations is:

${displaystyle mathbf {r} '=mathbf {r} cos theta +(mathbf {u} times mathbf {r})sin theta +mathbf {u} (mathbf {u} cdot mathbf {r})(1-cos theta)}$

where:

{displaystyle mathbf {r}mathbf {r} '}

represent the vectors position of a point before and after the rotation operation.

{displaystyle mathbf {u} }

is a unitary vector that matches the direction of the spin axis.

{displaystyle theta in [0,2pi)}

is the value of the rotated angle.

{displaystyle cdottimes }

, denote respectively the climbing product and the vector product.

Matrix expressions

Matrixly, this product can be written in several ways, either as an orthogonal matrix:

${displaystyle mathbf {r} '={mathcal {R}}_{thetamathbf {u} }(mathbf {r})quad Leftrightarrow quad }$ ${displaystyle {begin{bmatrix}x'\y'\z'end{bmatrix}}={begin{bmatrix}C^{2}+S^{2}(u_{x}^{2}-u_{y}^{2}-u_{z}^{2})&2S(Su_{x}u_{y}+Cu_{z})&2S(Su_{x}u_{z}-Cu_{y})\2S(Su_{x}u_{y}-Cu_{z})&C^{2}+S^{2}(u_{y}^{2}-u_{x}^{2}-u_{z}^{2})&2S(Su_{y}u_{z}+Cu_{x})\2S(Su_{x}u_{z}+Cu_{y})&2S(Su_{y}u_{z}-Cu_{x})&C^{2}+S^{2}(u_{z}^{2}-u_{x}^{2}-u_{y}^{2})end{bmatrix}}{begin{bmatrix}x\y\zend{bmatrix}}}$

Where:

{displaystyle mathbf {r} =(x,y,z),mathbf {r} '=(x',y',z')}

{displaystyle mathbf {u} =(u_{x},u_{y},u_{z})}

{displaystyle C=cos(theta /2),S=sin(theta /2)}

It can be checked with a bit of routine algebra that the matrix above has eigenvalues:

${displaystyle {1,C+iS,C-iS}={1,e^{itheta },e^{-itheta }}}$

The main address (record generated by its own vector) associated with self-value 1 is precisely the vector ${displaystyle scriptstyle mathbf {u} }$ that gives the direction of turning axis.

Vector Expressions

Conical rotation motion can be described with vector operators that, unlike matrix expressions, are independent of coordinates. So,

${displaystyle mathbf {r} '=((1-cos theta)mathbf {uu} +cos theta +mathop {mathrm {sen} } theta {tilde {mathbf {u} }})cdot mathbf {r} }$

where the expression between parentheses works as an operator and ${displaystyle {tilde {mathbf {u} }}=mathbf {I} times mathbf {u} }$ So ${displaystyle {tilde {mathbf {u} }}cdot mathbf {r} =mathbf {u} times mathbf {r} }$ . There are certain special cases of this operator:

${displaystyle {tilde {mathbf {u} }}}$ is a flat rotation (1/2)π rad. The successive application of this operator gives ${displaystyle {tilde {mathbf {u} }}^{2}=-1}$ , ${displaystyle {tilde {mathbf {u} }}^{3}=-{tilde {mathbf {u} }}}$ , ${displaystyle {tilde {mathbf {u} }}^{4}=1}$ , ${displaystyle {tilde {mathbf {u} }}^{5}={tilde {mathbf {u} }}}$ , etc., with behavior similar to imaginary unity (i). It is a hemisimetric operator and in Castesian coordinates its matrix is:

${displaystyle {begin{pmatrix}{0}&-u_{z}&u_{y}\u_{z}&{0}&-u_{x}\-u_{y}&u_{x}&{0}\end{pmatrix}}}$

${displaystyle cos theta +sin theta {tilde {mathbf {u} }}}$ is a flat angle rotation θ. An alternative notation is ${displaystyle mathrm {e} ^{{tilde {mathbf {u} }}theta }}$ (by similarity to complex numbers). The matrix form of this operator on the main Cartesian axes is particularly simple; for example, for i is:

${displaystyle {mathcal {R}}={begin{bmatrix}1&0&0\0&cos theta &-sin theta \0&sin theta &cos theta end{bmatrix}}}$

${displaystyle 2mathbf {uu} -1}$ is a binary conical rotation (of π rad). An arbitrary conical rotation of angle θ can be represented with two binary rotations, perpendicular to ${displaystyle mathbf {u} }$ and forming an angle (1/2)θ; manipulation of this pair of binary rotations (or, equivalent, two reflections) can be taken as the basis for the description using the parameters of Euler-Rodrigues. Thus, the second of these axes is obtained by a flat rotation of the first with ${displaystyle cos {frac {1}{2}}theta +mathop {mathrm {sen} } {frac {1}{2}}theta {tilde {mathbf {u} }}}$ which gives the four parameters:

${displaystyle lambda =u_{x}mathop {mathrm {sen} } theta /2qquad mu =u_{y}sin theta /2qquad nu =u_{z}sin theta /2qquad rho =cos theta /2}$

Euler Angles

Main article: Angles of Euler

Using the Euler angles any rotation can be represented with a succession of three plane rotations around three orthogonal axes. There is no agreement on the three specific axes and various agreements appear in the scientific literature; There are, specifically, 12 possibilities, but the most common is that zyz and zxz are taken. To these 12 conventions we must add possible variations in the sign, relative orientation of the axes (clockwise or anticlockwise) and point of view (operation on vectors or transformation of coordinates).

Euler angles were the most popular system in the 19th and 20th centuries to represent rotations, since they allow easy modeling of various mechanical systems, such as spinning tops, gyroscopes, ships, and airplanes. In the case of the top, the axes correspond to precession, nutation and rotation. In airplanes they are taken as xyz axes, so that they correspond to roll (or roll in ships), pitch and yaw; this specific axis convention is also called navigation angles or Tait-Bryan angles.

Euler angles present a singularity when the angle of the second turn is 0 or π, since in such a case the first angle and the second become undefined, and only their sum is defined, if the angle is 0. This loses one degree of freedom, which in mechanical devices that combine several axes, such as gyroscopes, can lead to a system lock, known as gimbal lock (in English, gimbal lock). Mathematically, it is possible to avoid these singularities with four-parameter systems, such as Euler-Rodrigues parameters (or quaternions).

Euler-Rodrigues parameters and quaternions

Quaternions provide a method of representing singularityless rotations at the cost of being redundant. They can be introduced axiomatically or derived from vector rotations, especially using the Euler-Rodrigues construction.

Historically, the four parameters that make up the quaternions were introduced independently and with different mathematical and geometric treatments by Gauss, Rodrigues and Hamilton, among others, although apparently Euler, despite the name, was unaware of them. Rodrigues arrived at them using spherical trigonometry as a combination of reflections; Hamilton, soon after, formulated it axiomatically as an extension of the complex numbers. In quantum mechanics they were also reached with the Pauli matrices.

In three dimensions there is a construction similar to that of the complex numbers of unit module to represent the rotations in the plane. The key construction resides in identifying the three-dimensional vectors with quaternion numbers with zero real part, and using the three components as coefficients of the non-real part. The rotation can be represented as a conjugate product by a unitary quaternion obtained by exponentiation of a quaternion equal to the product of the angle rotated by the quaternion that represents the axis of rotation.

Given a three-dimensional vector $scriptstyle {mathbf {v}}$ rerepsentable as a four-tone number with a null real part, and a three-dimensional rotation given by a twist $scriptstyle alpha$ around the axis ${displaystyle scriptstyle mathbf {n} }$ can represent the resulting rotated vector as:

${displaystyle {begin{cases}mathbf {v} in mathbb {R} ^{3}mapsto v=0+v_{x}mathbf {i} +v_{y}mathbf {j} +v_{z}mathbf {k} in mathbb {H} \mathbf {v} '=R_{mathbf {n}alpha }(mathbf {v})mapsto e^{alpha (n_{x}mathbf {i} +n_{y}mathbf {j} +n_{z}mathbf {k})/2}cdot vcdot e^{-alpha (n_{x}mathbf {i} +n_{y}mathbf {j} +n_{z}mathbf {k})/2}end{cases}}}$

This approach is related to geometric algebra and the vectors i, j and k follow the algebraic rules of quaternions (i² = −1, etc.). The product of two rotations is given, in terms of ordinary vectors, by:

${displaystyle [0,mathbf {A} ][0,mathbf {B} ]=[-mathbf {A} cdot mathbf {B}mathbf {A} times mathbf {B} ]}$

where [a, b] represents a quaternion with real part a and non-real part b.

Group Theory

A full sixth round rotation (2π/6) around an axis that crosses the screen leaves the benzene molecule equal, so there is a rotational symmetry (among others).

In group theory, rotation is one of the possible transformations that can be applied to a system or a geometric figure, which allow determining the symmetry of crystallographic networks, atomic orbitals and molecules, and therefore part of their physical properties. -chemical. Other transformations are translation, reflection, and inversion.

Rotations vs. Translations

In mechanics it is shown that the movement of the rigid body can be decomposed into a rotation and a translation. Both transformations are isometric, as corresponds to the fact that the solid is rigid, but in rotation, unlike in translation, there is at least one fixed point. The set of these transformations forms a group called Euclidean group, which is the isometry group of three-dimensional Euclidean space. Each g element of this Euclidean group can be uniquely represented as:

${displaystyle gto {begin{pmatrix}R&mathbf {d} \mathbf {0} &1end{pmatrix}}in mathrm {GL} (4,mathbb {R})}$

where R is a 3x3 matrix representing rotation and d the components of the three-component vector representing displacement. Therefore this way of representing the group is a linear representation on a vector space of dimension four.

Rotations versus reflections and inversions

These three transformations are called point transformations because they leave a fixed point, and they are closely related. Thus, two reflections according to two planes are equivalent to one rotation.

The composition of two three-dimensional rotations is another rotation, so they form a group, called O(3) and which includes the reflections. The proper rotations are a subgroup, called SO(3), but the improper rotations are not, since two of them are equivalent to a proper rotation.

Perception of rotations

Outcome.

Original image of the composition.

Image shows a device to create the illusion of 3D rotation from a 2D image. It is made up of restricted parts one after the other, so that our brain interprets it as a rotation according to the data that our memory retains about the object (the head).

Contenido relacionado

Más resultados...