Rolle's theorem

In differential calculus, Rolle's theorem proves the existence of an interior point in an open interval for which the derivative of a differentiable function vanishes when the value that is at the endpoints of the interval is the same. It is generalized by the mean value theorem, of which this is a special case. It is one of the main theorems in calculus due to its applications.

It was established in 1691 by the French mathematician Michel Rolle (1652-1719).

Theorem

Yeah. f:[chuckles]a,b]→ → R{displaystyle f:[a,b]to mathbb {R} } is a continuous function at a closed interval [chuckles]a,b]{displaystyle [a,b]} differential in the open interval (a,b){displaystyle (a,b)} and f(a)=f(b){displaystyle f(a)=f(b)} then there is at least one point c한 한 (a,b){displaystyle cin (a,b)} such as

f♫(c)=0{displaystyle f'(c)=0}.

Demo

It is known that there are three possibilities, either the function we are considering is constant, or it has some point x where the value of the function is greater or this value is less than at the extremes. For the first case it is trivial that at some point the function has zero derivative (in the definition of derivative the incremental quotient is zero).

• Thanks to the continuity of f{displaystyle f} image [chuckles]a,b]{displaystyle [a,b]} is a related set of R{displaystyle mathbb {R} } and therefore it is an interval, the image interval.
• The image by a continuous function of a compact set is a compact set, and therefore the image interval is closed and finite length: it is the form [m, M], with m{displaystyle m} the minimum value f{displaystyle f} and M{displaystyle M} its maximum value.
• Yeah. m=M{displaystyle m=M}, the function is constant and any point c한 한 (a,b){displaystyle cin (a,b)} Good. Dismissed this case, mI was. I was. M{displaystyle mneq M} means one of us is not equal to f(a)=f(b){displaystyle f(a)=f(b)}. Suppose it is M{displaystyle M}. Then f(a)=f(b)}" xmlns="http://www.w3.org/1998/Math/MathML">M▪f(a)=f(b){displaystyle M vocabularyf(a)=f(b)}f(a)=f(b)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/37430052622c4c0493f8c1ec71fe67d3b5574579" style="vertical-align: -0.838ex; width:17.042ex; height:2.843ex;"/> and therefore the maximum M{displaystyle M} is reached inside the interval.
• Sea c한 한 [chuckles]a,b]{displaystyle cin [a,b]} such as f(c)=M{displaystyle f(c)=M}. By definition of the maximum, M = f(c≥ f(x) for everything x ofa, b]. Then the quotient (f(c- f(x) / (c - x) is positive when x. c (because its numerator is always positive and its denominator is positive not null), and it is negative when x ▪ c (the denominator becomes negative not null). But f'c) is by definition the limit of this quotient when x towards c. The limit on the left, f 'c^-), it has to be equal to the limit on the right, f 'c⁺). Therefore this common boundary is void, that is f♫(c)=0{displaystyle f'(c)=0}.

The demonstration is very similar if the minimum is reached in (a,b){displaystyle (a,b)}.

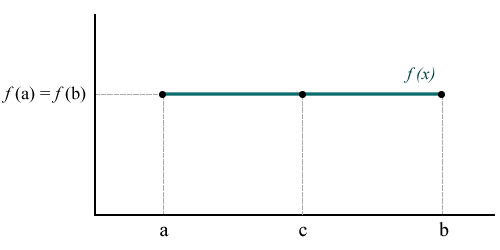
Graphically

The following chart shows the three conditions: the function is continuous at the closed interval [chuckles]a,b]{displaystyle [a,b]}It's differential in (a,b){displaystyle (a,b)} and the values that the function takes in the points a{displaystyle a} and b{displaystyle b} They're the same, I mean, f(a)=f(b){displaystyle f(a)=f(b)}. There's at least one point. c한 한 (a,b){displaystyle cin (a,b)} in which the derivative of the function is equal to zero, that is, f♫(c)=0{displaystyle f'(c)=0}. It's worth noting. c{displaystyle c} It's different from a{displaystyle a} and b{displaystyle b}. We must not confuse c with f(c), which can be equal to f(a) and f(b).

The illustration shows a constant function, but the theorem is not only true in this case. There are three cases where f(c) is different from f(a) and f(b), namely:

Case 1

The maximum point is equal a f(a){displaystyle f(a)} and f(b){displaystyle f(b)} and the minimum point is different from both, which implies that the curve is convex. The minimum point is m=f(c){displaystyle m=f(c)} and the derivative of the function at this point is 0.

Case 2

The minimum point is equal a f(a){displaystyle f(a)} and f(b){displaystyle f(b)} and the maximum point is different of both, which implies that the curve is concave. The maximum point is M=f(c){displaystyle M=f(c)} and the derivative of the function at this point is 0.

Case 3

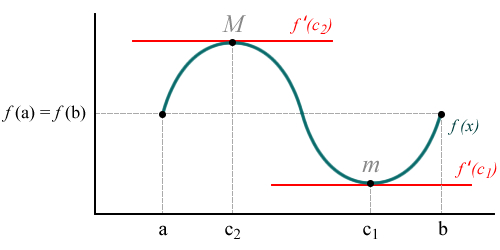
Both the minimum point and the maximum point are different a f(a){displaystyle f(a)} and f(b){displaystyle f(b)}. This means that within the closed interval [chuckles]a,b]{displaystyle [a,b]} the function reaches a maximum point M = f(c₂) greater than the value of the function at the ends a and b and a minimum m = f(c₁less than the same. Both at the maximum point and at the minimum point, the derivative of the function is null. I mean, f 'c₁= 0 and f 'c₂) = 0.

History

Indian mathematician Bhāskara II (1114–1185) is credited with knowledge of Rolle's theorem. In 1691, Michel Rolle published the first known formal proof, which does not use differential calculus. In 1834, the German Moritz Wilhelm Drobisch and the Italian Giusto Bellavitis in 1846 were the first to use the name "Rolle's theorem".