Riemann hypothesis

ImprimirCitar

Real part (red) and imaginary part (blue) of the Critical line Re(s) = 1/2 of the Riemann zeta function. You can see the first non-trivial zeros in Im(s) = ±14,135, ±21,022 and ±25,011.

A polar zeta graph, that is, Re(zeta) vs. Im(zeta), along the critical line s=it+1/2, with t values from 0 to 34.

In pure mathematics, the Riemann hypothesis, first formulated by Bernhard Riemann in 1859, is a conjecture about the distribution of the zeros of the Riemann zeta function ζ(s ).

The Riemann hypothesis, due to its relationship with the distribution of prime numbers in the set of natural numbers, is one of the most important open problems in contemporary mathematics. The Clay Institute of Mathematics has offered an award of one million dollars to the first person to develop a correct proof of the conjecture.

Definition

The Riemann zeta function ζ(s) is defined in complex numbers as the sum of an infinite series as follows:

{displaystyle zeta (s)=sum _{n=1}^{infty }{frac {1}{n^{s}}}={frac {1}{1^{s}}}+{frac {1}{2^{s}}}+{frac {1}{3^{s}}}+cdots }

y is convergent when the real part is strictly greater than 1. Leonhard Euler (who died 43 years before Riemann was born) proved that this series is equivalent to the Euler product:

{displaystyle zeta (s)=prod _{p{text{ primo}}}{frac {1}{1-p^{-s}}}={frac {1}{1-2^{-s}}}cdot {frac {1}{1-3^{-s}}}cdot {frac {1}{1-5^{-s}}}cdot {frac {1}{1-7^{-s}}}cdots {frac {1}{1-p^{-s}}}cdots }

where the infinite product extends over the set of all prime numbers p, and again converges for complexes s whose real part is greater than 1. The The convergence of the Euler product shows that ζ(s) has no zeros in this region, since none of the factors have zeros. The Riemann hypothesis deals with zeros outside the region of convergence of the sum of the series described above and the associated Euler product. To preserve the sense of this hypothesis it is necessary to analytically extend the Riemann zeta function ζ(s) in such a way that it makes sense for any value of s. In particular, it can be expressed by the following functional equation:

{displaystyle zeta (s)=2^{s}pi ^{s-1} operatorname {sen} left({frac {pi s}{2}}right) Gamma (1-s) zeta (1-s)!}

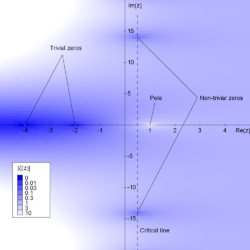
valid for all complex numbers except for s = 1, where the function has a pole. As stated above, the Riemann hypothesis deals with the zeros of this analytically extended version of the zeta function. It has certain values, called "trivial" zeros, for which the zeta function vanishes. From the equation it can be seen that s = −2, s = −4, s = −6,... (all integers negative pairs) are trivial zeros. Likewise, there are other complex values s, which satisfy the condition 0 < Re(s) < 1, for which the zeta function also vanishes, are the so-called "non-trivial" zeros. The Riemann conjecture refers to these non-trivial zeros by stating:

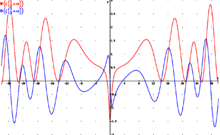
The real part of all non-trivial zero of Riemann's zeta function is 1/2

Therefore the non-trivial zeros should lie on the critical line s = 1/2 + i t, where t is a number real and i is the imaginary unit. The Riemann zeta function along the critical line has been studied in terms of the Z function, whose zeros correspond to the zeros of the zeta function on the critical line.

History

"...is ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrch "

("...it is very likely that all roots are real. Of course one would wish to have a rigorous demonstration; At the moment, after some futility attempts in vain, I have postponed your search, since it seems to be prescindible to achieve the immediate objective of my investigation.")
Riemann's statement on Riemann's hypothesis (Riemann, 1859). (Here is a version of Riemann's zeta function, modified to make its roots (zero) real instead of being on the critical line.)

Riemann mentioned the conjecture in 1859, which would be called the Riemann hypothesis, in his doctoral thesis On prime numbers less than a given magnitude, when developing an explicit formula to calculate the quantity of primes less than x. Since it was not essential to the central purpose of his article, he did not attempt to give a demonstration. He knew that the nontrivial zeros of the zeta function are distributed around the line s = 1/2 + i t, and he also knew that all nontrivial zeros must be in the range 0 ≤ Re(s) ≤ 1.

In 1896, Hadamard and de la Vallée-Poussin independently proved that no zero could lie on the line Re(s) = 1. Along with the other nontrivial properties of zeros proved by Riemann, this showed that all non-trivial zeros must lie in the interior of the critical band 0 < Re(s) < 1. This was a fundamental step for the first proofs of the prime number theorem.

In 1900, Hilbert included the Riemann hypothesis in his famous list of 23 unsolved problems — it is part of problem 8 on Hilbert's list along with Goldbach's conjecture. When asked what he would do if he woke up having slept for five hundred years, Hilbert remarkably replied that his first question would be whether the Riemann hypothesis had been proven. The Riemann hypothesis is the only problem proposed by Hilbert that is in the millennium prize from the Clay Institute of Mathematics.

In 1914, Hardy proved that there are an infinite number of zeros on the critical line Re(s) = 1/2. However it was still possible that an infinite number (and possibly most) of the non-trivial zeros would lie somewhere else on the critical band. Later work by Hardy and Littlewood in 1921 and by Selberg in 1942 gave estimates for the average density of zeros on the critical line.

Most of the mathematical community thinks the conjecture is correct, although other great mathematicians such as J. E. Littlewood and Atle Selberg have been skeptical, although Selberg's skepticism has been lessening since his younger days. In an article in 1989 he suggested that an analogue must hold true for a much broader class of functions (the Selberg class). Recent work has concentrated on explicitly calculating the location of large numbers of zeros (hoping to find some counterexample) and setting upper bounds on the proportion of zeros that can be far from the critical line (hoping to reduce them to zero).

In September 2018, Michael Atiyah, laureate of the Fields Medal (1966), among other awards, presented a proof by contradiction of the Riemann Hypothesis at the Heidelberg Laureate Forum 2018 (Germany).

The Riemann Hypothesis and Prime Numbers

The traditional formulation of the Riemann hypothesis somewhat obscures the real significance of the conjecture. The Riemann zeta function has a deep connection with prime numbers and Helge von Koch showed in 1901 that the Riemann hypothesis is equivalent to the considerable refinement of the prime number theorem: There exists a constant C > 0 such that

left|pi(x) - int_2^xfrac{dt}{ln(t)}right|le C,sqrt{x},ln(x),

for all x sufficiently large, where π(x) is the prime counter function and ln(x) is the natural logarithm of x. Lowell Schoenfeld showed that C = 1/(8 π) can be taken for all x ≥ 2657.

The zeros of the zeta function and the prime numbers satisfy certain properties of duality, known as explicit formulas, which show, using Fourier analysis, that the zeros of the Riemann zeta function can be interpreted as harmonic frequencies in the distribution of the prime numbers.

Furthermore, if the Hilbert-Polya conjecture is true, then any operator that gives us the imaginary parts of the zeros as their eigenvalues must satisfy:

sum_{n}e^{-beta E_{n}}=operatorname{tr}[e^{-beta hat H}]=e^{u/2}-e^{-u/2} frac{dpsi _{0}}{du}-frac{e^{u/2}}{e^{3u}-e^{u}},

where tr is the trace of the operator (the sum of its own values), $beta ,$ It's an imaginary number. $psi (x) ,$ It is the function of Chebyshov that adds to us the log(x) on the cousins and their entire powers, that formula is a conclusion of the 'explanatory formula' of V. Mangoldt. Several operators proposed by C. Perelman, J. Macheca and J. García seem to corroborate the results of the conjecture of Hilbert on the operator, reproducing the imaginary part of the zeros.

Numerical calculation

Absolute value of the XML function.

In 2004 Xavier Gourdon checked Riemann's conjecture numerically along the first ten trillions of non-trivial zeros of the function. However this is not strictly a demonstration, numerically it is more interesting to find a counterexample, that is to say a value of zero that does not comply with that its actual part is 1/2, as this would put the validity of the conjecture on the ground.

Until 2005, the most serious attempt to explore the zeros of the function-growth is the ZetaGrid, a computer project distributed with the ability to verify billions of zeros per day. The project ended in December 2005, and none of the zeros could be identified as a counterpart to the Riemann hypothesis.

Implications of the Riemann Hypothesis

The Riemann Hypothesis states that all other non-trivial zeros of function $zeta$ (zeta) are found in the vertical line passing through ${displaystyle {frac {1}{2}}}$ , that is, they are complex numbers of the form ${displaystyle {frac {1}{2}}+it}$ , ${displaystyle forall tin mathbb {R} }$ .

This function has a deep connection to prime numbers where the zeros of the zeta function and the prime numbers satisfy certain properties of duality, known as explicit formulas, which show, using Fourier analysis, that these zeros can be interpreted as frequencies harmonics in the distribution of prime numbers.

Knowing the relationship of the prime numbers with the function $zeta$ the implications of this function are some of these:

Precise estimators of the term of the rest of the theorem of the prime numbers:

Hege von Koch proved that the Riemann hypothesis is equivalent to the prime number theorem in which it is stated that:

There exists a constant C such that:

${displaystyle Cgeq 0:|pi (x)-Li(x)|leq C{sqrt {x}}ln x}$ ${displaystyle forall x:pi (x)=card[pgeq 2,primo,pleq x]}$ being the counting function of cousins and ${displaystyle Li(x)=int limits _{2}^{x}ln(t)dt}$

Comparison of ${displaystyle pi (x)}$ and Li(x):

For small x values had been shown ${displaystyle pi (x)leq Li(x)}$ what led to conjecture Li(x) was a strict upper upper limit ${displaystyle pi (x)}$ and therefore not the equation ${displaystyle pi (x)-Li(x)}$ has no real solutions.

However, in 1914 Littlewood used Riemann's Hypothesis to show that inequality ${displaystyle pi (x)leq Li(x)}$ is invested for sufficiently large x values.

In 1933 Skewes used Reimann's Hypothesis to show that inequality is reversed for some $<math alttext="{displaystyle xx.10101034{displaystyle x vis10^{10^{10^{34}}}}}<img alt="{displaystyle x$ and in 1955, without using the Hypothesis, showed that inequality is invested for some $<math alttext="{displaystyle xx.101010963{displaystyle x vis10^{10^{10^{96}}}}}<img alt="{displaystyle x$

Distances between consecutive prime numbers:

Cramer showed that the HR implies that there is a constant ${displaystyle C:p_{k+1}-p_{k}=C{sqrt {pk}}log p_{k}}$ where ${displaystyle p_{k}}$ It's the k-simo cousin. There is a better result than that of Cramer which is enunciated by the following conjecture:

There's always a cousin between $n^{2}$ and ${displaystyle (n+1)^{2}}$ There should be several things that imply ${displaystyle p_{k+1}-p_{k}=C{sqrt {p_{k}}}}$

However, Cramer also argued that the gap is ${displaystyle C(log p_{k})^{2}}$ .

Contenido relacionado

Más resultados...