Refractive dispersion

ImprimirCitar

Dispersion of light in two prisms of different material.

Light from a star, known as white light, is a superposition of light of different colors, each having a specific wavelength and frequency. The dispersion of light is a phenomenon that occurs when a ray of white light passes through a transparent medium (for example, air) and is refracted, showing the respective colors that constitute it at the output.

Dispersion has its origin in a decrease in the speed of propagation of light when it crosses the medium. Because the material absorbs and remits light whose frequency is close to the natural oscillation frequency of the electrons that are present in it, this light propagates a little more slowly compared to light of different frequencies. These variations in the speed of propagation depend on the refractive index of the material and oxygen; these cause light, for different frequencies, to refract differently. In the case of a double refraction (as happens in the prism) then the colors that make up the white light are distinguished in an organized way: the deviation is progressive, being greater for higher frequencies (shorter wavelengths); therefore, red light is deflected from its original path to a lesser extent than blue light.

Example

Schematic animation of a continuous beam of light scattered by a prism. The white beam represents many wavelengths of visible light, of which 7 are shown when crossing a vacuum at the same speed c. The prism makes the light slow, bending its path through the refraction process. This effect is more pronounced in shorter wavelengths (such as the violet end) than in longer wavelengths (such as the red end), thus scattering the components. When leaving the prism, each component returns to the same original speed and refracts again.

The breakdown of white light into the different colors that make it up (dating from the XVIII century) due to physical, astronomer and mathematician Isaac Newton. White light breaks down into these main colors:

Red (the color that experiences the least deviation).
Orange.
Yellow.
Green.
Blue.
Añil.
Violet (the color that experiences the greatest deviation).

This shows that white light is made up of the superposition of all these colors. Each of which experiences a different deviation since the refractive index of, for example, glass is different for each of the colors.

If light of a specific color, coming from the spectrum of white light, passed through a prism, it would not break down into other colors since each color that makes up the spectrum is a pure or monochromatic color.

Dispersion of material and waveguide

Chromatic dispersion usually refers to the dispersion of bulk material, that is, the change in refractive index with optical frequency. However, in a waveguide there is also the phenomenon of waveguide dispersion, in which case the phase velocity of a wave in a structure depends on its frequency simply due to the geometry of the waveguide. structure. More generally, waveguide dispersion can occur for waves propagating through any inhomogeneous structure (for example, a photonic crystal), regardless of whether the waves are confined. in some region.{In a waveguide, both types of scattering will generally be present, although they are not strictly additive. For example, in fiber optics the dispersion of the material and of the waveguide can effectively cancel each other out to produce a zero dispersion wavelength, important for fast fiber optic communication.

Material dispersion in optics

The variation of the refractive index vs. the vacuum wavelength for several glass. The wavelengths of visible light are highlighted in grey.

Scattering of material can be a desirable or undesirable effect in optical applications. The scattering of light by glass prisms is used to build spectrometers and spectroradiometers. However, in lenses, dispersion causes chromatic aberration, an unwanted effect that can degrade images in microscopes, telescopes, and photographic lenses.

The phase velocity, v, of a wave is a given uniform mean expressed as

{displaystyle v={frac {c}{n}}}

where c is the speed of light in a vacuum and n is the refractive index of the medium.

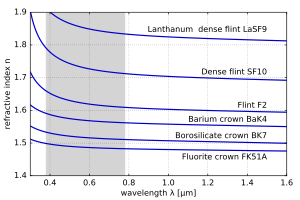
In general, the refractive index is a function of the frequency f of light, that is, n = n(f), or alternatively, with respect to the wavelength of the wave n = n(λ). The dependence of the wavelength of the refractive index of the material is usually quantified by its Abbe number or its coefficients in an empirical formula such as the Cauchy or Sellmeier equations.

Due to the Kramers-Kronig relations, the wavelength dependence of the real part of the refractive index is related to the absorption of the material, described by the imaginary component of the refractive index (also called the coefficient of extinction). In particular, for the case of non-magnetic materials (μ = μ0), the susceptibility χ that appears in the Kramers–Kronig relations is the electrical susceptibility χ_e = n² − 1.

The commonly observed consequence of dispersion in optics is the separation of white light into the color spectrum by a prism. From Snell's law it is seen that the angle of refraction of light in a prism depends on the refractive index of the material of the prism. Since this index of refraction varies with wavelength, it follows that the angle at which light is refracted will also vary with wavelength, causing an angular separation of colors known as angular dispersion.

For visible light, the refractive indices n of most transparent materials (eg, air, glass) decrease with increasing wavelength λ:

<math alttext="{displaystyle 1<n(lambda _{rm {red}})<n(lambda _{rm {yellow}})1.n(λ λ red).n(λ λ andellorw).n(λ λ blue),{displaystyle 1 habitn(lambda _{rm {red}}}) inherentn(lambda _{rm {yellow}}}}{lambda _{rm {blue}})}<img alt="{displaystyle 1<n(lambda _{rm {red}})<n(lambda _{rm {yellow}})

or alternatively:

<math alttext="{displaystyle {frac {dn}{dlambda }}dndλ λ .0.{displaystyle {frac {dn}{dlambda }}}{displaystyle}{frac {dn}{dn}{dlambda }}}}}}{displaystyle}{. !<img alt="{displaystyle {frac {dn}{dlambda }}

In this case, the medium is said to have normal dispersion. Whereas, if the index increases with the increase of the wavelength (which usually happens in the ultraviolet), the medium is said to have anomalous dispersion.

At the interface of such a material with air or a vacuum (index ~1), Snell's law predicts that light incident at an angle θ to the normal will be refracted at an angle arcsin(sin θ/n). Therefore, blue light, with a higher refractive index, will refract more strongly than red light, resulting in the well-known rainbow pattern.

Group Velocity Dispersion

Temporary evolution of a short pulse in a dispersive medium hypothetical (k=w^2) that shows that the higher wavelength components travel faster than those of lower wavelength (positive GVD), leading to a chirride and a pulse enlargement.

Beyond the simple description of a change in phase velocity with respect to wavelength, a more serious consequence of dispersion in many applications is called group velocity dispersion (GVD). Whereas the phase velocity v is defined as v = c/n , this describes only one frequency component. When combining different frequency components, such as when considering a signal or a pulse, one is usually more interested in the group velocity which describes the speed at which a pulse or information superimposed on a wave (modulation) propagates. In the accompanying animation, it can be seen that the wave itself (orange-brown) travels at a phase velocity that is much faster than the velocity of the envelope (black) which corresponds to the velocity of cluster. This pulse could be a communications signal, for example, and its information only travels at group speed even though it is made up of wave fronts moving at a higher speed (the phase speed).

It is possible to calculate the group velocity from the refractive index curve n(ω) or more directly from the wavenumber k = ωn/c where ω is the frequency in radians ω=2πf . While an expression for the phase velocity is v_p=ω/k, the group velocity can be expressed using the derivative: v _g=dω/dk. Or depending on the phase velocity v_p,

{displaystyle {v_{g}}={frac {v_{p}}{1-{frac {omega }{v_{p}}}{frac {dv_{p}}{domega }}}}.}

When there is dispersion, the group velocity is not only not equal to the phase velocity, but generally varies with the wavelength. This is known as group velocity dispersion and causes a short pulse of light to spread out as different frequency components within the pulse travel at different speeds. The group velocity spread is quantized as the derivative of the reciprocal of the group velocity with respect to the radian frequency, resulting in the group velocity spread i> = d²k/dω².

If a pulse of light propagates through a material with positive group velocity dispersion, the shorter-wavelength components travel more slowly than the longer-wavelength components. Therefore, the pulse becomes a 'positive chirp', or 'rising chirp', increasing in frequency over time. On the other hand, if a pulse travels through a material with negative group velocity dispersion, the shorter wavelength components travel faster than the longer ones, and the pulse becomes negatively chittered, or down-chirped, decreasing in frequency over time.

An everyday example of a signal with negative chirp in acoustics is an oncoming train colliding with deformations in welded track. The sound caused by the train itself is impulsive and travels much faster on metal tracks than in air, so the train can be heard long before it arrives. However, from a distance it is not heard as triggering impulses, but instead gives rise to a distinctive downward squeal, amid the reverberation caused by the complexity of the track's vibrational modes. The dispersion of the speed of the group is perceived in that the volume of the sounds remains audible for a surprisingly long time, up to several seconds.

The group velocity dispersion parameter:

{displaystyle D={frac {1}{c}},{frac {dn}{dlambda }}.}

is often used to quantify GVD, which is proportional to D via a negative factor:

{displaystyle D=-{frac {2pi c}{lambda ^{2}}},{frac {d^{2}k}{domega ^{2}}}.}

According to some authors it is said that a medium has a normal dispersion/abnormal dispersion for certain wavelengths in vacuum λ₀ if the second derivative of the refractive index calculated at λ₀ is positive/negative or, equivalently, if D(λ₀) is negative/positive. This definition refers to group velocity dispersion and should not be confused with the one given in the previous section. The two definitions do not generally coincide, so the reader must understand the context.

Generalized formulation of high dispersion orders - Lah-Laguerre Optics

Description of chromatic dispersion in a perturbative way by Taylor coefficients is advantageous for optimization problems where it is necessary to balance the dispersion of several different systems. For example, in chirp pulsed laser amplifiers, the pulses are first stretched in time by a stretcher to prevent optical damage. Later, in the amplification process, the pulses inevitably accumulate linear and non-linear phase as they pass through the materials, this blurs the radial point of the mirror, which is why it looks like this with those colors. And finally, the pulses are compressed in various types of compressors. To cancel any higher residual orders in the cumulative phase, individual orders are typically measured and balanced. However, for uniform systems, this disturbing description is usually not necessary (for example, propagation in waveguides). Scattering orders have been generalized in a computationally friendly way, in the form of Lah-Laguerre transforms.

Dispersion orders are defined by the Taylor expansion of the phase or wave vector.

${displaystyle {begin{array}{c}varphi mathrm {(} omega mathrm {)} =varphi left. right|_{omega _{0}}+left. {frac {partial varphi }{partial omega }}right|_{omega _{0}}left(omega -omega _{0}right)+{frac {1}{2}}left. {frac {partial ^{2}varphi }{partial omega ^{2}}}right|_{omega _{0}}left(omega -omega _{0}right)^{2} +ldots +{frac {1}{p!}}left. {frac {partial ^{p}varphi }{partial omega ^{p}}}right|_{omega _{0}}left(omega -omega _{0}right)^{p}+ldots end{array}}}$

${displaystyle {begin{array}{c}kmathrm {(} omega mathrm {)} =kleft. right|_{omega _{0}}+left. {frac {partial k}{partial omega }}right|_{omega _{0}}left(omega -omega _{0}right)+{frac {1}{2}}left. {frac {partial ^{2}k}{partial omega ^{2}}}right|_{omega _{0}}left(omega -omega _{0}right)^{2} +ldots +{frac {1}{p!}}left. {frac {partial ^{p}k}{partial omega ^{p}}}right|_{omega _{0}}left(omega -omega _{0}right)^{p}+ldots end{array}}}$

Dispersion relationships for the waver ${displaystyle kmathrm {(} omega mathrm {)} ={frac {omega }{c}}nmathrm {(} omega mathrm {)} }$ and phase ${displaystyle varphi mathrm {(} omega mathrm {)} ={frac {omega }{c}}{it {OP}}mathrm {(} omega mathrm {)} }$ can be expressed as:

${displaystyle {begin{array}{c}{frac {{partial }^{p}}{partial {omega }^{p}}}kmathrm {(} omega mathrm {)} ={frac {1}{c}}left(p{frac {{partial }^{p-1}}{partial {omega }^{p-1}}}nmathrm {(} omega mathrm {)} +omega {frac {{partial }^{p}}{partial {omega }^{p}}}nmathrm {(} omega mathrm {)} right) end{array}}}$ , ${displaystyle {begin{array}{c}{frac {{partial }^{p}}{partial {omega }^{p}}}varphi mathrm {(} omega mathrm {)} ={frac {1}{c}}left(p{frac {{partial }^{p-1}}{partial {omega }^{p-1}}}{it {OP}}mathrm {(} omega mathrm {)} +omega {frac {{partial }^{p}}{partial {omega }^{p}}}{it {OP}}mathrm {(} omega mathrm {)} right)end{array}}(1)}$

Deriving from any differential function ${displaystyle fmathrm {(} omega mathrm {|} lambda mathrm {)} }$ in wavelength or frequency space is specified through a transformation of Lah as:

${displaystyle {begin{array}{l}{frac {partial {p}}{partial {omega }^{p}}}fmathrm {(} omega mathrm {)} ={}{left(mathrm {-} mathrm {1} right)}^{p}{left({frac {lambda }{mathrm {2} pi c}}right)}^{p}sum limits _{m={0}}^{p}{{mathcal {A}}mathrm {(} p,mmathrm {)} {lambda }^{m}{frac {{partial }^{m}}{partial {lambda }^{m}}}fmathrm {(} lambda mathrm {)} }end{array}}}$ ${displaystyle}$ ${displaystyle {begin{array}{c}{frac {{partial }^{p}}{partial {lambda }^{p}}}fmathrm {(} lambda mathrm {)} ={}{left(mathrm {-} mathrm {1} right)}^{p}{left({frac {omega }{mathrm {2} pi c}}right)}^{p}sum limits _{m={0}}^{p}{{mathcal {A}}mathrm {(} p,mmathrm {)} {omega }^{m}{frac {{partial }^{m}}{partial {omega }^{m}}}fmathrm {(} omega mathrm {)} }end{array}}(2)}$

The elements of the transformation matrix are Lah coefficients: ${displaystyle {mathcal {A}}mathrm {(} p,mmathrm {)} ={frac {pmathrm {!} }{left(pmathrm {-} mright)mathrm {!} mmathrm {!} }}{frac {mathrm {(} pmathrm {-} mathrm {1)!} }{mathrm {(} mmathrm {-} mathrm {1)!} }}}$

Written for GDD the previous expression states that a constant with GGD wavelength will have zero higher orders. The higher orders evaluated from GDD are: ${displaystyle {begin{array}{c}{frac {{partial }^{p}}{partial {omega }^{p}}}GDDmathrm {(} omega mathrm {)} ={}{left(mathrm {-} mathrm {1} right)}^{p}{left({frac {lambda }{mathrm {2} pi c}}right)}^{p}sum limits _{m={0}}^{p}{{mathcal {A}}mathrm {(} p,mmathrm {)} {lambda }^{m}{frac {{partial }^{m}}{partial {lambda }^{m}}}GDDmathrm {(} lambda mathrm {)} }end{array}}}$

Replace the equation (2) expressed for the refractive index $n$ or optical path ${displaystyle OP}$ in the equation (1) expressions are obtained in a closed way for dispersion orders. Generally dispersion of order ${displaystyle p^{th}}$ POD is a Laguerre-type transformation of negative order two:

${displaystyle POD={frac {d^{m}varphi (omega)}{domega ^{m}}}=(-1)^{p}({frac {lambda }{2pi c}})^{(p-1)}sum _{m=0}^{p}{mathcal {B(p,m)}}(lambda)^{m}{frac {d^{m}OP(lambda)}{dlambda ^{m}}}}$ ${displaystyle}$ ${displaystyle POD={frac {d^{m}k(omega)}{domega ^{m}}}=(-1)^{p}({frac {lambda }{2pi c}})^{(p-1)}sum _{m=0}^{p}{mathcal {B(p,m)}}(lambda)^{m}{frac {d^{m}n(lambda)}{dlambda ^{m}}}}$

The elements of the matrix of the transformations are the coefficients of Laguerre without a sign of order minus 2, and are given as: ${displaystyle {mathcal {B}}mathrm {(} p,mmathrm {)} ={frac {pmathrm {!} }{left(pmathrm {-} mright)mathrm {!} mmathrm {!} }}{frac {mathrm {(} pmathrm {-} mathrm {2)!} }{mathrm {(} mmathrm {-} mathrm {2)!} }}}$

The first ten scattering orders, written explicitly for the wave vector, are:

${displaystyle {begin{array}{l}{boldsymbol {it {GD}}}={frac {partial }{partial omega }}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(nmathrm {(} omega mathrm {)} +omega {frac {partial nmathrm {(} omega mathrm {)} }{partial omega }}right)={frac {mathrm {1} }{c}}left(nmathrm {(} lambda mathrm {)} -lambda {frac {partial nmathrm {(} lambda mathrm {)} }{partial lambda }}right)=v_{gr}^{mathrm {-} mathrm {1} }end{array}}}$

The Group Refraction Index ${displaystyle n_{g}}$ is defined as: ${displaystyle n_{g}=cv_{gr}^{mathrm {-} mathrm {1} }}$ .

${displaystyle {begin{array}{l}{boldsymbol {it {GDD}}}={frac {{partial }^{2}}{partial {omega }^{mathrm {2} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {2} {frac {partial nmathrm {(} omega mathrm {)} }{partial omega }}+omega {frac {{partial }^{2}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {2} }}}right)={frac {mathrm {1} }{c}}left({frac {lambda }{mathrm {2} pi c}}right)left({lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}right)end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {TOD}}}={frac {{partial }^{3}}{partial {omega }^{mathrm {3} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {3} {frac {{partial }^{2}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {2} }}}+omega {frac {{partial }^{3}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {3} }}}right)={-}{frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {2} }{Bigl (}mathrm {3} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+{lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {FOD}}}={frac {{partial }^{4}}{partial {omega }^{mathrm {4} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {4} {frac {{partial }^{3}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {3} }}}+omega {frac {{partial }^{4}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {4} }}}right)={frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {3} }{Bigl (}mathrm {12} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {8} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+{lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {FiOD}}}={frac {{partial }^{5}}{partial {omega }^{mathrm {5} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {5} {frac {{partial }^{4}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {4} }}}+omega {frac {{partial }^{5}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {5} }}}right)={-}{frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {4} }{Bigl (}mathrm {60} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {60} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {15} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+{lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {SiOD}}}={frac {{partial }^{6}}{partial {omega }^{mathrm {6} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {6} {frac {{partial }^{5}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {5} }}}+omega {frac {{partial }^{6}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {6} }}}right)={frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {5} }{Bigl (}mathrm {360} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {480} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {180} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {24} {lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+{lambda }^{mathrm {6} }{frac {{partial }^{6}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {SeOD}}}={frac {{partial }^{7}}{partial {omega }^{mathrm {7} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {7} {frac {{partial }^{6}nmathrm {(} omega mathrm {)} }{{partial omega }^{mathrm {6} }}}+omega {frac {{partial }^{7}nmathrm {(} omega mathrm {)} }{{partial omega }^{mathrm {7} }}}right)={-}{frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {6} }{Bigl (}mathrm {2520} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {4200} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {2100} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {420} {lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {35} {lambda }^{mathrm {6} }{frac {{partial }^{6}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+{lambda }^{mathrm {7} }{frac {{partial }^{7}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {EOD}}}={frac {{partial }^{8}}{partial {omega }^{mathrm {8} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {8} {frac {{partial }^{7}nmathrm {(} omega mathrm {)} }{{partial omega }^{mathrm {7} }}}+omega {frac {{partial }^{8}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {8} }}}right)={frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {7} }{Bigl (}mathrm {20160} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {40320} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {25200} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {6720} {lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {840} {lambda }^{mathrm {6} }{frac {{partial }^{6}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+\+mathrm {48} {lambda }^{mathrm {7} }{frac {{partial }^{7}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+{lambda }^{mathrm {8} }{frac {{partial }^{8}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {NOD}}}={frac {{partial }^{9}}{partial {omega }^{mathrm {9} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {9} {frac {{partial }^{8}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {8} }}}+omega {frac {{partial }^{9}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {9} }}}right)={-}{frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {8} }{Bigl (}mathrm {181440} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {423360} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {317520} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {105840} {lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {17640} {lambda }^{mathrm {6} }{frac {{partial }^{6}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+\+mathrm {1512} {lambda }^{mathrm {7} }{frac {{partial }^{7}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+mathrm {63} {lambda }^{mathrm {8} }{frac {{partial }^{8}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}+{lambda }^{mathrm {9} }{frac {{partial }^{9}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {9} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{boldsymbol {it {TeOD}}}={frac {{partial }^{10}}{partial {omega }^{mathrm {10} }}}kmathrm {(} omega mathrm {)} ={frac {mathrm {1} }{c}}left(mathrm {10} {frac {{partial }^{9}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {9} }}}+omega {frac {{partial }^{10}nmathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {10} }}}right)={frac {mathrm {1} }{c}}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {9} }{Bigl (}mathrm {1814400} {lambda }^{mathrm {2} }{frac {{partial }^{2}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {4838400} {lambda }^{mathrm {3} }{frac {{partial }^{3}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {4233600} {lambda }^{mathrm {4} }{frac {{partial }^{4}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+{1693440}{lambda }^{mathrm {5} }{frac {{partial }^{5}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+\+mathrm {352800} {lambda }^{mathrm {6} }{frac {{partial }^{6}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+mathrm {40320} {lambda }^{mathrm {7} }{frac {{partial }^{7}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+mathrm {2520} {lambda }^{mathrm {8} }{frac {{partial }^{8}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}+mathrm {80} {lambda }^{mathrm {9} }{frac {{partial }^{9}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {9} }}}+{lambda }^{mathrm {10} }{frac {{partial }^{10}nmathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {10} }}}{Bigr)}end{array}}}$

Explicitly, written for the phase $varphi$ , the first ten dispersion orders can be expressed depending on the wavelength using the transformations of Lah (equation (2)) as:

${displaystyle {begin{array}{l}{frac {partial varphi mathrm {(} omega mathrm {)} }{partial omega }}={-}left({frac {mathrm {2} pi c}{{omega }^{mathrm {2} }}}right){frac {partial varphi mathrm {(} omega mathrm {)} }{partial lambda }}={-}left({frac {{lambda }^{mathrm {2} }}{mathrm {2} pi c}}right){frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{2}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {2} }}}={frac {partial }{partial omega }}left({frac {partial varphi mathrm {(} omega mathrm {)} }{partial omega }}right)={left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {2} }left(mathrm {2} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+{lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}right)end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{3}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {3} }}}={-}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {3} }left(mathrm {6} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {6} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+{lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}right)end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{4}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {4} }}}={left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {4} }{Bigl (}mathrm {24} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {36} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {12} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+{lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{mathrm {5} }varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {5} }}}={-}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {5} }{Bigl (}mathrm {120} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {240} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {120} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {20} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+{lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{6}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {6} }}}={left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {6} }{Bigl (}mathrm {720} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {1800} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {1200} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {300} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {30} {lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}mathrm { +} {lambda }^{mathrm {6} }{frac {{partial }^{6}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{7}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {7} }}}={-}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {7} }{Bigl (}mathrm {5040} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {15120} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {12600} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {4200} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {630} {lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {42} {lambda }^{mathrm {6} }{frac {{partial }^{6}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+{lambda }^{mathrm {7} }{frac {{partial }^{7}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{8}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {8} }}}={left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {8} }{Bigl (}mathrm {40320} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {141120} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {141120} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {58800} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {11760} {lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {1176} {lambda }^{mathrm {6} }{frac {{partial }^{6}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+mathrm {56} {lambda }^{mathrm {7} }{frac {{partial }^{7}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+\+{lambda }^{mathrm {8} }{frac {partial ^{8}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}{Bigr)}end{array}}}$ ${displaystyle {begin{array}{l}{frac {{partial }^{9}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {9} }}}={-}{left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {9} }{Bigl (}mathrm {362880} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {1451520} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {1693440} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {846720} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {211680} {lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {28224} {lambda }^{mathrm {6} }{frac {{partial }^{6}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+\+mathrm {2016} {lambda }^{mathrm {7} }{frac {{partial }^{7}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+mathrm {72} {lambda }^{mathrm {8} }{frac {{partial }^{8}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}+{lambda }^{mathrm {9} }{frac {partial ^{mathrm {9} }varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {9} }}}{Bigr)}end{array}}}$

${displaystyle {begin{array}{l}{frac {{partial }^{10}varphi mathrm {(} omega mathrm {)} }{partial {omega }^{mathrm {10} }}}={left({frac {lambda }{mathrm {2} pi c}}right)}^{mathrm {10} }{Bigl (}mathrm {3628800} lambda {frac {partial varphi mathrm {(} lambda mathrm {)} }{partial lambda }}+mathrm {16329600} {lambda }^{mathrm {2} }{frac {{partial }^{2}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {2} }}}+mathrm {21772800} {lambda }^{mathrm {3} }{frac {{partial }^{3}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {3} }}}+mathrm {12700800} {lambda }^{mathrm {4} }{frac {{partial }^{4}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {4} }}}+mathrm {3810240} {lambda }^{mathrm {5} }{frac {{partial }^{5}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {5} }}}+mathrm {635040} {lambda }^{mathrm {6} }{frac {{partial }^{6}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {6} }}}+\+mathrm {60480} {lambda }^{mathrm {7} }{frac {{partial }^{7}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {7} }}}+mathrm {3240} {lambda }^{mathrm {8} }{frac {{partial }^{8}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {8} }}}+mathrm {90} {lambda }^{mathrm {9} }{frac {{partial }^{9}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {9} }}}+{lambda }^{mathrm {10} }{frac {{partial }^{10}varphi mathrm {(} lambda mathrm {)} }{partial {lambda }^{mathrm {10} }}}{Bigr)}end{array}}}$

Contenido relacionado

Más resultados...