Redemption interaction
The magnetic exchange interaction is an effect described by quantum mechanics that occurs between unpaired electrons of the same or different atoms or ions, when their wave functions overlap, that is, when they are relatively close. In a simplified way, the energy of two electrons, when they are very close, depends on the symmetry of their orbitals, that is, on their distribution in space, and therefore on the relative orientation of their spins, their intrinsic angular momenta. This interaction is a manifestation of the Pauli exclusion principle, which has a notable effect on chemistry and therefore on everyday life, since it is related to the short-range repulsion between atoms or molecules, and which prevents matter from collapsing. It is also of fundamental importance in magnetism, since by altering the energy of states depending on the arrangement of electronic spins, it is one of the main processes by which magnetic moments align with each other. In this way, it is at the base of a good part of the magnetic phenomena, both those of academic interest and those of industrial and social importance.
The phenomenon and its main effects were already described within the framework of quantum mechanics in 1926, but in the following decades different models followed one another to describe similar or related phenomena, or the same phenomenon in particular contexts. In magnetism, the terms exchange and magnetic exchange are used interchangeably in different contexts and with different meanings related to this interaction. The effective Hamiltonian parameter that describes the exchange interaction, and which is proportional to the difference in energy between states with different magnetic moment, is called exchange, for example. It is sometimes used in contrast to superexchange, to indicate that the interaction takes place by direct overlap between the magnetic orbitals, and is not mediated by a diamagnetic bridge. With more or less property, derived terms are used in different physical models that also describe the energetic separation of states of different magnetic moment.
This article gives a historical introduction to some of the main concepts related to magnetic swapping. First, a quantitative definition of the variable most directly related to this interaction is given: the so-called integral or exchange energy. Starting from this base, the main theoretical tools are presented to describe the magnetic exchange in its simplest form: the Ising and Heisenberg Hamiltonians, and the XY model. Below are some models for processes related to the exchange, more sophisticated or complex, and generally also more far-reaching. Finally, the Hubbard model and the density functional theory are mentioned, and their relationship with the exchange interaction is exposed.
Integral or exchange energy
The effects of the exchange interaction were discovered independently by the physicists Werner Heisenberg and Paul Dirac in 1926; the exchange interaction is also closely related to that of Pauli's principle of exclusion, set out in 1925. It arises naturally when considering the indistinguishability of some particles in quantum mechanics: while in classical mechanics the particles are distinguishable and described with the statistics of Maxwell-Boltzmann, in the context of quantum mechanics there is no physical procedure to distinguish them or to say if a particle observed in an instant is the same as another observed in a later moment. This circumstance makes the proper quantum treatment of the identical particles require Bose-Einstein statistics, if the identical particles are boson or Fermi-Dirac, if they are fermions. In this context, the ♪ or exchange between two electrons with positions r→ → 1,r→ → 2{displaystyle {vec {r}_{1},{vec {r}}}_{2}}} and spins s1,s2 or, in general, between two feminine, carries a change of sign of the wave function: that defines mathematically the system:
END END (r→ → 2,s2;r→ → 1,s1)=− − END END (r→ → 1,s1;r→ → 2,s2){displaystyle psi ({vec {r}_{2},s_{2};{vec {r}}},s_{1})=-psi ({vec {r}},s_{1},s_{1};{vec {r}}},s_{2})
In this respect, fermions contrast with bosons, for which the exchange between two particles maintains the identical wave function. Note that all observable properties depend on the square of the wave function. The exchange of two identical particles, be they bosons or fermions, does not change the absolute value of the wave function, and therefore does not change any physical property.
The basic difference between bosons and fermions is that the former can be grouped in the same state and position in any number of them, as occurs with photons in a laser. On the other hand, identical fermions cannot be in the same position and in the same state. The three electrons of a lithium atom in its lowest energy state cannot be in the 1s orbital and with spin up, despite the fact that this is the most stable orbital: it will have two 1s electrons, one with spin up and one with spin down, and one 2s electron.
The exchange interaction has no classical analogue, and it alters the expected value of the energy of the states according to their spatial symmetry, which translates into different spin symmetry and different expected value of the magnetic moment. The exchange energy denoted J12, which is produced by the Coulomb repulsion between two electrons 1 and 2, which can be described by the wave functions ϕA and ϕB, and having the same spin quantum number is given, in Dirac's bra-ket notation:
J12 = φ φ A(1)φ φ B(2)日本語e2r12日本語φ φ A(2)φ φ B(1) {displaystyle langle J_{12}rangle =leftlangle phi _{A^}{B}phi _{B}{(2)}left ultimate{frac {e^{2}}}{r_{12}}}}}{Right?
, where e is the elementary charge and r12 is the expected value of the distance between the electrons. It is sometimes called the trade integral because it can also be expressed as an integral over the entire type space:
- J12=∫ ∫ φ φ A↓ ↓ (r1)φ φ B↓ ↓ (r2)VI(r1,r2)φ φ B(r1)φ φ A(r2)dr1dr2.{displaystyle J_{12}=int phi _{A}^{*}(r_{1})phi _{B^{*}(r_{2})V_{I}(r_{1},r_{2})phi _{B}(r_{1})phi _{A}(r_{2}{1},{2}{1}{1}{. !
Where {r1,r2!{displaystyle scriptstyle {r_{1},,r_{2}}}} represent the three spatial coordinates of each electron {x1,and1,z1,x2,and2,z2!{displaystyle scriptstyle {x_{1},,y_{1},,z_{1},,x_{2},,y_{2},,z_{2}{2}}}}}φ♪ is the complex conjugated function of φ and the interaction VI(r1,r2){displaystyle scriptstyle V_{I}(r_{1},r_{2}}}}} may have the shape e2/r12{displaystyle scriptstyle e^{2}/r_{12}}. This integral stabilizes the triplet of thorn, according to Hund's rule.
This interaction is part of electronic correlation, and is related to what is known as a Fermi hole: the tendency of an electron with a quantum number of spin not to be located at the same point in space as another electron with the same number of spin. same spin quantum number; as opposed to two bosons, which tend to be closer together than they would be if they were distinguishable particles. If you calculate the expected value of the distance between two particles in a symmetric or antisymmetric state, you can see the effect of the interaction of exchange. Thus, this interaction is responsible for the repulsive addend in the Lennard-Jones potential, or, in chemical terms, the steric effect: causing two atoms to "bump" into each other instead of interpenetrating i> freely. Dyson and Lenard showed that, without the participation of this effect, the attraction between nuclei and electrons would prevail over the nucleus-nucleus and electron-electron repulsions, resulting in the collapse of matter.
It should be emphasized that this interaction is not magnetic in nature, but electrical. However, as developed in the rest of this article, some of its most notable effects are magnetic, and it is for this reason that it is called called, somewhat inappropriately, magnetic exchange. Moreover, as explained below, it is called by analogy "dipole exchange" or "exchange through space" to what is nothing more than a dipole magnetic interaction.
Direct Exchange Hamiltonians
In quantum mechanics, each observable physical property corresponds mathematically to a self-adjoint operator defined on the Hilbert space that is used to represent the physical states of the system. In the case of energy, that operator is the Hamiltonian. When the internal dynamics of a process are not well known, or when they are too complex to deal with explicitly, it is very common to use approximate model Hamiltonians, which are based on fictitious and simplified mechanics to reproduce the values of interest. In this context, there are three clearly differentiated model Hamiltonians to rationalize direct trade effects, which are more or less appropriate for different types of systems and are presented below in the historical order in which they were proposed.
Ising Hamiltonian
The Ising Hamiltonian was born as a mathematical model to explain ferromagnetism from statistical mechanics. It was posed as a problem by Wilhelm Lenz to his student Ernst Ising, who solved it in 1925 for the case of one dimension; in this specific case, no transition to the ferromagnetic phase from the paramagnetic phase is found. solved a year before the discovery of the exchange interaction as a quantum mechanical effect.
The Ising Hamiltonian is based on the reduction of the possible values of the spin to two unique projections sz on the z-axis of values {+1,-1 }:
siz=± ± 1{displaystyle s_{i}{z}=pm 1}
and therefore the energy of the system is defined by the Zeeman effect of the external magnetic field Hz on those projections sz , plus an Jij interaction between them. Due to its origin as a statistical mechanics model, it is generally posed for a set of spins:
H^ ^ =− − ␡ ␡ ijJijsizsjz− − Hz␡ ␡ i=1Nsiz{displaystyle {hat {H}}=-sum _{ij}J_{ij}s_{i}{i}{z}s_{j}{z}-H_{z}sum _{i=1}{n}s_{i}{i}{z}}
In practical terms, it makes sense to consider it, for example, when the zero-field splitting of the system is such that, below a certain temperature, the interaction occurs only between the projections on the z-axis of the spin; in other words, if the spin resides primarily on one axis, it is usually worth simplifying the calculations by considering only that axis.
The following dynamic animations show the results of the Ising model in two dimensions for different relationships between magnetic exchange and temperature, so that depending on whether or not temperatures are below the critical point, formation is reached or not of magnetic domains. It is seen how at temperatures below the critical point the system is ordered in well-differentiated magnetic domains, which are represented in the diagrams by areas of different colors. At the critical point between ferromagnetism and paramagnetism, you begin to see this appearance of domains, but they do not consolidate.
Heisenberg Hamiltonian
The Hamiltonian Heisenberg or Heisenberg-Dirac-van-Vleck is a hamiltonian model (fenomenological) of magnetic exchange, proposed in 1928 by Werner Heisenberg and Paul Dirac. It can be seen as a generalization of the Ising model, where the spin or the interaction between spins does not have to be limited to an axis, and the operator is used of the total magnitude of the spin S^ ^ {displaystyle {hat {s}}}. As for the sign or prefactor, there is no unity between physicists and different magnetochemical schools, but in any case the magnitude of the exchange J it is proportional to the difference of energy between the states of different thorn and its sign corresponds to the ferrommetic or antiferromagnetic character of the interaction.
H^ ^ =JS^ ^ 1S^ ^ 2 H^ ^ =− − JS^ ^ 1S^ ^ 2 H^ ^ =− − 2JS^ ^ 1S^ ^ 2{displaystyle {hat {H}}=J{hat {S}{hat {s}{hat {s}}_{2}}{2quad vee quad {hat {H}}}{-J{hat}{s}{1}{s}{hat {s}}{2}{quad vee quad {quad {hat {b}{b}}}}}{b {b {b {cH}}}}}}}{bright}}{bright}}{cH}}{cH}}{cH}}{cH}{cH}}{cH}}}{cH}{bright}}}}{cH}}{cH}{bright}{bright}}{bright}{cH}{bright}}{cH}{bright}}{cH}}{cH}}{
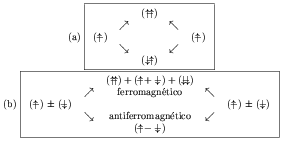
A simplified representation is shown in figure (a), in which we see that, starting from two states, each corresponding to an electron on a magnetic center, we arrive at two states, one of them with moments magnetic fields of paired electrons ferromagnetically (parallel) and one antiferromagnetically (antiparallel).
Figure (b) gives a slightly more detailed picture, emphasizing the fermionic nature of electrons, and expressing the states as Slater determinants. Thus, it is seen that the ferromagnetic state is a triplet, and the antiferromagnetic state is a singlet. The exchange between two identical fermions is accompanied by a change in the sign of the wave function, thus the triplet, which is spin symmetric, is spatially antisymmetric, and the singlet, which is spin antisymmetric, is space symmetric.
The magnetic exchange interaction between two unpaired electrons is fundamentally due to the Coulomb repulsion between their electrical charges, operating under the laws of quantum mechanics. The contribution of the "direct", "dipole" or "through space" magnetic interaction is comparatively very weak, and can be almost generally neglected (although in the cases of interactions between a large number of spins, such as the In the case of ferromagnetic planes, with a very large magnetic moment, the interaction "through space" becomes important.
XY-Model
In the 1960s, the XY model was studied, as a particular case of the Heisenberg model, complementary to the Ising model, in the sense that the Ising Hamiltonian can be derived from the Heisenberg model with Jx = Jy = 0 while the XY model is the one obtained if Jz = 0. It can be thought that if the Ising model describes spins with an easily magnetized axis, the XY model describes spins with an easily magnetized plane. These three models have been called particular cases of an N-dimensional model, where N refers to the dimension of each spin, not to that of the lattice that contains them.
Beyond direct exchange
It is possible to find phenomena with effects analogous to the exchange interaction as described, or that combine the exchange interaction with other processes such as electronic transfer. The so-called super swap, for example, takes place through an intermediary, with no direct overlap between the orbitals in which the magnetic moment resides. The double exchange has an effect comparable to the exchange, it also takes place through an intermediary and only occurs in mixed valence systems, since it is mediated by delocalized electrons between the two magnetic orbitals. The indirect exchange goes a step further in the same sense, and consists of the indirect communication between two magnetic moments through an intermediate electrical conductive system. Finally, dipole interaction is a totally different phenomenon, purely magnetic, although it has effects similar to those resulting from spin-orbit interaction combined with other types of exchange, known as anisotropic exchange. For systems with a certain symmetry, the anisotropic exchange has to be completed by a term called antisymmetric.
Super Swap and Biquadratic Swap
The name super exchange (or Kramers-Anderson super exchange ) is given to the magnetic coupling that occurs between two atoms or ions whose magnetic orbitals do not directly overlap, but rather takes place through a diamagnetic bridge, such as in the simplest cases an oxo anion (O2-), a halogen (F-, Cl-,...) or a simple atom or ion, such as carbon monoxide or cyanide. It was first proposed by Hendrik Kramers in 1934 when he noted that in crystals such as manganese(II) oxide MnO, the Mn2+ ions interacted magnetically despite being separated by an oxygen anion, nonmagnetic. Phillip Anderson refined the model in 1950. Goodenough and Loeb, in 1955, emphasized the fundamentally covalent character of this interaction. This rationalizes the fact that in the chalcogen series (MnO, MnS, MnSe) increases the Néel temperature: the p orbitals of the heavier chalcogens are wider and better overlap with the Mn orbitals.
It can be understood as the result of a spin polarization of the bridge electrons, generally doubly occupied p orbitals, by partially occupied magnetic orbitals, generally d or f type. The interaction is more or less strong depending on the size of the bridge and the amount of overlap between the magnetic orbitals and the bridge orbitals. By the Pauli exclusion principle, the total spin of the doubly occupied orbital will be zero, so if one lobe is spin up polarized, the opposite lobe will be spin down polarized. /i>.
The resulting coupling sign is ferromagnetic or antiferromagnetic depending on the character of the overlap and the orbitals involved. In simple cases, such as two cations of the same element in the same oxidation state, the character of the super exchange can be predicted by the cation-bridge-cation angle: 180 degree angles imply antiferromagnetic coupling and 90 degree angles ferromagnetic coupling, with a sign change to an intermediate angle that depends on the system. Relevant examples are oxides with a sodium chloride type structure, in which the super exchange has an antiferromagnetic character. In spinels it also has an antiferromagnetic character but results in a ferrimagnetic global ordering.
In 1963, in order to quantitatively rationalize the behavior of Mn(II) ion pairs inserted in a MgO lattice, which has somewhat shorter bond distances, Owen and Harris introduced the biquadratic exchange (in contrast to the bilinear swapping of the Heisenberg Hamiltonian), citing previous work by Anderson to justify its occurrence in systems with super swapping. This biquadratic swapping j, as a correction to the bilinear hamiltonionian, has the form
H^ ^ =J⋅ ⋅ S^ ^ 1S^ ^ 2+j⋅ ⋅ (S^ ^ 1S^ ^ 2)2{displaystyle {hat {H}}=Jcdot {hat {S}}_{1{hat {S}_{2}_{2}+jcdot left({hat {S}}}}_{1}{hat {S}_{2}{2}{2}{2}}}{2}}}{2}}}}
and Owen and Harris indicated that values of j one or two orders of magnitude less than J are consistent with Anderson's super-exchange theory. A mechanism that can produce a similar effect is due to magnetoelastic energy, related to magnetostriction: if bond distances are altered by exchange energy, changes in exchange result in an interaction amplified; this phenomenon becomes especially relevant when the temperature varies.
Double redemption
A double exchange is known as a physical model of exchange, proposed by Clarence Zener in 1951, and related to electronic transfer. It starts from two magnetic atoms connected by a third, and that one of the two magnetic atoms has an extra electron compared to the other. The model consists of the sharing of two electrons between the three atoms, with the particularity that the electrons do not change spin during the swap. By Hund's rule, this makes the process more or less likely depending on the respective alignment of the spins on the source atom and the destination atom. As the delocalization of the electron helps to reduce the kinetic energy and therefore stabilizes the system, a ferro- or antiferromanetic exchange is favored depending on the filling of the magnetic orbitals, as predicted by the Goodenough-Kanamori rules.
The resemblance to the super-exchange process is only apparent: the double-exchange process in a system that is not of mixed valence, such as Mn+2 O-2 Mn+2 discussed above would be heavily disadvantaged, since the result would be an unstable state:
- Mn2+ O-2 Mn+2 {displaystyle quad quad nrightarrow quad quad } Mn+ O-2 Mn+3
In contrast, in mixed valence systems, the result of the process has the same energy as the original state, so it can be seen as a resonance process, that is, a mixture of states:
- Mn2+ O-2 Mn+3 ▪ ▪ {displaystyle quad quad leftrightarrow quad quad } Mn3+ O-2 Mn+2
Indirect redemption or RKKY interaction
The indirect exchangeAlso called interaction RKKY o Ruderman-Kittel-Kasuya-Yosida is a mechanism of angular moment coupling between fixed magnetic moments through delocalized electrons. Ruderman and Kittel proposed in 1954 the basis of this mechanism to explain the width of nuclear magnetic resonance lines in metallic silver. They used the theory of second order disturbances to propagate hyperphine interaction Δkmkm of nuclear spins I→ → {displaystyle {vec {I}}} with wave vector conduction electrons km and effective mass m* and establish an indirect exchange between cores separated by each other for a distance Rijthrough the following Hamiltonian:
H(Rij)=I→ → i⋅ ⋅ I→ → j4日本語Δ Δ kmkm日本語2m↓ ↓ (2π π )3Rij4 2[chuckles]2kmRij# (2kmRij)− − without (2kmRij)]{displaystyle H(mathbf {R} _{ij})={frac {{vec {I}}}}{i}{i}{idot {vec {I}{I}}{j}}}{4}{frac}{left
where, of course, {displaystyle hbar } is the constant of Planck divided by 2 π.
In 1955 and 1956 respectively, Tadao Kasuya proposed extending the theory to include indirect coupling between inner d electrons, and Kei Yosida formulated the general theory for both nuclei and electrons.
Anisotropic exchange and dipole interaction
The swap interaction as it was presented in the 1920s, including the upper nuances, is fundamentally isotropic: by its nature, it cannot depend on the spatial orientation of the spins. The spatial rotation of a molecule in a magnetic field of fixed direction would have no appreciable consequence on the magnetic properties that can be deduced from this interaction. Often this is not exact, and occasionally it is not even an acceptable approximation. In the 1950s it was shown for the first time that this is mainly due to dipole magnetic interaction, and the so-called anisotropic exchange.
The dipolar interaction between quantum magnetic moments is analogous to that between classic magnetic moments, or magnets. Magnetic flow B→ → {displaystyle {vec {B}}} generated by a dipolar moment m→ → {displaystyle {vec {m}}} position r→ → {displaystyle {vec {r}}} is in both cases:
B→ → (r→ → )=μ μ 04π π 3r→ → (m→ → ⋅ ⋅ r→ → )− − m→ → r2r5{displaystyle {vec {B}}({vec {r}}}),=,{frac {mu _{0}}{4pi }}}{frac {3{vec {r}}}{vec {m}}}{cdot {vec {r}}{vec {m}{r^{5}}}{5}}}}}{
Where μ μ 0{displaystyle mu _{0}} is the magnetic permeability of the vacuum. Obviously, the sign and magnitude of this interaction depends on the angle between the vector r→ → {displaystyle {vec {r}}} connecting to magnetic centers and guidance m1→ → {displaystyle {vec {m_{1}}}}},m2→ → {displaystyle {vec {m_{2}}}}} of them. As in the case of two bar magnets, the interaction will be of maximum intensity if the magnets are oriented in parallel to the line that unites them, will be annulled for a certain angle (approx. 54.74°) and will present another local maximum when the magnets are perpendicularly oriented to the line that unites them.
This interaction, although always present, is usually weak. The so-called anisotropic exchange, on the other hand, is not always present, but when it is, it can be very intense. It is not really a new type of swapping: it arises from the combination of swapping interaction with spin-orbit coupling processes. The dependence in this case is more complex and in general it is not trivial to predict it, but qualitatively the consequence is the same as in the case of dipole interaction: the interaction between two magnetic moments depends not only on their relative orientation but also on their orientation. about the line that joins them.
Whatever its origin, if the Hamiltonian of Heisenberg must take into account this correction of anisotropy D→ → {displaystyle {vec {D}}}, can be expressed as:
H^ ^ =− − J⋅ ⋅ (S→ → i⋅ ⋅ S→ → j)+S→ → i⋅ ⋅ D→ → ⋅ ⋅ S→ → j{displaystyle {hat {H}}=-Jcdot ({vec {S}}cdot {cdot {vec {S}}_{j})+{vec {S}}}_{i}cdot {vec {D}}}{cdot {cd}}}_{s}
Antisymmetric Swap
I. E. Dzialoshinski recognized in 1958 that when the symmetry of the system is low, a new term appears in the Hamiltonian, using the cross product instead of the scalar, of the form:
H^ ^ DM=d→ → ⋅ ⋅ (S→ → i× × S→ → j){displaystyle {hat {H}_{DM}={vec {d}}}cdot ({vec {S}}_{i}times {vec {S}}}_{j})}
which complements the Heisenberg Hamiltonian and the anisotropic swap, resulting in:
H^ ^ =− − J⋅ ⋅ (S→ → i⋅ ⋅ S→ → j)+S→ → i⋅ ⋅ D→ → ⋅ ⋅ S→ → j+d→ → ⋅ ⋅ (S→ → i× × S→ → j){dsplaystyle {cH}=-Jcdot ({vec}{cdot {cdot {vec}}_{s}}{j}{vec {s}}{s}}{cd}{s}{cdot {d}}}{cdot {cd}}{cd}{cd}{cd}}{cd}}{cd}}{cd}}}{cd}{cd}}{cd}}{cd}{cd
The term d→ → {displaystyle {vec {d}}} is known as antisimetric exchange or as interaction of Dzialoshinski-Moriya. Its main effect is the mix between different magnetic moment states, such as a singlete and a triplet. Thus, in some anti-ferromagnetic systems, because of this interaction the fundamental state ceases to be entirely diamagnetic. The effect of the antisimetric exchange is to introduce a small tendency to dispose of the spins with a perpendicular orientation instead of parallel or antiparallel, which is known as canteo of thorn. In practice in some cases this transforms an antiferromagnetic system into what is known as an feromagneto weak, where small contributions to the magnetic moment that are not well aligned antiferromagnetically shrink to give a macroscopic magnetic moment.
Hubbard model and t-J model
The coexistence between magnetic exchange and electronic transfer is not limited to double exchange and indirect exchange. There are a whole series of systems that benefit from models that parameterize the two effects separately but take them into account simultaneously. The Hubbard model was proposed by J. Hubbard in 1963 as a model of solid-state physics to describe the behavior of electrons in narrow-band solids, and has since been used to describe transitions. phase between insulating and conducting systems. It can be written, in terms of the second quantization, as
<math alttext="{displaystyle H_{Hub}=-tsum _{,sigma }(c_{i,sigma }^{dagger }c_{j,sigma }^{}+h.c.)+Usum _{i=1}^{N}n_{iuparrow }n_{idownarrow }}" xmlns="http://www.w3.org/1998/Math/MathML">HHub=− − t␡ ␡ .i,j▪,σ σ (ci,σ σ † † cj,σ σ +h.c.)+U␡ ␡ i=1Nni↑ ↑ ni↓ ↓ {displaystyle H_{Hub}=-tsum _{cHFFFFFF00,}(c_{i,sigma }^{dagger }c_{j,sigma }{}{cHFFFFFFFF00} } ^{i }n_{iuparrow }n_{idown<img alt="{displaystyle H_{Hub}=-tsum _{,sigma }(c_{i,sigma }^{dagger }c_{j,sigma }^{}+h.c.)+Usum _{i=1}^{N}n_{iuparrow }n_{idownarrow }}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5ea15825e797151c462fe9071188b5806a981fab" style="vertical-align: -3.338ex; width:47.425ex; height:7.676ex;"/>
where t is electronic transfer, U It's orbital energy, c,c† † {displaystyle c,c^{dagger } are the operators creation and destruction, σ is the projection of thorn, n is the population operator of an orbital, and i, j They're neighboring positions on the net. As usual, it is summarized as h.c. the terms necessary for the operator's hermitity.
From this model Józef Spałek derived in 1977 the t-J model, which has been used to describe systems with high electronic correlation and has been generalized to systems with more than one orbital per atom or ion. It can be written as:
<math alttext="{displaystyle {hat {H}}_{tJ}=-tsum _{,sigma }(c_{isigma }^{dagger }c_{jsigma }+h.c.)+Jsum _{}({vec {S}}_{i}cdot {vec {S}}_{j}-n_{i}n_{j}/4)}" xmlns="http://www.w3.org/1998/Math/MathML">H^ ^ tJ=− − t␡ ␡ .i,j▪,σ σ (ciσ σ † † cjσ σ +h.c.)+J␡ ␡ .ij▪(S→ → i⋅ ⋅ S→ → j− − ninj/4){displaystyle {hat {H}_{tJ}=-tsum _{ boundi,j,sigma }(c_{isigma }{dagger }c_{jsigma } +h.c.)+Jsum _{cd}{cd}{cd}{cd}{cd}{cd}{cd}{<img alt="{displaystyle {hat {H}}_{tJ}=-tsum _{,sigma }(c_{isigma }^{dagger }c_{jsigma }+h.c.)+Jsum _{}({vec {S}}_{i}cdot {vec {S}}_{j}-n_{i}n_{j}/4)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6dbf93687842a5a688e8e0901d08c7be56dc994c" style="vertical-align: -3.338ex; width:56.827ex; height:6.009ex;"/>
In magnetochemistry it is applied to mixed valence systems.
Swap in density functional theory
In density functional theory, the exchange interaction, along with electronic correlation, is a complex problem. The basis of this theory is a functional that relates the energy of the system with the function that describes its electron density. The problem is that the exact functional for the energies corresponding to the exchange interaction and to the electronic correlation are only known for the electron gas. Starting in the 1990s, this has been tried to be solved in various ways, either by incorporating a portion of the exact exchange energy from Hartree–Fock calculations, so-called hybrid functionals, either from electron gas generalizations using the Monte Carlo method, or from the local density approximation (LDA).
On the other hand, the success of density functional theory has prompted efforts to use it to estimate the magnetic exchange parameter in model Hamiltonians describing complicated molecules, as is done with other chemistry methods quantum. For this it is necessary to overcome some limitations inherent to the theory, since it is originally developed for the ground state, or, in other words, only a Slater determinant. As early as 1984 Schwartz and Mohn proposed the basic idea of forcing concrete spin configurations and calculating the magnetic exchange from these energy differences in a Heisenberg Hamiltonian context, and multiple refinements and alternatives have since been proposed.
Contenido relacionado
Electroweak Spontaneous Symmetry Breaking
Organic chemistry
Silicon






















![{displaystyle H(mathbf {R} _{ij})={frac {{vec {I}}_{i}cdot {vec {I}}_{j}}{4}}{frac {left|Delta k_{m}k_{m}right|^{2}m^{*}}{(2pi)^{3}R_{ij}^{4}hbar ^{2}}}left[2k_{m}R_{ij}cos(2k_{m}R_{ij})-sin(2k_{m}R_{ij})right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35c5a759b778c677a3977753e773d66d3806b021)













