Rectangle

In plane geometry, a rectangle is a parallelogram whose four sides are at right angles to each other. Opposite sides have the same length. A rectangle whose four sides are the same length is a square.

The perimeter of a rectangle is equal to the sum of all its sides:

P=2⋅ ⋅ a+2⋅ ⋅ b=2⋅ ⋅ (a+b){displaystyle P=2cdot a+2cdot b=2cdot (a+b),}

The area of a rectangle is equal to the product of two of its adjacent sides:

A=b⋅ ⋅ a{displaystyle A=bcdot a}

Definition

A rectangle is a geometric figure that has four 90º interior angles. It is a parallelogram, that is, all its sides are parallel two by two.

By close genus and specific difference

The rectangle is a parallelogram with a right angle.

Proposition

The rectangle has all four right angles.

Test

By definition, it has a straight angle. Because it is a parallelogram, its opposite is also a straight angle; and the other two angles, which are supplementary to the previous two, add 180o. And as they are opposite, they are equal with each other, then each of the four is a straight angle.

Properties

Rectangle ABCD. d It's one of his two diagonals.

1. Its parallel sides are the same.
2. The two diagonals of one side rectangle a{displaystyle a} and b{displaystyle b} miden d=a2+b2{displaystyle d={sqrt {a^{2}+b^{2}}}}}.
3. Your two diagonals biweek each other in the common midpoint(this characteristic also defines it). This point is the center of the figure, in the sense that every straight that passes through it, cuts the rectangle into two equidistant points of the center, so defines a symmetry regarding a point for the points of the rectangle.
4. The rectangle has two axial symmetries, compared to axes parallel to their sides and passing through the center.
5. Any rectangle can be inscribed in a circumference, two of whose diameters match the diagonals of the rectangle.
6. Using as the basis of a triangle a base of the rectangle and the midpoint of the opposite side, as the opposite vertex, it is an isosceles triangle of area equal to half of that of the rectangle.
7. Employing as the basis of any triangle the base of the rectangle and as the opposite vertex a point that differs as the height of the rectangle, you get a family of equivalent triangles and whose vertices form a geometric place: the straight parallel to the base of the rectangle.
8. If the M, N, P, Q midpoints of a rectangle are joined, the MNPQ rombo is generated through segments.

Theorems

1. The isoperimetry theorem for rectangles states that among all rectangles with a given perimeter, the square is the one with the largest area.
2. A parallelogram with equal diagonals is a rectangle.
3. The Japanese theorem for cyclic quadrilateral establishes that the incentres of four triangles determined by the vertices of a cyclic quadrilateral taken from three in three form a rectangle.

Symmetry

1. The two straight lines perpendicular to each other, parallel to the contiguous sides and passing through the center of the rectangle, are axial symmetry axial to the points of the rectangle.
2. The center of the rectangle (intersection of the diagonals) is the center of central symmetry of the points of the rectangle.

Rectangles with proper names

Rectangle aureum.

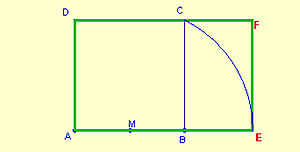
• The aureous rectanglealso called a rectangle of gold or rectangle ≈It's the rectangle whose sides are in golden reason. If b and h are the sides, b/h = δ. To build it from a square of AB side, it is enough to determine the M midpoint of one of the AB sides, and to draw, with center in point M, a circle that passes through one of the C vertices on the opposite side.

Graphical representation of an orthoedron that generalizes the construction of a rectangle, in the three-dimensional euclide space.

• Rectangle 2{displaystyle {sqrt {2}}} (root rectangle 2), the one whose relationship between base and height is equal to the square root of two. If b and h are sides, b/h = 2{displaystyle {sqrt {2}}}. The interest of this rectangle is that if it is divided into two halves, on its longest side, the two new rectangles obtained maintain exactly the same proportion as the original, that is, they are also rectangles root of 2. This is why, among other uses, it is the format used to measure paper sheets according to the DIN 476 and ISO 216 standards.

Construction starting from the square: in a similar way to the golden rectangle, a circle is drawn with its center at point A, which passes through the opposite vertex C.

• Double square, the one whose sides are in relation 2:1.
• Television screens. Until the introduction of high-definition monitors, whose usual [ancho:high] ratio is [16:9], conventional television systems used rectangles with the ratio [4:3]. Since these proportions are fixed, it is enough to know the measurement of the diagonal (normally expressed in inches) to establish the size of the screen.

Geometric magnitudes for a rectangle

Given a two-dimensional figure, the centered n-moments of area can be defined as:

Mx1...... xn(n)=∫ ∫ Ax1...... xndA{displaystyle M_{x_{1}dots x_{n}}}^{(n)}=int _{A}x_{1}dots x_{n}dA}

The 0-moment matches the area, the two 1-moments are called first moments of area (or static moments) Sx=Mx(1),Sand=Mand(1){displaystyle scriptstyle S_{x}=M_{x}^{(1)}, S_{y}=M_{y}{y^{(1)}} are null for any flat figure. The 2-moments are called second moments of area (or moments of flat inertia) and for a rectangle are:

Ixx=Mxx(2)=bh312,Iandand=Mandand(2)=hb312,Ixand=Iandx=Mxand(2)=0{displaystyle I_{xx}=M_{xx}{(2)}={frac {bh^{3}}{12}}}},quad I_{yy}=M_{yyy}{{(2)}={{frac {hb^{3}}{12}}}}{quad I_{xy}=

Where b is the base of the rectangle and h its height.

Crossed rectangles

Generation of crossed rectangles

A crossed (i.e., self-intersecting) quadrilateral consists of two opposite sides of a quadrilateral together with their two diagonals (see antiparallelogram). Similarly, a crossed rectangle is a crossed quadrilateral made up of two opposite sides of a rectangle together with their two diagonals. It has the same arrangement of vertices as the rectangle. It appears as two identical triangles with a common vertex. The geometric intersection is not considered a proper vertex.

A crossed quadrilateral sometimes resembles a bow tie or a butterfly. A rectangular wire frame takes the shape of a crossed quadrilateral when its short sides are rotated in three-dimensional space in opposite directions. A crossed rectangle is sometimes also referred to as a 'corner eight'.

The interior of a crossed rectangle can have a polygon density of ±1 in each triangle, depending on the orientation (clockwise or counterclockwise) with which they are traversed.

A crossed rectangle is not equiangular. The sum of its interior angles (two acute and two obtuse), as in any crossed quadrilateral, is 720°.

A rectangle and a crossed rectangle are quadrilaterals with the following characteristics in common:

• The opposite sides have the same length.
• The two diagonals have the same length.
• It has two lines of reflection symmetry and rotational symmetry of order 2 (180°).

Other rectangles

A saddle has 4 non-coplanary vertices (the alternating vertices of an orthoedron). It is an interior minimal surface defined as a linear combination of the 4 vertices. This example shows 4 blue sides of the rectangle, and the two diagonals in green colour, all diagonals of the rectangular faces of the orthoedron.

In spherical geometry, a spherical rectangle is a figure whose four sides are arcs of great circles, its four angles are equal and greater than 90°, and its opposite arcs have the same length.

In elliptic geometry, an elliptical rectangle is a figure in the elliptical plane whose four edges are elliptical arcs, which intersect with angles equal to and greater than 90°, and their opposite arcs have the same length.

In hyperbolic geometry, a hyperbolic rectangle is a figure in the hyperbolic plane whose four edges are hyperbolic arcs intersecting with four equal angles less than 90°, and whose opposite arcs have the same length.

Tessellations

The rectangle is used in many periodic tiling patterns, such as these tiles:

Stacked union.

Displaced union.

Strapped basket.

Strapped basket.

Fish thorn.

Square, perfect, and other rectangles

A rectangle can be tiled using squares, rectangles, or triangles. The coating is said to be Perfect if all tiles are alike, you have a finite number of tiles, and no two tiles are the same size. If two of these tiles are the same size, the coating is said to be imperfect. In a triangulated perfect (or imperfect) cover, the triangles must be right.

A rectangle has commensurable sides if and only if it can be covered by a finite number of distinct squares. The same is true if the tiles are unequal isosceles triangles.

The coverings of rectangles with other geometric shapes that have attracted the most attention are those of congruent non-rectangular polyominoes, allowing for all rotations and reflections. There are also tiled by means of congruent polyabolos.