Quantum electrodynamics
Quantum Electrodynamics (EDC or QED as an acronym for Quantum Electrodynamics) is the quantum theory of the electromagnetic field. This theory describes phenomena involving electrically charged particles interacting by means of the electromagnetic force.
History and predictions
Quantum electrodynamics is one of the most precise quantum theories to be created in the 20th century. It is capable of making predictions of certain physical quantities with up to twenty decimal places of precision, a rare result in earlier physical theories. For that reason the theory was called "the jewel of physics." Among his most accurate predictions are:
- The abnormal magnetic moment of the electron and the muon, for which the equation of Dirac predicted a value of exactly the double of the classic value. For the electron the EDC predicts a value:
ge=2(1+a)=2(1+qe24π π ε ε 0hc){displaystyle g_{e}=2(1+a)=2left(1+{frac {q_{e}^{2}}{4pi epsilon _{0}hc}}}}{right)}
Where:
- qe{displaystyle q_{e};} It's the electric charge of the electron.
- h{displaystyle h;} It's Planck's constant.
- c{displaystyle c;} is the speed of light in the void.
- ε ε 0{displaystyle epsilon _{0};} is the electric permitivity of the vacuum.
- The value of the Lamb displacement in the energetic levels of the hydrogen atom.
Shin'ichirō Tomonaga, Julian Schwinger, and Richard Feynman received the 1965 Nobel Prize in Physics for their development, their contributions involving a covariant prescription and gauge invariance for the computation of observable quantities. Feynman's mathematical technique, based on his diagrams, initially seemed very different from the field-theoretical approach, based on Schwinger and Tomonaga operators, but its equivalence was later shown. The renormalization procedure for making sense of some of the infinite predictions of quantum field theory also found its first successful implementation in quantum electrodynamics.
Description of the theory
Quantum electrodynamics is a detailed description of the interaction between photons and charged particles of the fermionic type. Quantum theory shares certain features with the classical description. According to the description of classical optics, light travels on all allowed paths, and its interference determines the wave fronts that propagate according to Fermat's principle. Similarly, in the quantum description of photons (and fermions), they pass through every possible path allowed by apertures or optical systems. In both cases the observer simply detects the mathematical result of the superposition of all the waves considered along line integrals. One difference is that in electrodynamics the effective speed of a photon can exceed the speed of light on average.
In addition, quantum electrodynamics was the first quantum field theory in which the difficulties of constructing a complete description of fields and of the creation and annihilation of quantum particles were satisfactorily resolved.
Formalism
Mathematically, we can say that quantum electrodynamics have the structure of an abelian gauge theory, being the group of gauge associated in unit group U(1){displaystyle scriptstyle mathrm {U} (1)}. The gauge field that mediates the interaction between fields of spin -1/2 with load is the electromagnetic field.
The temporal evolution of a system of charged particles and photons can be calculated by means of a perturbative calculation. Specifically, the comparison with the experiments that can be carried out frequently requires the calculation of the elements of the matrix S that allow finding the cross sections of dispersion for the particle that can be compared with the results of the experiments.
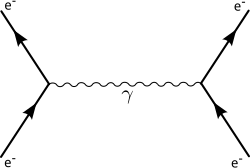
Quantum electrodynamics reduces this type of calculation to a perturbative expansion in power series that allows finding those effective sections with the desired precision. Each of the perturbative terms admits a graphical representation known as a Feynman diagram. In fact, quantum electrodynamics was historically the first theory where Feynman diagrams were used to aid perturbative calculation. The shape of each of the perturbative terms and, therefore, the associated graphical representation depends on the shape of the Lagrangian that characterizes said theory (see below).
Local gauge invariance OR ( 1 ) {displaystyle mathrm {U} (1)}
It is interesting to note how the EDC lagrangian can be found as a simple requirement that the lagrangian of a free fermion with non-null electric charge be invariant local gauge. Sea Ll{displaystyle {mathcal {L}}_{l}} the lagrangian of free fermion:
Ll=ı ı ! ! END END ! ! γ γ μ μ ▪ ▪ μ μ END END − − mEND END ! ! END END =END END ! ! (ı ı ! ! γ γ μ μ ▪ ▪ μ μ − − m)END END {displaystyle {mathcal {L}}_{l}={dot {imath }{bar {psi }}{gamma ^{mu }partial _{mu }{m{bar {psi }{bar {psi }{dot {imath partial}{m{
In other words, we want to Ll{displaystyle {mathcal {L}}_{l}} be invariant under a local transformation U(1){displaystyle mathrm {U} (1)} so the field changes like:
END END (x)→ → e− − ı ı ! ! α α (x)END END (x){displaystyle psi (x)rightarrow e^{-{dot {imath }alpha (x)}psi (x)}
In that case, the covariant derivative and the gauge will be:
Dμ μ =▪ ▪ μ μ − − ı ı ! ! eAμ μ ▪ ▪ Aμ μ → → Aμ μ − − 1e▪ ▪ μ μ α α {displaystyle D_{mu }=partial _{mu }-{dot {imath }}eA_{mu }qquad therefore qquad A_{mu }rightarrow A_{mu }-{frac {1}}{partial _{mu }alpha }}}
With all this, we are left with the Lagrangian of quantum electrodynamics:
LQED=END END ! ! (ı ı ! ! γ γ μ μ ▪ ▪ μ μ − − m)END END +eEND END ! ! γ γ μ μ Aμ μ END END − − 14Fμ μ .. Fμ μ .. {displaystyle {mathcal {L}}_{QED}={bar {psi }left({dot {imath }gamma ^{mu }partial _{mu }-mright)psi +e{bar {psi }{gamma ^{mu fra}{mu с}{
Experimental Adequacy
It is important to note that quantum electrodynamics does not give concrete values of what would happen in a certain experiment, but only probabilities of a certain type of situation happening. That is why the experiments use a relatively large number of particles that are statistically scattered according to the probabilities predicted by the theory. From the distribution of dispersed particles, the cross section can be measured, comparable to the numerical predictions of the theory.
The predictions of quantum electrodynamics have been confirmed by experiments to an unusual level of precision: you usually have experiments that agree to 12 decimal places correctly with the theory's predictions. This makes the quantum EDC the most accurate theory built by humans.
Mathematical formulation
The dynamics and basic properties of a field theory depend on the form selected for the Lagrangian. The selection of the Lagrangian depends on the symmetries of the gauge group and on the fact that the theory adequately describes the interaction between charged fermions. In a theory that describes fermionic fields interacting through a bosonic gauge field associated with massless particles (photons) whose gauge group is commutative, the starting Lagrangian can be taken as:
(1)L=iEND END ! ! γ γ μ μ ▪ ▪ μ μ END END − − eEND END ! ! γ γ μ μ Aμ μ END END − − mEND END ! ! END END − − 14Fμ μ .. Fμ μ .. {displaystyle {mathcal {L}}=i{bar {psi }}{gamma ^{mu}partial _{mu }psi -e{bar {psi }}}{gamma _{mu }A^{mu }{mu }{bar {psi }{fr}{f}{
Where the Ferminonic Field END END {displaystyle psi } and his deputy Dirac END END ! ! {displaystyle {bar {psi}}} are the fields that represent electrical load particles, specifically the electron and the positron fields represented as Dirac's thorn. The part of the lagrangian that contains the electromagnetic field tensor describes the free evolution of the electromagnetic field, while the Dirac equation with the covariant gauge derivative describes the free evolution of the fields of the electromagnetic and positron as well as its interaction with the electromagnetic field.
Equations of Motion
The equations of "motion" or equations of time evolution of quantum electrodynamics can be obtained by means of the Euler-Lagrange equations of the Lagrangian of the theory. Inserting this Lagrangian into the Euler-Lagrange equations, the time evolution equation of the theory is obtained:
(2)▪ ▪ μ μ (▪ ▪ L▪ ▪ (▪ ▪ μ μ END END ))− − ▪ ▪ L▪ ▪ END END =0with{▪ ▪ μ μ (▪ ▪ L▪ ▪ (▪ ▪ μ μ END END ))=▪ ▪ μ μ (iEND END ! ! γ γ μ μ )▪ ▪ L▪ ▪ END END =− − eEND END ! ! γ γ μ μ Aμ μ − − mEND END ! ! {cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF00} {cHFFFFFF00}{cHFFFFFFFF00}{cHFFFFFFFF00} {cHFFFFFFFFFFFF}{cHFFFFFF}{cHFFFFFFFF00} {cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Placing the two terms inside the Euler-Lagrange equation finally results in the following evolution equation for the fermionic field:
iγ γ μ μ ▪ ▪ μ μ END END − − mEND END =eγ γ μ μ Aμ μ END END {displaystyle igamma ^{mu }partial _{mu }psi -mpsi =egamma _{mu }A^{mu }psi ,}
The member on the left is precisely the Dirac equation and the term on the right represents the interaction with the electromagnetic field.
The same equations of Euler-Lagrange, now applied to the field Aμ μ {displaystyle A^{mu }, allow to find the evolution equations of the electromagnetic field:
(3)▪ ▪ .. (▪ ▪ L▪ ▪ (▪ ▪ .. Aμ μ ))− − ▪ ▪ L▪ ▪ Aμ μ =0with{▪ ▪ .. (▪ ▪ L▪ ▪ (▪ ▪ .. Aμ μ ))=▪ ▪ .. (▪ ▪ μ μ A.. − − ▪ ▪ .. Aμ μ )▪ ▪ L▪ ▪ Aμ μ =− − eEND END ! ! γ γ μ μ END END ##### ###########################################################################################################################################################################################################################################################
And the evolution equation of the electromagnetic field is finally:
▪ ▪ .. F.. μ μ =eEND END ! ! γ γ μ μ END END {displaystyle partial _{nu }F^{nu mu }=e{bar {psi }{gamma ^{mu }psi ,}
Where the right hand side can be interpreted as the current density associated with the fermionic field.
Feynman's Rules
To account for all quantum effects, it is necessary to replace the components of the fields in the previous differential equations by interpretable self-adjunct operators as genuine quantum operators. In general, this leads to equation systems that we don't know how to integrate exactly, but that support disruptive treatment, decompose the temporary evolution operator U^ ^ QED=Exp (itH^ ^ QED){displaystyle {hat {U}_{QED}=exp(it{hat {H}_{QED}}})} in power series or disturbing series.
The calculation of each term of the previous series can be done almost automatically with the help of the so-called Feynman diagrams, to which some Feynman rules can be associated. The precision of the calculation depends on how many terms are considered in the previous perturbative series.
Renormalization
A serious problem with Feynman's rules is that as they were first stated they lead to divergent diagrams and terms in the perturbative series, that is, non-finite terms that mess up the computation of finite terms. Obviously all physical results are finite and these divergent terms of the calculation are not observable in reality. Renormalization is a set of additional rules that interpret what relationship exists between the calculated terms and the measurable terms in reality and generate additional rules that allow calculations to be "normalized" and ensure that finite numerical results comparable to reality are produced by experiment.
It is known that the fact that a quantum theory is a gauge field theory gives it the property of being renormalizable, in the sense that there is a set of additional rules that allow unobservable divergent terms to be eliminated and give rise to finite results.
Contenido relacionado
Leon Foucault
Energy-momentum tensor
Robert Andrews Millikan