Quadrilateral

ImprimirCitar

In Euclidean plane geometry, a quadrilateral is a polygon with four edges and four vertices (or colloquially, with four sides and four corners). Sometimes the term quadrangle is used by analogy with triangle, as well as tetragon for consistency with pentagon (5 sides), hexagon (6 sides), and in general, with polygons with n sides (in this case, with n=4 sides).

The word quadrilateral is derived from the Latin words "quadri", a variant of four, and "latus", meaning "side& #3. 4;

Quadrilaterals are simple (non-self-intersecting) or complex (self-intersecting) polygons, also called crossed. Simple quadrilaterals can also be classified as convex or concave.

The interior angles of a simple (and flat) quadrilateral ABCD add up to 360 degrees, that is

{displaystyle angle A+angle B+angle C+angle D=360^{circ }.}

It is a special case of the formula for the sum of the interior angles of an n-gon, whose value is (n-2)×180°.

All quadrilaterals whose sides do not intersect each other automatically overlap the plane by repeatedly rotating about the midpoints of their sides.

Elements of a quadrilateral

The elements of a quadrilateral are the following:

4 vertices: intersection points of the sides that make up the quadrilateral.
4 sides: segments that unite the adjacent vertices.
2 diagonals: segments whose ends are two non-contiguous vertices.
4 inner angles: the determined by two contiguous sides.
4 outer angles: the one determined by the prolongation of one side on a vertex and the contiguum on the same vertex.
An incenter, center of the circle inscribed.
The sum of its inner angles is equal to 360o

General propositions

Nomenclature of the elements of a quadrilateral

The quadrilateral have two diagonals.
The diagonals of a quadrilateral are cut into an inner point, if and only if this is convex.
They have four angles.
The sum of the measurements of the angles of a quadrilateral ${displaystyle ABCD}$ convexo is 360o or 2π radianes.

{displaystyle angle A+angle B+angle C+angle D=360^{circ }}

If a quadrilateral is inscribed in a circumference the sum of the measure of its opposite angles is equal to 180o.
Be ABCD a quadrilateral registered in a diameter circle $AB$ , then the projections of the AD and BC sides on the CD straight are equal.
The area of a registered quadrilateral is obtained with the formula ${displaystyle A={sqrt {(p-a)(p-b)(p-c)(p-d)}}}$ where a, b, c, d are the sides and p is the semiperimeter.
If the midpoints of all sides of a quadrilateral are joined with four segments, then these segments form a parallelogram.
If a quadrilateral is circumscribed then the sum of its opposite sides are equal. ${displaystyle AB+CD=BC+DA}$ .
For a convex quadrilateral is fulfilled ${displaystyle a^{2}+b^{2}+c^{2}+d^{2}=d_{1}^{2}+d_{2}^{2}+4m^{2}}$ where ${displaystyle a,b,c,d}$ are the sides; ${displaystyle d_{1},d_{2}}$ the diagonal and m, the length of the segment linking the midpoints of the diagonals.
It is also verified: ${displaystyle d_{1}^{2}+d_{2}^{2}=m_{1}^{2}+m_{2}^{2}}$ where ${displaystyle d_{1},d_{2}}$ It's the diagonals and ${displaystyle m_{1},m_{2}}$ are segments, which unite the middle points of opposite sides, called simedians.

Classification

Types of Paralelogramos

Deltoid

Quadrilaterals are classified according to the parallelism of their sides, their lengths and their interior angles:

Paralelogram: its opposite sides are parallel.
- Square: all its sides are equal, all its inner angles are straight, its diagonals are equal and perpendicular to each other, it has an inscribed circle and another circumscribed, and all the squares are similar to each other.
- Rombo: all its sides are equal, each pair of sharp and obtused angles are opposite, its diagonals are different and perpendicular to each other, are bisectrices, has an inscribed circle.
- Rectangle: its opposite sides are equal two to two and the parallels, all its inner angles are straight, its two diagonals are equal but are not perpendicular to each other and has a circumscribed circumference.
- Romboide: its opposite sides are equal two to two, each pair of sharp and obtusous angles are opposite, its two diagonals are of different length and are not perpendicular to each other.
Trapecio: In geometry, it is called trapezecio to a quadrilateral that has two parallel non-secure sides called bases of the trapeze, and the perpendicular segment between the two bases and its own length are called height of the trapeze
Trapezoid: In flat euclide geometry, a trapezoid is a convex quadrilateral without parallel sides.

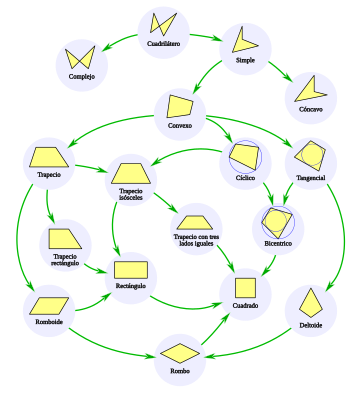
Nomenclature of quadrilaterals

In the illustrative graphic of the taxonomy of quadrilaterals, we go from the most general definitions to the most specific ones following the direction of the arrows.

This is how we start from a quadrilateral defined as a closed polygon with four sides, without further restrictions, to then differentiate compound quadrilaterals from simple ones.

In a complex quadrilateral, two of its sides intersect. In a simple one the sides do not intersect.

Simple quadrilaterals are divided into:

Concavos. In a concave quadrilateral at least one of its inner angles is more than 180°.
Convexes. A convex quadrilateral has no inner angles that measure more than 180°. The general convex quadrilateral would be the trapezoid. Convexes are subdivided into:

Cyclic quadrilateral, if you can trace a circumference that passes through its vertices.
Tangential quadrilateral, if you can trace a tangent circle to each side.
Traps, if they have two side parallels. They differ:
1. Romboide, as a more general case of parallelogram, if the sides are parallel two to two.
2. Trapecio rectangle, which has a perpendicular side to its bases.
3. Trapecio isosceles, whose unparalleled sides are of equal measure. This trapeze is also cyclic.

A quadrilateral that is both cyclic and tangential is called a bicentric quadrilateral. The deltoid is tangential with two pairs of equal sides.

A particular case of an isosceles trapezoid is when the length of one of the bases is the same as that of its sides, for which reason a trapezoid with three equal sides is configured.

Simple quadrilaterals

Euler diagram of various types of simple quadrilateral

Any quadrilateral that does not self-intersect is a simple quadrilateral.

Convex Quadrilaterals

In a convex quadrilateral, all interior angles are less than 180° and the two diagonals lie inside the quadrilateral. Trapezoid or irregular quadrilateral: none of its sides are parallel to each other

Trapecio: At least a couple of opposite sides are parallel. Traps include parallels.
Trapecio isosceles: A pair of opposite sides are parallel and the angles of each base are equal with each other. Other alternative definitions are: a quadrilateral with a symmetry axis that divides a pair of opposite sides; or a trapeze with diagonals of equal length.
Paralelogram: A quadrilateral with two pairs of parallel sides. The equivalent conditions are that the opposite sides are of equal length; that the opposite angles are equal; or that the diagonals bise with each other (i.e., they are cut in their midpoints). To the set of parallelograms belong the rombos (including those that have their right angles, that is, the squares) and the romboids (including those that have their right angles, the rectangles). In other words, parallelograms include all romboids and all rombos, and therefore also include all rectangles and all squares.
Rombo: Its four sides have the same length. An equivalent condition is that the diagonals are biased perpendicularly with each other. Informally: "a square scaled" (but strictly, including a square as well).
Romboide: A parallelogram in which the adjacent sides have different lengths and some of their angles are oblique (equivalently, without straight angles). Informally: "a chisel rectangle." Not all references agree, and some define a romboid as a parallelogram that is not a rombo.
Rectangle: Its four angles are straight angles. An equivalent condition is that the diagonals are cut together and that the four resulting segments have the same length. Rectangles include squares.
Square (regular quadrilateral): Its four sides have the same length (it is equilateral) and the four angles are straight angles. An equivalent condition is that the opposite sides are parallel (a square is a parallelogram), that the diagonals bise perpendicularly between themselves and have the same length. A quadrilateral is a square if and only if it is both a rombo and a rectangle (four equal sides and four equal angles).
Oblongo: It is a term that is sometimes used in English-language texts to call a rectangle that has uneven adjacent sides (i.e., to refer strictly to a rectangle than No. It's a square.).
Deltoide: It has two pairs of adjacent sides of equal length. This implies that a diagonal divides the deltoid into two congruent parts, so the angles between the two pairs of uneven sides are equal in measure. It also implies that diagonals are perpendicular to each other. Detoids also include rombos.

Circulated Quadratum: The four sides are tangent to an inscribed circle. A convex quadrilateral is tangential if and only if the sums of the lengths of the opposite sides are equal to each other.
Tangential Trapecy: It is a trapeze in which the four sides are tangent to an inscribed circumference.
Cyclic Quadratum: The four vertices are found in a circumscribed circle. A convex quadrilateral is cyclic if and only if the opposite angles are 180°.
Right Deltoid: A deltoid with two opposite straight angles. It's a type of cyclic quadrilateral.
Harmonic Quadrel: The products of the lengths of the opposite sides are equal. It's a type of cyclic quadrilateral.
Bicentric quadrilateral: It is tangential and cyclical at the same time.
Orthodiagonal Quadratum: Its diagonals cross in a straight angle.
Ecydiagonal Quadratum: Diagonals are of equal length.
Extangenial quadrilateral: The four extensions of the sides are tangent to a circumference inscribed and exinscribed in a triangle.
Cycleaner: It is the one who has two opposite sides that, when they spread, are at 60°.
Watt Quadratum: It has a pair of opposite sides of equal length.
Quadratic Quadratum: It is a convex quadrilateral whose four vertices are found in the perimeter of a square.
Diameter quadrilateral: That cyclic quadrilateral that has one of its sides as a diameter of its circumscribed circle.
Hjelmslev Quadratum: It is a quadrilateral with two straight angles in opposite vertices.

Concave Quadrilaterals

In a concave quadrilateral, one interior angle is greater than 180° and one of the two diagonals lies outside the quadrilateral.

A dardo (or arrowhead) is a concave quadrilateral with bilateral symmetry as a deltoid, but with an inner angle greater than 180°.

Complex Quadrilaterals

An antiparalelogram

A self-intersecting quadrilateral can be called a cross quadrilateral, butterfly quadrilateral, or bow tie. In a crossed quadrilateral, the four interior angles on each side of the crossing (two acute and two obtuse, all to the left or all to the right as the figure is drawn) add up to 720°.

A cross trapeze is a self-intersecting quadrilateral in which (as in the case of a trapeze), a pair of un adjacent sides are parallel to each other.
Antiparalelogram: It is a cross quadrilateral in which (as in a parallelogram) each pair of un adjacent sides have the same length.
Crossing Rectangle: It is an anti-paralelogram whose sides are two opposite sides and the two diagonals of a rectangle, and therefore have a pair of opposite sides parallel.
Cross Square: This is a special case of a cross rectangle, where two sides are crossed in a straight angle.

Symmetrical Quadrilaterals

Convex quadrilateral according to their symmetries

Quadrilaterals can also be classified according to their symmetry properties:

Simple Quadrilaterals

Axes of symmetry:

4 Axes: the square has four axes of symmetry: its two diagonals and its two bimedians
2 Axes: the rombo (their two diagonals) and the rectangle (their two bimedians)
1 Axis: the isosceles trapeze (the bimedian between the two parallel faces) and the deltoid, both concave and convex (a diagonal)

Rotational symmetry:

The square is isotoxal with 90° twists.
Rombo and rectangle are isotoxal with respect to 180° spins.

These criteria are also applicable to complex quadrilaterals:

Complex Quadrilaterals

Axes of symmetry:

2 Axes: the antiparalelograms of the square and the rectangle have two axes: a bimedian and its perpendicular through the center.
1 Axis: the antiparalelogram of the isosceles trapeze is symmetrical to the bimedian between the parallel faces.

Rotational symmetry:

The anti-paralelograms of the square and the rectangle are isotoxal with 180° spins.

The rest of the quadrilaterals lack symmetries.

Diverse formulas

The four sides of a quadrilateral: a, b, c, d;
the four vertices: A, B, C, D;
the two diagonals: e, f.

The sum of the internal angles is equal to 360°:

{displaystyle alpha +beta +gamma +delta =360^{circ }}

If diagonals are perpendicular, the following relationship is fulfilled:

{displaystyle theta =90^{circ }Longleftrightarrow a^{2}+c^{2}=b^{2}+d^{2}}

The area of a quadrilateral can be calculated by any of these six formulas:

{displaystyle A={frac {efsin theta }{2}}}

{displaystyle A={frac {adsin alpha +bcsin gamma }{2}}={frac {absin beta +cdsin delta }{2}}}

{displaystyle A={frac {1}{4}}left(b^{2}+d^{2}-a^{2}-c^{2}right)tan theta }

{displaystyle A={frac {1}{4}}{sqrt {4e^{2}f^{2}-left(b^{2}+d^{2}-a^{2}-c^{2}right)^{2}}}}

{displaystyle A={frac {1}{2}}{sqrt {|{vec {e}}|^{2}|{vec {f}}|^{2}-({vec {e}}cdot {vec {f}})^{2}}}}

${displaystyle A={tfrac {1}{2}}adcdot sin {alpha }+{tfrac {1}{4}}{sqrt {4b^{2}c^{2}-(b^{2}+c^{2}-a^{2}-d^{2}+2adcdot cos {alpha })^{2}}}}$ (for a quadrilateral with concavity in C change the first sign + per -).

Archimedes-Faure theorem

Let be the inscribed quadrilateral with sides a,b,c and d; of perpendicular diagonals that, when intersecting, determine the segments m and n in one of them, and p and q in the other, and whose radius of the circumcircle is called R. In such a case, the following equalities are valid:

${displaystyle a^{2}+c^{2}=b^{2}+d^{2}=4R^{2}}$

(1) ${displaystyle m^{2}+n^{2}+p^{2}+q^{2}=4R^{2}}$

Special segments

The two diagonals of a convex quadrilateral are the segments connecting opposite vertices.

The two bimedians of a convex quadrilateral are the line segments connecting the midpoints of opposite sides. They intersect at the centroid of vertices of the quadrilateral.

The four m-heights of a convex quadrilateral are the perpendiculars to one side through the midpoint of the opposite side.

Area of a convex quadrilateral

There are several general formulas for the area K of a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD and >d = DA.

Trigonometric Formulas

The area can be expressed in trigonometric terms as

{displaystyle K={tfrac {1}{2}}pqcdot sin theta}

where the lengths of the diagonals are p and q and the angle between them is θ. In the case of an orthodiagonal quadrilateral (e.g., rombo, square or deltoid), this formula is reduced to ${displaystyle K={tfrac {1}{2}}pq}$ since θ It's 90°.

The area can also be expressed in terms of the bimedians as

{displaystyle K=mncdot sin varphi}

where the lengths of the bimedians are m and n and the angle between them is φ.

The Bretschneider formula expresses the area in terms of the length of the sides and the value of two opposite angles:

{displaystyle {begin{aligned}K&={sqrt {(s-a)(s-b)(s-c)(s-d)-{tfrac {1}{2}}abcd;[1+cos(A+C)]}}\&={sqrt {(s-a)(s-b)(s-c)(s-d)-abcdleft[cos ^{2}left({tfrac {A+C}{2}}right)right]}}end{aligned}}}

where the sides (named consecutively) are a, b, c, and d, where s is the semiperimeter, and where A and C are two (in fact, any two) opposite angles. This reduces to Brahmagupta's formula for the area of a cyclic quadrilateral when A + C = 180°.

Another formula for the area as a function of the length of the sides and the value of the angles, with the angle C between the sides b and c, and A between the sides a and d, is

{displaystyle K={tfrac {1}{2}}adcdot sin {A}+{tfrac {1}{2}}bccdot sin {C}.}

In the case of a cyclic quadrilateral, the last formula becomes ${displaystyle K={tfrac {1}{2}}(ad+bc)sin {A}.}$

In a parallelogram, where both pairs of opposite sides and angles are equal, this formula is reduced to ${displaystyle K=abcdot sin {A}.}$

Alternatively, the area can be determined in terms of the sides and the angle of intersection θ of the diagonals, as long as this angle is not 90°:

{displaystyle K={frac {|tan theta |}{4}}cdot left|a^{2}+c^{2}-b^{2}-d^{2}right|.}

In the case of a parallelogram, the last formula becomes ${displaystyle K={tfrac {1}{2}}|tan theta |cdot left|a^{2}-b^{2}right|.}$

Another area formula that includes the sides a, b, c and d, is:

{displaystyle K={tfrac {1}{2}}{sqrt {((a^{2}+c^{2})-2x^{2})((b^{2}+d^{2})-2x^{2})}}sin {varphi }}

where x is the distance between the midpoints of the diagonals and φ is the angle between the bimedians.

The last trigonometric area formula that includes the sides a, b, c, and d and the angle α between a and b, is:^{[citation needed]}

{displaystyle K={tfrac {1}{2}}abcdot sin {alpha }+{tfrac {1}{4}}{sqrt {4c^{2}d^{2}-(c^{2}+d^{2}-a^{2}-b^{2}+2abcdot cos {alpha })^{2}}},}

which can also be used for the area of a concave quadrilateral (which has the concave part opposite angle α) simply by changing the first + sign to a -.

Non-Trigonometric Formulas

The following two formulas express the area in terms of the sides a, b, c and d; of the semiperimeter s and of the diagonals p and q:

{displaystyle K={sqrt {(s-a)(s-b)(s-c)(s-d)-{tfrac {1}{4}}(ac+bd+pq)(ac+bd-pq)}},}

{displaystyle K={tfrac {1}{4}}{sqrt {4p^{2}q^{2}-left(a^{2}+c^{2}-b^{2}-d^{2}right)^{2}}}.}

The first reduces to Brahmagupta's formula in the case of the cyclic quadrilateral, since then pq = ac + bd.

Area can also be expressed in terms of the bimedians m and n; and of the slashes p and q:

{displaystyle K={tfrac {1}{2}}{sqrt {(m+n+p)(m+n-p)(m+n+q)(m+n-q)}},}

{displaystyle K={tfrac {1}{2}}{sqrt {p^{2}q^{2}-(m^{2}-n^{2})^{2}}}.}

In fact, three of the four values m, n, p and q are sufficient for the determination of the area, as in any quadrilateral the four values are related by ${displaystyle p^{2}+q^{2}=2(m^{2}+n^{2}).}$ The corresponding expressions are:

{displaystyle K={tfrac {1}{2}}{sqrt {[(m+n)^{2}-p^{2}]cdot [p^{2}-(m-n)^{2}]}},}

if the lengths of two bimedians and one diagonal are given, and

{displaystyle K={tfrac {1}{4}}{sqrt {[(p+q)^{2}-4m^{2}]cdot [4m^{2}-(p-q)^{2}]}},}

if the lengths of two diagonals and one bimedian are given.

Vector Formulas

The area of a quadrilateral ABCD can be calculated using vectors. Let the vectors AC and BD correspond to the diagonals from A to C and from B through D. The area of the quadrilateral is then

{displaystyle K={tfrac {1}{2}}|mathbf {AC} times mathbf {BD} |,}

which is half the magnitude of the vector product of the vectors AC and BD. In two-dimensional Euclidean space, expressing the vector AC as a free vector in Cartesian space equal to (x₁, y₁) and BD as (x₂, y₂), this can be rewritten as:

{displaystyle K={tfrac {1}{2}}|x_{1}y_{2}-x_{2}y_{1}|.}

Diagonals

Properties of diagonals in some quadrilaterals

The following table lists whether the diagonals in some of the most basic quadrilaterals bisect each other, whether their diagonals are perpendicular, and whether their diagonals have the same length. The list applies to the most general cases:

Quadrel	Bisecrate diagonals	Perpendicular diagonals	Equal diagonals
Trapecio	No.	See note 1	No.
Trapecio isosceles	No.	See note 1	Yes.
Paralelogram	Yeah.	No.	No.
Deltoide	See note 2	Yeah.	See note 2
Rectangle	Yes.	No.	Yes.
Rombo	Yes.	Yes.	No.
Square	Yes.	Yes.	Yes.

Note 1: Trapezoids (including isosceles trapezoids), in general do not have perpendicular diagonals, but there are an infinite number of trapezoids (not similar to each other) and isosceles trapezoids, which have perpendicular diagonals and are not no other type of quadrilateral.

Note 2: In a deltoid, one diagonal divides the other. The most general deltoid has unequal diagonals, but there are an infinite number of (non-similar) deltoids in which the diagonals are the same length (and which do not fit the definition of another quadrilateral).

Lengths of diagonals

The lengths of the diagonals in a convex quadrilateral ABCD can be calculated using the cosine rule in every triangle formed by a diagonal and two sides of the quadrilateral. So

{displaystyle p={sqrt {a^{2}+b^{2}-2abcos {B}}}={sqrt {c^{2}+d^{2}-2cdcos {D}}}}

and

{displaystyle q={sqrt {a^{2}+d^{2}-2adcos {A}}}={sqrt {b^{2}+c^{2}-2bccos {C}}}.}

Other, more symmetrical formulas for the lengths of the diagonals are:

{displaystyle p={sqrt {frac {(ac+bd)(ad+bc)-2abcd(cos {B}+cos {D})}{ab+cd}}}}

and

{displaystyle q={sqrt {frac {(ab+cd)(ac+bd)-2abcd(cos {A}+cos {C})}{ad+bc}}}.}

Generalizations of the Parallelogram Law and Ptolemy's Theorem

In any convex quadrilateral ABCD, the sum of the squares of the four sides is equal to the sum of the squares of the two diagonals plus four times the square of the length of the segment connecting the two diagonals. midpoints of the diagonals. So

{displaystyle a^{2}+b^{2}+c^{2}+d^{2}=p^{2}+q^{2}+4x^{2}}

where x is the distance between the midpoints of the diagonals. This is sometimes known as Euler's quadrilateral theorem and is a generalization of the parallelogram law.

The German mathematician Carl Anton Bretschneider deduced in 1842 the following generalization of Ptolemy's Theorem regarding the product of diagonals in a convex quadrilateral:

{displaystyle p^{2}q^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos {(A+C)}.}

This relationship can be considered as equivalent to the cosine theorem for a quadrilateral. In a cyclic quadrilateral, where A+C=180°, reduces to pq=ac+bd. Since cos(A+C))≥−1, it also provides a proof of Ptolemy's inequality.

Other metric ratios

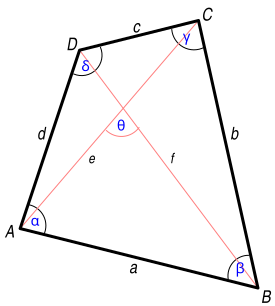
If X and Y are the feet of the normals from B and D to diagonal AC=p in a convex quadrilateral ABCD with sides a=AB, b=BC, c=CD and d=DA, then

{displaystyle XY={frac {|a^{2}+c^{2}-b^{2}-d^{2}|}{2p}}.}

In a convex quadrilateral ABCD with sides a=AB, b=BC, c=CD and d=DA, and where the diagonals intersect at E ,

{displaystyle efgh(a+c+b+d)(a+c-b-d)=(agh+cef+beh+dfg)(agh+cef-beh-dfg)}

where e=AE, f=BE, g=CE, and h=DE.

The shape and size of a convex quadrilateral are completely determined by the lengths of its sequential sides and of a diagonal between two specified vertices. The two diagonals p, q and the four side lengths a, b, c, d of a quadrilateral are related by the Cayley-Menger determinant, as follows:

{displaystyle det {begin{bmatrix}0&a^{2}&p^{2}&d^{2}&1\a^{2}&0&b^{2}&q^{2}&1\p^{2}&b^{2}&0&c^{2}&1\d^{2}&q^{2}&c^{2}&0&1\1&1&1&1&0end{bmatrix}}=0.}

Bisectors

The internal bisectors of a convex quadrilateral form a cyclic quadrilateral (i.e., the four points of intersection of the adjacent bisectors are cocyclic) or are concurrent. In the latter case, it is a circumscribed quadrilateral.

In the quadrilateral ABCD, if the bisectors of A and C coincide with the diagonal BD, then the bisectors of B and D lie on the diagonal AC.

Bimmedian

Main article: Theorem of Varignon

Paralelogram of Varignon (EFGH)

The bimedians of a quadrilateral are the line segments that connect the midpoints of the opposite sides. The intersection of the bimedians is the centroid of the vertices of the quadrilateral.

The midpoints of the sides of any quadrilateral (convex, concave, or crossed) are the vertices of a parallelogram, called a Varignon parallelogram. It has the following properties:

Each pair of opposite sides of the parallelogram of Varignon are parallel to a diagonal in the original quadrilateral.
One side of the parallelogram of Varignon is the half long that the diagonal of the original quadrilateral to which it is parallel.
The area of the parallelogram of Varignon is equal to half of the area of the original quadrilateral. This is true for the convex, concave and cross quadrilateral, provided that the area of the latter is defined as the difference of the areas of the two triangles of which it is composed.
The perimeter of the parallelogram of Varignon is equal to the sum of the diagonals of the original quadrilateral.
Varignon's parallelogram diagonals are the original quadrilateral.

The two bimedians of a quadrilateral and the segment joining the midpoints of the diagonals of that quadrilateral are concurrent, and they are all divided into two equal parts by their point of intersection.

In a convex quadrilateral with sides a, b, c, and d, the length of the bimedian connecting the midpoints of sides a and c is

{displaystyle m={tfrac {1}{2}}{sqrt {-a^{2}+b^{2}-c^{2}+d^{2}+p^{2}+q^{2}}}}

where p and q are the lengths of the diagonals. The length of the bimedian connecting the midpoints of the sides b and d is

{displaystyle n={tfrac {1}{2}}{sqrt {a^{2}-b^{2}+c^{2}-d^{2}+p^{2}+q^{2}}}.}

Therefore,

{displaystyle displaystyle p^{2}+q^{2}=2(m^{2}+n^{2}).}

This is also a corollary to the parallelogram law applied to the Varignon parallelogram.

The lengths of bimedians can also be expressed in terms of two opposite sides and the distance x between the midpoints of the diagonals. This is possible when Euler's quadrilateral theorem is used in the above formulas. then

{displaystyle m={tfrac {1}{2}}{sqrt {2(b^{2}+d^{2})-4x^{2}}}}

and

{displaystyle n={tfrac {1}{2}}{sqrt {2(a^{2}+c^{2})-4x^{2}}}.}

Note that the two opposite sides in these formulas are the two that the bimedian does not connect.

In a convex quadrilateral, there is the following dual connection between the bimedians and the diagonals:

The two bimedians have the same length if and only if the two diagonals are perpendicular to each other.
The two bimedians are perpendicular if and only if the two diagonals have the same length.

Trigonometric identities

The four angles of a simple quadrilateral ABCD satisfy the following identities:

{displaystyle sin {A}+sin {B}+sin {C}+sin {D}=4sin {frac {A+B}{2}}sin {frac {A+C}{2}}sin {frac {A+D}{2}}}

and

{displaystyle {frac {tan {A}tan {B}-tan {C}tan {D}}{tan {A}tan {C}-tan {B}tan {D}}}={frac {tan {(A+C)}}{tan {(A+B)}}}.}

In addition,

{displaystyle {frac {tan {A}+tan {B}+tan {C}+tan {D}}{cot {A}+cot {B}+cot {C}+cot {D}}}=tan {A}tan {B}tan {C}tan {D}.}

In the last two formulas, no angle is allowed to be a right angle, since tan 90° (the trig function tangent to a right angle), is undefined.

Inequalities

Area

If a convex quadrilateral has consecutive sides a, b, c, and d; and the slashes p and q; then its area K satisfies

{displaystyle Kleq {tfrac {1}{4}}(a+c)(b+d)}

(being equality only for a rectangle)

{displaystyle Kleq {tfrac {1}{4}}(a^{2}+b^{2}+c^{2}+d^{2})}

(being equality only for one square)

{displaystyle Kleq {tfrac {1}{4}}(p^{2}+q^{2})}

(being equality only if diagonals are perpendicular and equal)

{displaystyle Kleq {tfrac {1}{2}}{sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}}

(being equality only for a rectangle)

From Bretschneider's formula it follows directly that the area of a quadrilateral satisfies that

{displaystyle Kleq {sqrt {(s-a)(s-b)(s-c)(s-d)}}}

giving equality if and only if the quadrilateral is cyclic or degenerate, in such a way that the length of one side is equal to the sum of the other three (that is, it has collapsed into a segment, so its area is zero).

The area of any quadrilateral also satisfies the inequality

{displaystyle displaystyle Kleq {tfrac {1}{2}}{sqrt[{3}]{(ab+cd)(ac+bd)(ad+bc)}}.}

Denoting the perimeter as L, one has that

{displaystyle Kleq {tfrac {1}{16}}L^{2},}

with equality only in the case of a square.

The area of a convex quadrilateral also satisfies that

{displaystyle Kleq {tfrac {1}{2}}pq}

for lengths of the diagonals p and q, holding equality if and only if the diagonals are perpendicular.

Let a, b, c and d be the lengths of the sides of a convex quadrilateral ABCD with area K and diagonals AC=p and BD=q. then

{displaystyle Kleq {frac {a^{2}+b^{2}+c^{2}+d^{2}+p^{2}+q^{2}+pq-ac-bd}{8}}}

achieving equality only for a square.

Let a, b, c and d be the lengths of the sides of a convex quadrilateral ABCD with area K. Then, the following inequality holds:

{displaystyle Kleq {frac {1}{3+{sqrt {3}}}}(ab+ac+ad+bc+bd+cd)-{frac {1}{2(1+{sqrt {3}})^{2}}}(a^{2}+b^{2}+c^{2}+d^{2})}

achieving equality only for a square.

Diagonals and bimedians

A corollary of Euler's quadrilateral theorem is the inequality

{displaystyle a^{2}+b^{2}+c^{2}+d^{2}geq p^{2}+q^{2}}

where the equality holds if and only if the quadrilateral is a parallelogram.

Euler also generalized Ptolemy's theorem, which is an equality for a cyclic quadrilateral, into an inequality for a convex quadrilateral. He claims that

{displaystyle pqleq ac+bd}

where equality holds if and only if the quadrilateral is cyclic. This relationship is often called the Ptolemaic inequality.

In any convex quadrilateral, the bimedians m and n, and the diagonals p and q are related for inequality

{displaystyle pqleq m^{2}+n^{2},}

holding equality if and only if the diagonals are equal. This follows directly from the identity of the quadrilateral

{displaystyle m^{2}+n^{2}={tfrac {1}{2}}(p^{2}+q^{2}).}

Sides

The sides a, b, c and d of any quadrilateral satisfy that

{frac {d^{2}}{3}}}" xmlns="http://www.w3.org/1998/Math/MathML">a2+b2+c2▪d23{displaystyle a^{2}+b^{2}+c^{2}{2}{frac {d^{2}}{3}}}}{3}}}}{frac {d^{2}}{3}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e84a2737df80480ccad0ceba19d8c45652955000" style="vertical-align: -1.838ex; width:18.285ex; height:5.676ex;"/>

and also

{displaystyle a^{4}+b^{4}+c^{4}geq {frac {d^{4}}{27}}.}

Properties of maximums and minimums

Among all the quadrilaterals with a given perimeter, the one with the largest area is the square. This is called the isoperimetric theorem for quadrilaterals. It is a direct consequence of the inequality of area

{displaystyle Kleq {tfrac {1}{16}}L^{2}}

where K is the area of a convex quadrilateral with perimeter L. The equality holds if and only if the quadrilateral is a square. The Double Theorem states that of all quadrilaterals with a given area, the square has the shortest perimeter. The quadrilateral with given side lengths that has the greatest area is the cyclic quadrilateral. Of all the convex quadrilaterals with given diagonals, the orthodiagonal quadrilateral has the largest area. This is a direct consequence of the fact that the area of a quadrilateral convex satisfies the condition

{displaystyle K={tfrac {1}{2}}pqsin {theta }leq {tfrac {1}{2}}pq,}

where θ is the angle between the diagonals p and q. The equality holds if and only if θ=90°. If P is an interior point in a convex quadrilateral ABCD, then

{displaystyle AP+BP+CP+DPgeq AC+BD.}

From this inequality it follows that the point inside a quadrilateral that minimizes the sum of distances to the vertices is the intersection of the diagonals. Therefore, that point is the Fermat point of a convex quadrilateral.

Notable points and lines in a convex quadrilateral

The center of a quadrilateral can be defined in several different ways. The "centroid of vertices" It comes from considering the quadrilateral as empty but with equal masses at its vertices. The "lateral centroid" comes from considering that the sides have constant mass per unit length. The usual center, called simply the centroid (center of the area), comes from considering that the surface of the quadrilateral has a constant density. In general, these three points are not all the same point. The "centroid of vertices" is the intersection of the two bimedians. As with any polygon, the x and y coordinates of the vertex centroid are the arithmetic mean of the x coordinates i> and y of the vertices. The "centroid of the area" of the quadrilateral ABCD can be constructed as follows. Let G_a, G_b, G_c, G_d the centroids of the triangles BCD, ACD, ABD, ABC respectively. So, the "centroid of the area" is the intersection of lines G_aG_c and G_bG_d.

In a general convex quadrilateral ABCD, there are no natural analogies with the circumcircle and altitude of a triangle. But two of these points can be constructed as follows. Let O_a, O_b, O_c, O_d the circumcenters of the triangles BCD, ACD, ABD, ABC respectively; and let H_a, H_b, H_c and H_d the orthocenters of the same triangles. So, the intersection of the lines O_a O_c and O_b O_d is called the quasicircumcenter, and the intersection of the lines H_aH_c and H _bH_d is called the quasiorthocenter of the convex quadrilateral. These points can be used to define an Euler line of a quadrilateral. In a convex quadrilateral, the quasiorthocenter H, the "centroid of area" G and the quasicircumcenter O are collinear in this order, and HG=2GO. You can also define a 9-point quasicenter E as the intersection of lines E_aE_c and E_bE_d, where E_a, E _b, E_c, E_d are the centers of the nine points of the triangles BCD, ACD, ABD, and ABC respectively. So E is the midpoint of OH. Another notable line in a nonparallelogram convex quadrilateral is Newton's line, which connects the midpoints of the diagonals, the segment connecting these points passes through the centroid of the vertices. A more interesting line (in a sense dual to Newton's line) is the line connecting the point of intersection of the diagonals with the centroid of the vertices. The line is notable for the fact that it contains the centroid (area). The centroid of the vertices divides the segment connecting the intersection of the diagonals and the centroid (area) in the ratio 3:1.

For any quadrilateral ABCD with points P and Q, constructed as the intersections of AD and BC and of AB and CD, respectively, the circles (PAB), (PCD), (QAD), and (QBC) pass through a common point M, called Miquel's point.

Other properties of convex quadrilaterals

Draw the outer squares on all sides of a quadrilateral. The segments that connect the centers of the opposite squares are (a) of equal length, and (b) perpendicular. Thus, these centers are the vertices of an orthodiagonal quadrilateral. This is called Van Aubel's theorem.
For any single quadrilateral with given side lengths, there is a cyclic quadrilateral with the same side lengths.
The four smaller triangles formed by the diagonals and sides of a convex quadrilateral have the property that the product of the areas of two opposite triangles is equal to the product of the areas of the other two triangles.

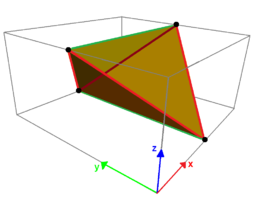
Kinked Quadrilaterals

Contenido relacionado

Más resultados...

Quadrilateral

Elements of a quadrilateral

General propositions

Classification

Nomenclature of quadrilaterals

Simple quadrilaterals

Convex Quadrilaterals

Concave Quadrilaterals

Complex Quadrilaterals

Symmetrical Quadrilaterals

Simple Quadrilaterals

Complex Quadrilaterals

Diverse formulas

Archimedes-Faure theorem

Special segments

Area of a convex quadrilateral

Trigonometric Formulas

Non-Trigonometric Formulas

Vector Formulas

Diagonals

Properties of diagonals in some quadrilaterals

Lengths of diagonals

Generalizations of the Parallelogram Law and Ptolemy's Theorem

Other metric ratios

Bisectors

Bimmedian

Trigonometric identities

Inequalities

Area

Diagonals and bimedians

Sides

Properties of maximums and minimums

Notable points and lines in a convex quadrilateral

Other properties of convex quadrilaterals

Kinked Quadrilaterals

Contenido relacionado

Triangle

Quadratic equation

Twin prime number