Pythagoras theorem

In mathematics, the Pythagorean theorem is a relationship in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the legs (the other two sides that are not the hypotenuse). This theorem can be written as an equation relating the lengths of the sides 'a', 'b' and 'c'. It is the best-known proposition among those that have a proper name in mathematics. The Pythagorean theorem states that, in any right triangle, the length of the hypotenuse is equal to the square root of the sum of the area of the squares of the respective leg lengths.

If in a rectangle triangle there are caetos of length a{displaystyle a,} and b{displaystyle b,}, and the measurement of the hypotenuse is c{displaystyle c,}, then the following relationship is fulfilled:

(1)a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2},}

Three corollaries of algebraic verification and practical application can be deduced from this equation:

a=c2− − b2{displaystyle a={sqrt {c^{2}-b^{2}}}}}

b=c2− − a2{displaystyle b={sqrt {c^{2}-a^{2}}}}}}

c=a2+b2{displaystyle c={sqrt {a^{2}+b^{2}}}}}

The Pythagorean theorem has been proven numerous times by many different methods, possibly the largest number of mathematical theorems. The proofs are diverse, including both geometric and algebraic proofs, some going back thousands of years.

The theorem can be generalized in several ways: to higher-dimensional spaces, to non-Euclidean spaces, to objects that are not right triangles, and to objects that are not triangles at all, but solid n. The Pythagorean theorem has aroused interest outside of mathematics as a symbol of mathematical abstraction, mysticism, or intellectual power; popular references abound in literature, plays, musicals, songs, stamps, and cartoons.

History

The Pythagorean theorem was proven in the VI century BCE. C. by the Greek philosopher and mathematician Pythagoras, but it is estimated that it could have been prior to its existence, or demonstrated under another name.

Regarding the Babylonians there is this note:

From the mathematical point of view, the most important novelties recorded by the Babylonian texts refer to the algebraic solution of linear and quadratic equations, and the knowledge of the so-called "Pythagoras theorem" and its numerical consequences.

There is debate about whether the Pythagorean theorem was discovered once, or many times in many places, and the date of the first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BCE), more than a thousand years before the birth of Pythagoras.

The Pythagorean theorem has this name because its proof, above all, is an effort of the Pythagorean school. Previously, in Mesopotamia and Ancient Egypt, triples of values were known that corresponded to the sides of a right triangle, and they were used to solve problems related to said triangles, as indicated in some tablets and papyri. However, no document that theoretically exposes their relationship has survived. The Pyramid of Khafre, dated to the 26th century BC. C., it was the first great pyramid that was built based on the so-called Egyptian sacred triangle, with proportions 3-4-5.

Conventional designations

Triangles — Overview of Designation Conventions

Vetices	A{displaystyle {text{A}}}	B{displaystyle {text{B}}}	C{displaystyle {text{C}}}
Side (as a segment)	BC{displaystyle {text{BC}}}	AC{displaystyle {text{AC}}}	AB{displaystyle {text{AB}}}
Side (as length)	a{displaystyle a}	b{displaystyle b}	c{displaystyle c}
Angles	α α ^ ^ =a^ ^ =A^ ^ =BAC^ ^ {displaystyle {widehat {alpha}}={widehat {a}}={widehat {a}}}={widehat {BAC}}}}}	β β ^ ^ =b^ ^ =B^ ^ =ABC^ ^ {displaystyle {widehat {beta}}={widehat {b}}={widehat {b}}}{widehat {b}}}{widehat {bb}}}}}}}	γ γ ^ ^ =c^ ^ =C^ ^ =ACB^ ^ {displaystyle {widehat {gamma}}={widehat {c}}={widehat {c}}={widehat {ACB}}}}

Demos

The Pythagorean theorem is one of those with the greatest number of different proofs, using very different methods. One of the reasons for this is that in the Middle Ages a new proof of the theorem was required to achieve the degree of "Magister matheseos".^{[citation required]}

Some authors propose up to more than a thousand demos. For example, the American mathematician E. S. Loomis cataloged 367 different proofs in his 1927 book The Pythagorean Proposition.^{[citation needed]}

Graphical Demonstration of the Theorem of Pythagoras- School workshop.

In that same book, Loomis would classify proofs into four large groups: algebraic, where the sides and segments of the triangle are related; the geometric ones, in which comparisons of areas are made; dynamics, through the properties of force, mass, and quaternionics, through the use of vectors.^{[citation needed]}

China: Zhoubi Suanjing and Jiuzhang Suanshu

Visual proof for a triangle a= 3, b= 4 and c= 5 as seen in Chou Pei Suan Ching, 500-200 a. C.

The Zhoubi Suanjing is a mathematical dating work disputed in some places, although it is widely accepted that it was written between 500 and 300 BC. C. It is believed that Pythagoras did not know this work. As for the Jiuzhang Suanshu, it seems to be later; It is dated around the year 250 B.C. c.

The Zhou Bi proves the theorem by constructing a square with side (a+b) that is divided into four triangles with base a and height b, and a square with side c.

Demonstration

Let be the right triangle with legs a and b and hypotenuse c. It is about proving that the area of the square of side c is equal to the sum of the areas of the squares of side a and side b. That is to say:

a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2},}

If we add three triangles equal to the original inside the square with side c forming the figure shown in the image, we obtain a smaller square. It can be seen that the resulting square does indeed have a side of b - a. Then, the area of this smaller square can be expressed as follows:

(a− − b)2=a2− − 2ab+b2{displaystyle (a-b)^{2}=a^{2}-2ab+b^{2},}

Since (b− − a)2=(a− − b)2{displaystyle (b-a)^{2}=(a-b)^{2},}.

It is evident that the area of the square of side c is the sum of the area of the four triangles of height a and base b that are inside it plus the area of the smaller square:

c2=4⋅ ⋅ (a⋅ ⋅ b2)+a2− − 2ab+b2=a2+b2{displaystyle c^{2}=4cdot left({frac {acdot b}{2}{2}{2}{2}-2ab+b^{2}=a^{2} +b^{2}}}

With which the theorem is proved.

Supposed proofs of Pythagoras

It is estimated that the theorem was proved by similar triangles: their homologous sides are proportional.

Let the triangle ABC be a right triangle at C. The segment CH is the altitude relative to the hypotenuse, in which it determines the segments a' and b', projections in it of the legs a and b, respectively.

Right triangles ABC, AHC and BHC have their three bases equal: they all have two bases in common, and the acute angles are equal either because they are common or because they have perpendicular sides. Consequently, these triangles are similar.

• From the similarity between ABC and AHC:

and two triangles are similar if there are two or more congruent angles.

bb♫=cb{displaystyle {frac {b}{b}}}{frac {c}{b}}}}}

b2=b♫c{displaystyle b^{2} = b'c}

• From the similarity between ABC and BHC:

aa♫=ca{displaystyle {frac {a}{a}{a'}}{frac {c}{a}{a}}}}}}}

a2=a♫c{displaystyle a^{2} = a'c}

The results obtained are the leg theorem.

Summing:

a2+b2=a♫c+b♫c=c(a♫+b♫){displaystyle a^{2} + b^{2}=a'c + b'c = cleft(a'+b'right)}

But (a♫+b♫)=c{displaystyle left(a'+b'right)=c}, so it finally turns out:

a2+b2=c2{displaystyle a^{2} + b^{2}=c^{2}}

Pythagoras could also have proved the theorem based on the relationship between the surfaces of similar figures.

Triangles PQR and PST are similar, so:

ru=sv=r{displaystyle {frac {r}{u}}}={frac {s}{v}=r}

where r is the ratio of similarity between said triangles. If we now look for the relationship between their surfaces:

SPQR=12(rs){displaystyle S_{PQR} = {frac {1}{2}}left(rsright}

SPST=12(uv){displaystyle S_{PST} = {frac {1}{2}}left(uvright)}

we obtain after simplifying that:

SPQRSPST=rsuv=ru⋅ ⋅ sv{displaystyle {frac {S_{PQR}}{S_{PST}}}}={frac {s}{uv}}}={frac {r}{u}}}}cdot {frac {s}{v}}}}}}}

but being ru=sv=r{displaystyle {frac {r}{u}}}={frac {s}{v}=r} the reason for likeness, it is clear that:

SPQRSPST=(ru)2=(sv)2{displaystyle {frac {S_{PQR}}{S_{PST}}}}}=left({frac {r}{u}}}{2}{2}=left({frac {s}{v}}}right)^{2}

That is, "the ratio between the surfaces of two similar figures is equal to the square of the ratio of similarity".

Applying this principle to the similar right triangles ACH and BCH we have:

SACHSBCH=(ba)2{displaystyle {frac {S_{ACH}}{S_{BCH}}}}}=left({frac {b}{a}{a}}{right)^{2}}}

which according to the properties of proportions gives:

SACHb2=SBCHa2=SACH+SBCHb2+a2{displaystyle {frac {S_{ACH}}{b^{2}}}}{{frac {S_{BCH}}{a^{2}}}}}{frac {S_{ACH}}}}{b^{2}+a^{2}}}}}}}} (I)

and by the similarity between the triangles ACH and ABC it turns out that:

SACHSABC=(bc)2{displaystyle {frac {S_{ACH}}{S_{ABC}}}}}=left({frac {b}{c}{c}}right)^{2}}}

SACHb2=SABCc2{displaystyle {frac {S_{ACH}}{b^{2}}}}}{{frac {S_{ABC}}{c^{2}}}}}}}}}

but according to (I) SACHb2=SACH+SBCHb2+a2{displaystyle {frac {S_{ACH}}{b^{2}}}}{{frac {S_{ACH+S_{BCH}}}{b^{2}+a^{2}}}}}}}}}}So...

SACH+SBCHb2+a2=SABCc2{displaystyle {frac {S_{ACH}+S_{BCH}}{b^{2+}a^{2}}}}{frac {S_{ABC}}{c^{2}}}}}}}}{

and therefore:

b2+a2=c2{displaystyle b^{2} + a^{2} =c^{2}}

proving the Pythagorean theorem.

It is also possible that Pythagoras had obtained a graphical proof of the theorem.

Starting with the initial configuration, with the right triangle with sides a, b, c, and the squares corresponding to the legs and hypotenuse -left-, two different squares are constructed:

• One of them – center– is formed by the squares of the caetos, plus four rectangles triangles equal to the initial triangle.
• The other square – right – is made up of the same four triangles, and the square of the hypotenuse.

If each of these squares are removed from the triangles, obviously the gray square area (c2{displaystyle c^{2}}) equals that of the yellow and blue squares (b2+a2{displaystyle b^{2}+a^{2}}), having been shown the theorem of Pythagoras.

Euclid's proof: proposition I.47 of The Elements

The discovery of irrational numbers by Pythagoras and the Pythagoreans was a very serious setback. Suddenly, the proportions were no longer universally valid, they could not always be applied. Pythagoras' proof of his theorem was most likely based on proportions, and a proportion is a rational number. Would it really be valid as a demo? Given this, Euclid elaborates a new demonstration that avoids the possibility of encountering irrational numbers.

The axis of his proof is proposition I.47 of The Elements:

Based on proposition I.41 of The Elements, which is equivalent to saying that with the same base and height, the area of the parallelogram doubles that of the triangle, (see Figure Euclid 1).

There is triangle ABC, right-angled at C (see Figure Euclid 3), and the squares corresponding to legs and hypotenuse are constructed. The height CH is extended to J. Next, four triangles are drawn, equal two by two:

• Triangles ACK and ABD: are the same, since the AD and AC sides are the same and perpendicular; and being AB and AK also equal and forming the same angle as AD and AC, necessarily the DAB angle is equal to the CAK angle, so BD=KC. Its three sides are the same.
• ABG and CBI triangles: analogously, BA=BI, and BG=BC, so AG=IC. Its three sides are also equal.

Alonging on the above considerations, note that a turn centered on A, and in a positive direction, transforms ABD into ACK. And a turn centered on B, and also in a positive direction, transforms ABG into CBI. In Leonardo da Vinci's proof you will again come across twists that prove the equality of figures.

See (in Figure Euclid 3) that:

1. The parallels r and s comprise the triangle ACK and the rectangle AHJK, which have the same base, AK. Therefore according to proposition I.41 of The Elements, AHJK has double area that ACK, (see Figure Euclides 1).
2. The parallels m and n contain ABD and ADEC, whose common base is AD. So the ADEC area is double that of ABD.

But being ACK=ABD, it turns out that the rectangle AHJK and the square ADEC have equivalent areas. Making similar reasonings with the triangles ABG and CBI, with respect to the square BCFG and the rectangle HBIJ respectively, it is concluded that the latter also have equal areas. From the above, it immediately follows that: "the sum of the areas of the squares built on the legs is equal to the area of the square built on the hypotenuse."

Pappus demo

About 625 years after Euclides, Pappus seems to follow his path, and develops a demonstration of the Pythagorean theorem based on I.36 proposition The Elements of Euclides:

Two parallels are of equal base, and between the same parallels, have equivalent surfaces.

We start from the right triangle ABC in C, on whose legs and hypotenuse we have built the corresponding squares.

Prolonging CH upwards obtains the rectangle CEGI whose diagonal CG determines in that two right triangles equal to the given triangle ABC:

• Acute angles GCI and ABC have their perpendicular sides
• The CI side is equal to the CB side

Consequently, the right triangles ABC, ICG and EGC have three equal sides.

1. The parallels are ACGF and AHMN have the same CG=HM base, and are included in the same parallels, r and s. Therefore they have the same surface (Elements I.36)
2. Applying the same principle to ACGF and ACED – common ground AC, and parallel m and n– it turns out that both parallels have similar surfaces.

From 1) and 2) it follows that the surfaces of ACED and AHMN are equal.

Similarly:

1. CGJB and BLMH have the same CG=MH base, and are included in the parallels s and t. Its surfaces are equivalent.
2. CGJB and CIKB have common base CB, and are among the parallels or and p. Its surfaces are equal.

From where the equivalence of the surfaces of BLMH and CIKB can be deduced.

The Pythagorean theorem is proven.

Bhaskara Demo

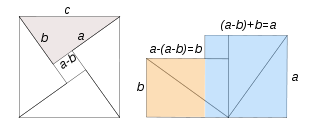Bhaskara II, the Hindu mathematician and astronomer of the centuryXII, gave the following demonstration of the theorem of Pythagoras.

With four right triangles with sides a, b and c, the square with side c is built –left-, in the center of which another square with sides (a-b) is formed.

Redistributing the four triangles and the square on each side (a-b), we build the figure on the right, whose surface turns out to be the sum of the two squares: one with side a -blue- and another with side b -orange-.

It has been shown graphically that c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2}}

Algebraically: the area of the square with side c is that corresponding to the four triangles, plus the area of the central square with side (a-b), that is:

c2=4⋅ ⋅ ab2+(a− − b)2{displaystyle c^{2}=4cdot {frac {ab}{2}}{2}}{2}}{2}}

developed and simplified expression gives us the result c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2}}and theorem is proved.

Leonardo Da Vinci Demonstration

The genius of the Renaissance, Leonardo da Vinci, is not missing from the list of intelligences that addressed the Pythagorean theorem.

Starting with the right triangle ABC with the squares of the legs and the hypotenuse, Leonardo adds the triangles ECF and HIJ, equal to the given one, resulting in two polygons, whose surfaces are going to be shown to be equivalent:

1. ADEFGB polygon: the DG line divides it into two identical halves, ADGB and DEFG.
2. Polygon ACBHIJ: the CI line determines CBHI and CIJA.

Let's compare the polygons highlighted in gray, ADGB and CIJA:

• We immediately see that they have three equal sides: AD=AC, AB=AJ, BG=BC=IJ
• Equality between the angles of the following vertices is also immediate:
  • A by ADGB and A by CIJA
  • B of ADGB and J of CIJA

It is concluded that ADGB and CIJA are the same.

Similarly, the equality between ADGB and CBHI is checked.

In addition, in a similar way to what was explained in Euclid's proof, note that a rotation of center A, and positive sense, transforms CIJA into ADGB. While a turn of center B, and negative direction, transforms CBHI into ADGB.

All of this leads us to the fact that the polygons ADEFGB and ACBHIJ have equivalent areas. Well then, if we remove their two triangles from each one –equal– the remaining surfaces will necessarily be equal. And these surfaces are nothing but the two squares of the legs in the polygon ADEFGB, on the one hand, and the square of the hypotenuse in the polygon ACBHIJ, on the other. The Pythagorean theorem is proven.

Garfield Demonstration

James Abram Garfield (1831-1881), the 20th President of the United States, developed a demonstration of the theorem of Pythagoras published in the New England Journal of Education.

Garfield constructs a trapezoid with bases a and b, and height (a+b), from the right triangle with sides a, b, and c. Said trapezoid is made up of three right triangles: two equal to the given one, and a third, isosceles with legs c. Consequently:

(g.1)Srag=a+b2⋅ ⋅ (a+b){displaystyle S_{text{trapecio}}}={frac {a+b}{2}cdot (a+b)}

as corresponds to the surface of the trapezoid, but we also have a figure composed of three triangles, two of them equal, so that:

(g.2)S=2⋅ ⋅ ab2+c22{displaystyle S=2cdot {frac {ab}{2}}} +{frac {c^{2}}{2}}}}}

equating the equation (g.2) with the ( g.1) we get:

(ab)+c22=12(a+b)⋅ ⋅ (a+b){displaystyle (ab)+{frac {c^{2}}{2}}}={frac {1}{2}{2}(a+b)cdot (a+b)}}}}

multiplying both sides by 2{displaystyle 2} and simplifying...

2ab+c2=(a+b)2{displaystyle 2ab+c^{2}=(a+b)^{2},}

expanding the right member...

2ab+c2=a2+2ab+b2{displaystyle 2ab+c^{2}=a^{2}+2ab+b^{2},}

subtract 2ab{displaystyle 2ab} to both members, finally gives us:

c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2},}

and the theorem is proven.

Test using a geoboard

It is possible, rather than a generic demonstration, to verify the correctness of the proposition using a geoboard, only for special and specific cases, previously known.

Converse of the Pythagorean Theorem

If in an ABC triangle, being the main side a is fulfilled a2=b2+c2{displaystyle a^{2}=b^{2}+c^{2}}} Then the triangle is rectangle.

Uses of the theorem in mathematics

Pythagorean triples

A Pythagorean triple has three positive integers a, b and c, such that a² + b² = c².. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle in which all three sides have integer lengths. This triple is often written (a, b, c). Some familiar examples are (3, 4, 5) and (5, 12, 13).

A primitive Pythagorean triple is one in which a, b and c are coprime, that is, that the greatest common divisor of a, b and c is 1.

The following is a list of primitive Pythagorean triples with values less than 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Converse Pythagorean Theorem

Given a rectangle triangle with sides a,b,c{displaystyle a,b,c} and altitude d{displaystyle d} (a straight angle and perpendicular to the hypotenuse c{displaystyle c}). The theorem of Pythagoras has,

a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2}}

while the Reciprocal Pythagorean Theorem or Pythagoras theorem backwards relates the two caetos a,b{displaystyle a,b} with the altitude d{displaystyle d},

1a2+1b2=1d2{displaystyle {frac {1}{a^{2}}}} +{frac {1{b^{2}}}}}}{{frac {1}{d^{2}}}}}}}}}}}}

The equation can be transformed into, 1(xz)2+1(andz)2=1(xand)2{displaystyle {frac {1}{(xz)^{2}}}}} +{frac {1}{(yz)^{2}}}}{frac {1}{(xy)}{2}}}}}}}}}where x2+and2=z2{displaystyle x^{2}+y^{2}=z^{2}}} for any real no null x,and,z{displaystyle x,y,z}. Yeah. a,b,d{displaystyle a,b,d} must be integer, the smallest solution b>d}" xmlns="http://www.w3.org/1998/Math/MathML">a▪b▪d{displaystyle a rigidity}b>d}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/70b187df67277382b0c16e506317db210e2b4f7d" style="vertical-align: -0.338ex; width:9.64ex; height:2.176ex;"/> It's then. 1202+1152=1122{displaystyle {frac {1}{20^{2}}}} +{frac {1{15^{2}}}}}}{frac {1}{12^{2}}}}}}}}}}}}}using the smallest triple pythagorean 3,4,5{displaystyle 3.4,5}. Reciprocal Pythagorean Theorem is a special case of optical equation

1p+1q=1r{displaystyle {frac {1}{p}}}+{frac {1}{q}}}{frac {1}{1}{r}}}}}}

where denominators are square and also for a heptagonal triangle whose sides p,q,r{displaystyle p,q,r} It's square numbers.

The Pythagoreans

One of the best-known legacies of Pythagoreanism, to mathematics, is the hypotenuse theorem, better known as the Pythagorean Theorem. It is not clearly established whether this was the work of the Master or his disciples, since the Pythagoreans were great mathematicians who used to attribute all his discoveries to Pythagoras (

Other usage examples

• To calculate the length e of a staircase; the height is known h from the wall to reach; the distance p from the line floor wall to the foot of the stairs. The equation is fulfilled e2=h2+p2{displaystyle e^{2}=h^{2}+p^{2}}the value of e is cleared by e=h2+p2.{displaystyle e={sqrt {h^{2}+p^{2}}}}}. !

• In flat analytical geometry, to find the distance between the points C(x1,and1),D(x2,and2){displaystyle C(x_{1},y_{1}),D(x_{2},y_{2}}}}} equality CD2=(x2− − x1)2+(and2− − and1)2.{displaystyle CD^{2}=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}. !

• In trigonometry to demonstrate the fundamental identity sen2 α α +#2 α α =1{displaystyle operatorname {sen} ^{2}alpha +cos ^{2}alpha =1}between the breast and the cosine.
• In geometry to calculate the height of an equilateral triangle depending on the side; to obtain the height of the regular tetraedro using the edge. To find the apothesis of an equilateral triangle and a regular hexagon registered, knowing the radius of the circumscribed circumference.

• In algebraic number theory to analyze if a whole Gaussian is a Gaussian cousin. For example α α =1+4i{displaystyle alpha =1+4i}whose rule is N(α α )=12+42=17.{displaystyle N(alpha)=1^{2}+4^{2}=17. !