Projective module

In mathematics, particularly abstract algebra and homological algebra, the concept of a projective modulus over a ring R is a looser generalization of the idea of a free modulus (i.e., a modulus with vectors base). There are several equivalent characterizations of these modules.

Definitions

Direct addends of free modules

Easiest characterization is as direct addition of a free module. That is, a module P is projective when there is a module Q such that the direct sum of the two is a free module F. From this it follows that we can think of P as a kind of projection on F: the endomorphism of modules on F which is the identity in P and 0 in Q is an idempotent matrix.

Elevation Property

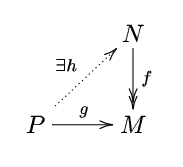
Another way that is more in line with category theory is to extract the lift property that transports from free to projective modules. Using a basis of a free module F, it is easy to see that if we are given a surjective homomorphism from module N to M, the corresponding function from Hom(F, N) to Hom(F, M) is also surjective (is of a product of copies of N to a product with the same indices for M). Using the homomorphisms P → F and F → P for a projective module, it is easy to see that P has the same property; and also if we can raise the identity P → P to P → F for F some free module mapped onto P, P is a direct addend.

We can summarize this lifting property as follows: a module P is projective if and only if for any homomorphism of surjective modules f: N → M and every homomorphism of modules g: P → M, there exists a homomorphism h: P → N such that fh = g. (We do not require that the elevation homomorphism h be unique; this is not a universal property.)

The advantage of this definition of "projective" is that it can be realized in more general categories than module categories: we don't need a notion of "free object". It can also be dualized, leading to injective modules.

For modules, the lift property can be equivalently expressed as follows: the module P is projective if and only if for every surjective module homomorphism f: M → P there exists a homomorphism of modules h: P → M such that fh = identity_P. The existence of such a section h implies that P is a direct addend of M and that f is essentially a projection in the addend P.

Vector bundles and locally free modules

A basic motivation of the theory is that projective modules (at least over certain commutative rings) are analogous to vector bundles. This can be made accurate for the ring of continuous real-valued functions on a compact Hausdorff space, as well as for the ring of differentiable functions on a compact differentiable manifold (see Swan's theorem).

Vector bundles are locally free. If there is a certain notion of "location" that can be transported to the modules, for example that given in the location of a ring, locally free modules can be defined, and the projective modules then typically coincide with the locally free ones. Specifically, a finitely generated module on a commutative ring is locally free if and only if it is projective.

Facts

Direct sums and direct addends of projective modules are projective.

If e = e² is an idempotent in the ring R, then Re is a left module projective onto R.

Submodules of projective modules do not have to be projective.

Each module on a body or oblique body is projective (even free). A ring about which each module is projective is called semisimple.

An abelian group (ie a module on Z) is projective if it is a free abelian group. Same all main domains; the reason is that for these rings, any submodule of a free module is free.

Each projective module is flat. The converse is not, in general, true: Q is a planar abelian group that is not projective.

In line with the above intuition of "locally free = projective" There is the following theorem, due to Kaplansky: on a local ring R, each projective module is free. This is easy to prove for finitely generated projective modules, but the general case is difficult.

The Quillen-Suslin theorem is another profound result; states that if K is a field and R = K then [X₁..., X_n] is a ring of polynomials over K, then each projective module over R is free.