Program review and evaluation technique

ImprimirCitar

PERT network diagram for a seven-month project with 6 activities (A to F) and 5 nodes

The Technique of Review and Evaluation of Programs (or Projects) (from English PERT, Program Evaluation and Review Techniques) is a statistical technique of administration and project management that was designed to analyze and represent the tasks involved in completing a project.

Developed in 1957 by the US Department of Defense Office of Special Projects Navy as part of the Polaris submarine-launched mobile ballistic missile project. This project was a direct response to the Sputnik crisis.

Description

PERT is basically a method of analyzing the tasks involved in completing a given project, especially the time to complete each task, and identifying the minimum time needed to complete the total project.^{[citation needed]}

It is an algorithm designed for efficient project planning, from the beginning to the end, the result of the application of this algorithm is a task schedule, which determines the total duration of the project and the classification of tasks according to priority.

This project model was the first of its kind, and provided a new impetus for scientific management, founded by Fordism and Taylorism. Other types of project models are not very common, virtually all of them are based on PERT in some way. Just the DuPont Corporation's critical path method (CPM) which was invented around the same time as PERT.

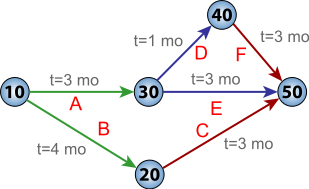
The most famous part of PERT is the PERT Networks, diagrams of interconnecting time lines.

PERT Networks

A PERT mesh allows planning and controlling the development of a project. Unlike CPM networks, PERT networks work with probabilistic times.

Normally, to develop a specific project, the first thing that is done is to determine, in a multidisciplinary meeting, what are the activities that must be executed to complete the project according to the established requirements, what is the precedence between them and what will be the expected duration of each one.

To define the precedence between activities, a certain amount of professional experience is required in the area, in related projects.

Principles

These three principles must always be respected when drawing a PERT mesh:

Successive designation principle: the vertices are named according to the natural numbers, so that they are not assigned number until they have been appointed all those of those who leave edges that will stop them.

Principle of uniqueness of the initial and final state: the existence of more than one initial or final vertex is prohibited. There is only one start-up and one end-of-the-project situation.

Unique designation principle: There can be no two edges that have the same nodes of origin and destiny. Normally, activities are named through the pair of vertices that unite. If this principle is not respected, two edges may receive the same denomination.

Duration of an Activity

To estimate the expected duration of each activity it is also desirable to have previous experience in carrying out similar tasks. In project planning and scheduling, it is estimated that the expected duration of an activity is a random variable of probability distribution Beta unimodal of parameters (o, m, p) where:

${displaystyle t_{o}}$ = It is defined as the optimistic time at the least time that an activity can last.

$t_{m}$ = It is the most likely time that an activity could last.

${displaystyle t_{p}}$ = This is the pessimistic time, or the longer a activity can last.

$t_{e}$ = Correspond to expected time for an activity (This corresponds to the time CPM, assuming that the calculations are accurate).

NOTE: Each Task is supposed to follow a law of distribution $B$ from Euler.

The expected value (or time) in this distribution. This is expressed in the following formula:

{displaystyle t_{e}={frac {t_{o}+4t_{m}+t_{p}}{6}}}

whose variance is given by:

{displaystyle sigma ^{2}=left({frac {t_{p}-t_{o}}{6}}right)^{2}}

and a standard deviation:

{displaystyle sigma ={frac {t_{p}-t_{o}}{6}}}

Drawing a PERT mesh

There are two accepted methodologies to draw a PERT mesh, that of "Activity in the Arc" and those of "Activity in the Node", the latter being the most widely used at present because it is the one used by the majority of the computer applications specialized in this topic.

In a drawing of a PERT mesh we can distinguish nodes and arcs, the nodes represent instants in time. Specifically, they represent the start time of one or several activities and simultaneously the end time of several other activities. The arcs for their part represent the activities, they have an initial node and a termination node where it reaches the arrowhead. Associated with each arc is the expected duration of the activity. More information from an activity diagram is to represent these with a complexity rating to minimize the bottleneck effect.

Red PERT.

Each node contains the following information about the activity:

Name of activity;
Expected duration of activity (t);
Early start time (ES = Earliest Start);
Earlier term time (EF = Earliest Finish);

Another way to represent the PERT network
Late start time (LS = Latest Start);
Late term time (LF = Latest Finish);
Holgura of Activity (H);

By convention, arcs are always drawn oriented to the right, towards the termination node of the project, never going backwards. The drawing of a PERT mesh is started at the start node of the project. From it, the activities that do not have preceding activities are drawn, that is, those that do not have to wait for other activities to finish before they can start. Next, the remaining activities are drawn, taking care to respect the precedence between them. At the end of the drawing of the preliminary mesh, there will be several blind nodes, terminal nodes that are reached by those activities that are not predecessors of any other, that is, those that do not influence the start date of any other, these are the terminal activities and therefore attend the end node of the project.

Calculating the earliest start and finish times

The earliest start time “ES” (Early Start) and earliest completion time “EF” (Early finish) for each project activity are calculated from the start node to the project completion node according to the following relationship: The expected duration of the project (T) is equal to the greatest of the EF times of all the activities that lead to the completion or completion node of the project.

Calculation of latest start and finish times

The latest start time “LS” (Latest Start) and latest finish time “LF” (Latest finish) for each project activity are calculated from the finish node back to the project start node according to the following relationship:

LS = LF - t

Where (t) is the expected duration of the activity and where LF is defined according to the following rule:

Rule of the most late completion time:

The most late completion time, LF, of a specific activity, is equal to the lesser of the LS times of all activities that begin exactly after it.

The most late completion time of the activities ending in the project completion node is equal to the expected duration of the project (T).

Slack, Critical Activities, and Critical Paths

The Slack of an activity is the time that is available to either delay its start date, or lengthen its expected execution time, without this causing any delay in the project completion date.

The slack of an activity is calculated as follows:

H = LF - EF

H = LS - ES

Critical activities

It is called critical activities to those activities whose slackness is null and therefore, if they are delayed at their start date or longer in their execution beyond their expected duration, they will cause a delay exactly the same in time at the end date of the project.

Critical routes

It is called critical routes to the continuous paths between the start node and the project completion node, whose component arches are all critical activities.

Critical routes are named by the sequence of critical activities that make up it or by the sequence of nodes through which it passes.

Note that a project may have more than one critical route but at least you will always have one.

Total Holgura

The total soothing is the interval during which an operation, which starts from the earliest dates, can be moved to the future without affecting the later dates of the successor operations or the extreme end date of the graph. The total sooth may be less than, greater than or equal to zero (total fat = later end - sooner term). If the earliest and later dates of an operation coincide on the same day, the total soot will be zero. The operations with the minor total soot are called "critical". The critical path is the path through the graph in which operations and their management relationships are ordered so that the total slackness is minimal. Generally, the critical path is the longest time needed to produce the graph.

Free Holgura

The free soothe is the interval during which an operation, which starts from the earliest dates, can move to the future without affecting the earliest dates of the successive operations or the extreme end date of the graph. Free soothe can't be less than zero or greater than total soothe. The system first calculates the earliest start date for all successor operations and detracts the range of the management relationship. The smaller date less the earliest start date of an operation determines the free.g ra soot assuming that the expected duration of an activity is an independent random variable, we can also assume that the expected duration of the project is a random variable that approximates the distribution of Gauss (for tasks  30) and therefore we can calculate some odds using a normal distribution table, taking into consideration the following relationships:

- Consider that for Task Numbers ≤30, you should approach a Student Distribution:

P=JI-1-i

The probability that the project will be completed before a given duration t0 is given by:

<math alttext="{displaystyle Pleft{T<=t_{0}right}=Pleft{ZP{T♫t0!=P{Z♫z0!{displaystyle Pleft{T margin=t_{0}right}=Pleft{Z con=z_{0}right}}}<img alt="P left { T <= t_{0} right } = Pleft { Z

where

z_{0}

is the input value to a normal distribution table and is calculated as follows:

z_{0} = frac{t_{0} - T}{sigma_{T}}

Contenido relacionado

Más resultados...