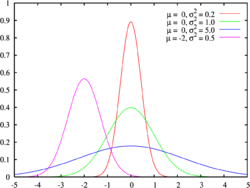
Probability density function

Box diagram and probability density function of a normal distribution N(0,σ²).

In probability theory, the probability density function, density function, or simply density of a continuous random variable describes the relative probability that the random variable will take on a certain value.
The probability that the random variable falls in a specific region of the possibility space will be given by the integral of the density of this variable between one and the other limit of said region.
The probability density function (PDF) is positive throughout its entire domain and its integral over the entire space is of value unitary.

Definition

A probability density function characterizes the probable behavior of a population as it specifies the relative possibility that a continuous random variable X{displaystyle X} take a value close to x{displaystyle x}.

A random variable X{displaystyle X} has density function fX{displaystyle f_{X}}, being fX{displaystyle f_{X}} a non-negative integrated function of Lebesgue, yes:

P [chuckles]a≤ ≤ X≤ ≤ b]=∫ ∫ abfX(x)dx{displaystyle operatorname {P} [aleq Xleq b]=int _{a}{b}f_{X}(x),dx}

Yeah. FX{displaystyle F_{X}} is the distribution function X{displaystyle X}, then

FX(x)=∫ ∫ − − ∞ ∞ xfX(u)du{displaystyle F_{X}(x)=int _{-infty }^{xf}{X}(u),du}

and (yes) fX{displaystyle f_{X}} is continuous x{displaystyle x})

fX(x)=ddxFX(x){displaystyle f_{X}(x)={frac {d}{dx}}F_{X}(x}

Intuitively, it can be considered fX(x)dx{displaystyle f_{X}(x)dx} like the probability of X{displaystyle X} of fall in the infinitesimal interval [chuckles]x,x+dx]{displaystyle [x,x+dx]}.

Formal definition

The formal definition of the density function requires concepts from measurement theory.

A continuous random variable X{displaystyle X} with values in a measurable space (X,A){displaystyle ({mathcal {X}},{mathcal {A}}}} (usually Rn{displaystyle mathbb {R} ^{n} with Borel assemblies as measurable subsets), has as probability distribution the measurement X_↓P in (X,A){displaystyle ({mathcal {X}},{mathcal {A}}}}: the density of X{displaystyle X} with respect to the reference measure μ μ {displaystyle mu } on (X,A){displaystyle ({mathcal {X}},{mathcal {A}}}} is the derivative of Radon-Nikodym.

f=dX↓ ↓ Pdμ μ .{displaystyle f={frac {dX_{*}P}{dmu }}}. !

This is, f{displaystyle f} is a measurable function with the following property:

P [chuckles]X한 한 A]=∫ ∫ X− − 1AdP=∫ ∫ Afdμ μ {displaystyle operatorname {P} [Xin A]=int _{X^{1A},dP=int _{A}f,dmu }

for all measurable set A한 한 A{displaystyle Ain {mathcal {A}}}.

Properties

From the properties of the density function follow the following properties of the nfd (sometimes seen as pdf):

• fX(x)≥ ≥ 0{displaystyle f_{X}(x)geq 0} for all x{displaystyle x}.
• The total area enclosed under the curve is equal to 1:

∫ ∫ − − ∞ ∞ ∞ ∞ fX(x)dx=1{displaystyle int _{-infty }^{infty }f_{X}(x),dx=1}

• The probability that X{displaystyle X} take a value in the interval [chuckles]a,b]{displaystyle [a,b]} is the area under the curve of the density function in that interval or what is the same, the integral defined in that interval. The chart f(x) is sometimes known as density curve.

P [chuckles]a≤ ≤ X≤ ≤ b]=∫ ∫ abfX(x)dx=F(b)− − F(a){displaystyle operatorname {P} [aleq Xleq b]=int _{a}{b}f_{X}(x),dx=F(b)-F(a)}}

Some FDPs are declared in ranks of − − ∞ ∞ {displaystyle -infty ;} a +∞ ∞ {displaystyle +infty ;}Like normal distribution.

Densities associated with multiple variables

For continuous random variables X1,X2,...... ,Xn{displaystyle X_{1},X_{2},dotsX_{n}} It is possible to define a function of probability of density, this is called joint density function. Joint density function is defined as a function of n{displaystyle n} variables, such that for any domain D{displaystyle D} in space n{displaystyle n}- dimensional of the values of the variables X1,X2,...... ,Xn{displaystyle X_{1},X_{2},dotsX_{n}}, the probability of occurrence of a set of variables is found within D{displaystyle D} That's it.

P [chuckles]X1,...... ,Xn한 한 D]=∫ ∫ ∫ ∫ DfX1,...... ,Xn(x1,...... ,xn)dx1 dxn{displaystyle operatorname {P} [X_{1},dotsX_{n}{nin D]=int cdots int _{D}f_{X_{1},dotsX_{n}}}(x_{1},dotsx_{n}};dx_{1cdots dx_{n}{n}

Yeah. F(x1,...... ,xn)=P [chuckles]X1≤ ≤ x1,...... ,Xn≤ ≤ xn]{displaystyle F(x_{1},dotsx_{n})=operatorname {P} [X_{1}{1},dotsX_{n}leq x_{n}}}}}}} is the vector distribution function (X1,X2,...... ,Xn){displaystyle (X_{1},X_{2},dotsX_{n})} then the joint density function can be obtained as a partial derivative

f(x1,...... ,xn)=▪ ▪ F▪ ▪ x1 ▪ ▪ xn{displaystyle f(x_{1},dotsx_{n})={frac {partial F}{partial x_{1}cdots partial x_{n}}}}}}}}}}}

Marginal density

Stop. i=1,...... ,n{displaystyle i=1,dotsn} Whatever. fXi(xi){displaystyle f_{X_{i}}(x_{i})} the density function associated with the variable Xi{displaystyle X_{i}}, this function is called marginal density function and can be obtained from the joint density function associated with the variables X1,X2,...... ,Xn{displaystyle X_{1},X_{2},dotsX_{n}} Like

fXi(xi)=∫ ∫ ∫ ∫ n− − 1fX1,...... ,Xn(x1,...... ,xn)dx1 dxi− − 1dxi+1 dxn{displaystyle f_{X_{i}}(x_{i})=underbrace {int cdots int } _{n-1}f_{X_{1},dotsX_{n}{n}}(x_{1},dotsx_{n}, dx_{1}{1⁄cdots}{i_{ix1⁄2}{i1⁄2}

Sum of independent random variables

The density function of the sum of two independent random variables U{displaystyle U} and V{displaystyle V}, each with density function, is the convolution of its density functions:

fU+V(x)=∫ ∫ − − ∞ ∞ ∞ ∞ fU(and)fV(x− − and)dand=(fU↓ ↓ fV)(x){displaystyle f_{U+V}(x)=int _{-infty }^{infty} {Uf_{U}(y)f_{V}(x-y);dy=(f_{U}*f_{V})(x)}

It is possible to generalize the result prior to the sum of N{displaystyle N} independent random variables with density U1,...... ,UN{displaystyle U_{1},dotsU_{N}}}

fU1+ +UN(x)=(fU1↓ ↓ ↓ ↓ fUN)(x){displaystyle f_{U_{1}+cdots +U_{N}}}(x)=(f_{U_{1}}}*cdots *f_{U_{N}}})(x)}

Example

Suppose bacteria of a certain species normally live for 4 to 6 hours. The probability that a bacterium lives exactly 5 hours is equal to zero. Many bacteria live for about 5 hours, but there is no probability that a given bacterium will die at exactly 5:00... hours. However, the probability that the bacteria will die between 5 hours and 5.01 hours is quantifiable. Suppose the answer is 0.02 (ie 2%). So, the probability that the bacterium will die between 5 hours and 5,001 hours should be about 0.002, since this time interval is one-tenth of the previous one. The probability that the bacteria will die between 5 hours and 5.0001 hours should be about 0.0002, and so on.

In this example, the ratio (probability of dying during an interval)/(interval duration) is approximately constant, and equals 2 per hour (or 2hour^-1). For example, there is a 0.02 probability of dying in the 0.01 hour interval between 5 and 5.01 hours, and (0.02 probability/0.01 hours) = 2hour^-1. This quantity 2hour^-1 is called the probability density of dying at around 5 hours. Therefore, the probability that the bacterium will die within 5 hours can be written as (2 hour^-1) dt. This is the probability that the bacterium will die within an infinitesimal time window of around 5 hours, where dt is the duration of this window. For example, the probability that you will live more than 5 hours, but less than (5 hours + 1 nanosecond), is (2 hours-1)×(1 nanosecond) ≈ 6×10-13 (using the unit conversion 3, 6×1012 nanoseconds = 1 hour).

There is a probability density function f with f(5hours) = 2 hours^-1. The integral of f over any time window (not only infinitesimal windows but also large windows) is the probability that the bacteria will die in that window.

Probability density function for normal distribution.

Additional bibliography

• Billingsley, Patrick (1979). Probability and Measure (in English). New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
• Casella, George; Berger, Roger L. (2002). Statistical Inference (in English) (Second edition). Thomson Learning. pp. 34-37. ISBN 0-534-24312-6.
• Stirzaker, David (2003). Elementary Probability (in English). ISBN 0-521-42028-8. (requires registration). Chapters 7 to 9 are about continuous variable.