Precession

The precession or precession movement is the movement associated with the change of direction in space, experienced by the instantaneous axis of rotation of a body.

We have an example of precession in the movement made by a spinning top or spinning top. When its axis of rotation is not vertical, the top has a "pitch" movement similar to that of precession.

More exactly, a pure precession is that movement of the axis of rotation that keeps its second Euler angle (nutation) constant. This movement of nutation also occurs on the Earth's axis.

There are two types of precession: precession due to external moments, and precession without moments of external forces.

Precession without external moments

This movement occurs when a body is moving around an axis that is neither the one with the greatest moment of inertia nor the one with the least moment of inertia. The precession can be accompanied by other movements of rotating bodies such as nutation. There is a special type of curves on the surface of the object, called polodia and herpolodia, which describe the movement of the object.

Precession due to external moments

Angles used to describe the orientation of the hair.

Precession in a solid of revolution

His name is symmetrical hair in free movement to a rigid solid of revolution, with two of its main inertia moments equal I1=I2I was. I was. I3{displaystyle I_{1}=I_{2}neq I_{3}}}. As in a symmetrical peonza you can arbitrarily choose the axes 1 and 2, it is appropriate to take advantage of that fact to simplify the expressions by taking the axis 1 parallel to the nodal line of the Euler angles, which is equivalent to /25070/ = 0.

Which leads to the angular velocities in the non-inertial reference system being given by:

ω ω ={ω ω 1ω ω 2ω ω 3!={θ θ ! ! φ φ ! ! without θ θ φ φ ! ! # θ θ +END END ! ! !{displaystyle {boldsymbol {omega }}={begin{Bmatrix}omega _{1}omega _{2}omega _{3}{Bmatrix}}{Bmatrix}{Bmatrix}{Bmatrix}{dot {theta }{

The kinetic rotation energy of a symmetrical pawn (I1=I2I was. I was. I3{displaystyle scriptstyle I_{1}=I_{2}neq I_{3}}) can be expressed in terms of the Euler angles simply:

Ec=12(I1ω ω 12+I2ω ω 22+I3ω ω 32)=I12(φ φ ! ! 2without2 θ θ +θ θ ! ! 2)+I32(φ φ ! ! # θ θ +END END ! ! )2{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF00}{cHFFFFFF00} {cHFFFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH}{cH}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cHFFFFFFFFFFFF}{c}{cH00}{cH00}{cH}{cH00}{cH00}{cH}{cH

On the other hand, if the Z axis of the reference system is taken aligned with the angular momentum of the rigid body, the angular momentum components and the relationship with the angular velocity are:

L={0Lwithout θ θ L# θ θ !=[chuckles]I1000I1000I3]{ω ω 1ω ω 2ω ω 3!={I1θ θ ! ! I1φ φ ! ! without θ θ I3(φ φ ! ! # θ θ +END END ! ! )!♪ I'm gonna go ♪

Writing these equations component by component, we have:

θ θ ! ! =0I1φ φ ! ! =LI3ω ω 3=I3(φ φ ! ! # θ θ +END END ! ! )=L# θ θ {displaystyle {dot {theta }}=0qquad I_{1}{dot {dot}=Lqquad I_{3}omega _{3}=I_{3}({dot {phi }}}{cos theta +{dot {psi }})=Lcos theta }}}}

The first equation tells us that in the free movement of a symmetrical spinning top it does not wobble; that is to say, there is no movement of nutation since the angle formed by the axis of rotation and the angular momentum remains constant in the movement. The second describes the precession movement according to which the axis of rotation (which coincides with the direction of angular velocity) revolves around the direction of angular momentum (Z axis). The third equation gives the speed of rotation of the solid about its third axis of inertia.

Gyroscope

Remember that angular momentum is a vector whose module is the product of the moment of inertia of the body around the axis of rotation, multiplied by the angular velocity. The direction of the vector is the same as that of the vector associated with the angular velocity and is given by the right-hand rule. The basic equation of the angular momentum of a body is:

dLdt=M{displaystyle {dmathbf {L} over dt}=mathbf {mathbf {M} } }

where L{displaystyle scriptstyle {mathbf {L} }} is the angular moment of the body and M{displaystyle scriptstyle {mathbf {M} }} is the time of force applied to the body. This equation corresponds, in the linear movement, to the equation F=dpdt{displaystyle scriptstyle {mathbf {F} ={dmathbf {p} over dt}}}} where F{displaystyle scriptstyle {mathbf {F}}}} is the force applied to a body and p=mv{displaystyle scriptstyle {mathbf {p} =mmathbf {v} }}}} is the linear moment of the body.

When the moment of force is parallel to the angular momentum, that is, parallel to the axis of rotation, nothing changes in the rotation. On the other hand, a component of the moment, perpendicular to the axis of rotation, does not change the magnitude of the angular velocity but its direction, that is, the direction of the axis of rotation of the body.

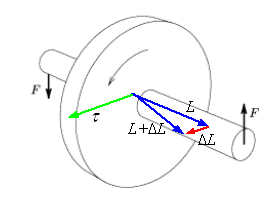
Consider the body in rotation of the right image. When a dynamic moment is applied as indicated by the forces drawn, the direction of the variation of the angular moment is indicated in the drawing. This variation is perpendicular to the angular moment and parallel to the moment. The variation of L{displaystyle scriptstyle {mathbf {L} }} during a time interval Δ Δ t{displaystyle scriptstyle {Delta t}} is:

Δ Δ L=MΔ Δ t{displaystyle Delta mathbf {L} =mathbf {M} Delta t}

Note that Δ Δ L{displaystyle Delta mathbf {L} ,} has the same direction as M{displaystyle scriptstyle {mathbf {M} }}. The angle Δ Δ φ φ {displaystyle scriptstyle {Delta phi }} that the new angular moment L+Δ Δ L{displaystyle scriptstyle {mathbf {L} +Delta mathbf {L}}}} with the precedent L{displaystyle scriptstyle {mathbf {L} }} fulfills that:

So... Δ Δ φ φ =Δ Δ LL{displaystyle tan {Delta phi }={Delta L over L over}

If the quotient Δ Δ LL{displaystyle scriptstyle {Delta L over L}} is small (e.g. less than 5 ° in magnitude, typically caused by a time interval Δ Δ t{displaystyle scriptstyle {Delta t}} small), angle Δ Δ φ φ {displaystyle scriptstyle {Delta phi }} can be obtained from the approximation of the above equation shown below:

Δ Δ φ φ ≈ ≈ Δ Δ LL{displaystyle Delta phi approx {Delta L over L}}}

La speed of pressure gyroscope is the angular speed of the vector L{displaystyle scriptstyle {mathbf {L} }} which is the same as the rotation axis of the latter:

Precession speed =Ω Ω =Δ Δ φ φ Δ Δ t=ML{displaystyle =Omega ={Delta phi over Delta t}={M over L}}

Precession velocity is an angular velocity and is measured in radians/second.

The speed of precession is smaller the larger the angular momentum of the body.

Precession can be intuitively explained by the "square wheel model".

Spinning top or spinning top

Figure 1.

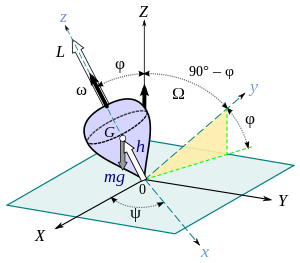
If the rotation axis of the thrompo, z, shape a certain angle φ φ {displaystyle ,phi } with the vertical, as usually happens, that axis moves in space generating a conical surface of revolution around the fixed vertical axis Z. This rotation axis movement receives the name of precession of the pawn and axis Z is the axis of precession. Generally, the angle φ φ {displaystyle ,phi } it varies periodically during the precession movement of the peonza, so that the rotation axis is approaching and moving away from the axis of precession (tenth of the trumpet); this movement is called nutation and angle φ φ {displaystyle ,phi } It's called a tie angle. In the elementary study that follows we will not take into account this last movement; i.e., we will consider a constant nut angle.

We will use two references to describe the movement of the trompo. One of them is the fixed reference XYZ, originating in point O (stationary) of the rotation axis of the trompo. The other reference is the mobile reference xyzwhose origin is also point O (stationary). We'll match the axis. z with the rotation axis of the trompo; the axis x we choose it so that it stays always horizontal, content on the plane XY. The angle END END {displaystyle ,psi } that forms in every moment the axis x with the shaft X receives the name of [[announce of precession]]. Consequently, the axis and will always be contained in the plane defined by the axes z and Zas shown in Figure 1, forming an angle φ φ {displaystyle ,phi } with the plane XY. Note that the reference xyz it is not sympathetic with the trumpet, i.e., it is not carried by the rotation of this, but it presents a rotation with respect to the fixed reference XYZ with a certain angular speed Ω Ω {displaystyle ,omega } called angular pressure speed.

As when applying the equation of rotational motion of the rigid body, M = dL/dt, both the external moment (M) and angular momentum (L) must be referred to the same fixed point in an inertial referential (or to the CM of the body), we will take point O as origin or reduction center.

Figure 2.

Since the top is spinning, with an intrinsic angular velocity ω, about the principal axis of inertia z, its angular momentum will be parallel to the angular velocity (or that is, will be parallel to the z axis), and is given by

(1)L=Izzω ω {displaystyle L=I_{zz}omega ,}

On the other hand, the external moment acting on the top is due to the weight mg acting at the center of gravity G and is equal to the vector product

(2)M=OG× × mg{displaystyle mathbf {M} ={mbox{OG}}}times mmathbf {g ,}

so that the external moment M turns out to be perpendicular to the rotation axis, so that M L{displaystyle mathbf {M} mathbf {bot } mathbf {L} }. The module of the time applied is

(3)M=mghwithout φ φ {displaystyle M=mghsin phi ,}

where h=OG is the distance between the stationary point of the top (the end of its spike) and its center of gravity. The direction of M is that of the x axis.

Since the external momentum applied to the top is not zero, the angular momentum will not remain constant. During an infinitesimal time interval dt the infinitesimal change experienced by angular momentum is equal to

(4)dL=Mdt{displaystyle dmathbf {L} =mathbf {M} dt}

so that the change dL in angular momentum always has the same direction as the applied moment M (in the same way that the change in momentum always has the same direction as the force). Since momentum M is perpendicular to angular momentum L, the change dL in angular momentum is also perpendicular to L b>. Consequently, the angular momentum vector changes direction, but its magnitude remains constant (figure 2). Naturally, since the angular momentum always has the direction of the axis of rotation, this will also change its orientation in space in the course of time.

The end of the angular moment L describes a circle of radio Lwithout φ φ {displaystyle ,Lsin phi }, around the fixed axis Z and in a time dt said radio experiences an angled displacement. The angular pressure speed Ω is defined as the angular speed with which the axis rotates z around the fixed axis Z. This is it.

(5)Ω Ω =dEND END dt{displaystyle Omega ={frac {dpsi }{dt}}}}

y is represented by a vector located on the Z axis.

Since L is a vector of constant magnitude that precesses around the Z axis with an angular velocity Ω, we can write the differential equation of rotational motion in the form

(6)M=dLdt=Ω Ω × × L{displaystyle mathbf {M} ={frac {dmathbf {L}{dt}}}={boldsymbol {Omega }}times mathbf {L} } }

obtaining for the module of the moment

(7)M=Ω Ω Lwithout φ φ {displaystyle M=Omega Lsin phi ,}

expression from which we will clear Ω to have

(8)Ω Ω =MLwithout φ φ =mghL=mghIzzω ω {displaystyle Omega ={frac {M}{Lsin phi }}}={frac {m}{L}}}={frac {mgh}{I_{zz}omega }}}}}}}

where we have substituted expressions (1) and (2) for angular momentum and momentum, respectively. The angular velocity of precession, Ω, turns out to be inversely proportional to the angular momentum (L) or to the intrinsic angular velocity (ω), so that if this or this is large, that will be small.

Note that the angular velocity of precession does not depend on the angle of inclination of the top. This property is very important in the foundation of nuclear magnetic resonance and its applications.

But why doesn't the top fall? The answer is that the vertical force exerted on it by the ground (at the O end of the spike) is exactly equal to the weight of the top, so the resultant vertical force is zero. The vertical component of momentum will remain constant, but because momentum is not zero, angular momentum changes with time. If the top were not rotating, when leaving it there would be no angular momentum and after an infinitesimal time interval, dt, the angular momentum dL acquired, by virtue of of the couple of forces acting on it, would have the same direction as the vector M; that is, it would fall. But if the top is initially in rotation, the variation of the Angular momentum, dL, produced by the couple, adds vectorially to the angular momentum it already has, and since dL is horizontal and perpendicular to L, the result is the precession described above.

Figure 3.

The results obtained in our discussion of top motion are only approximate. They are correct if ω is very large compared to Ω (a situation compatible with eq. [7]). The reason is that if the top is precessing about the fixed vertical axis Z it will have angular momentum about that axis, so the total angular momentum will not simply be I_zzω, as we assumed. However, if the precession is very slow, the angular momentum corresponding to that precession can be neglected, as we have implicitly done in our previous calculations.

On the other hand, a more detailed discussion would show us that in general the angle of precessionφ φ {displaystyle ,phi } does not remain constant, but fluctuates between two fixed values, so that the end of the vector L, at the same time you press around Z, oscillates between two circles, as shown in figure 3, describing the indicated path.

To understand the reason for these oscillations we must consider the way in which the precession movement originates. If we initially keep the orientation of the axis of rotation z fixed (supporting its upper end) the weight of the top will be compensated by the normal reaction N at point O plus the normal reaction in the support of the upper end of the axis, so that it will turn out to be N < mg. If, once the top has acquired a rapid rotational movement, we leave the axis, then even an instant later it will be N < mg, so we have a resultant force that is vertical and directed downward. The top begins to fall, but at that moment the precession begins. As a consequence of the falling movement, the top's spike rests on the ground with more force, so that the vertical reaction force N increases, which eventually becomes greater than the weight. When this happens, the center of mass of the top begins to accelerate upward. The process is repeated, and the movement is made up of a precession accompanied by an oscillation of the axis of rotation up and down, which is called nutation. Nutation, like precession, contributes to the total angular momentum, but in general its contribution is still less than that of precession.