Potential energy

ImprimirCitar

The potential energy is the mechanical energy associated with the location of a body within a force field (e.g. gravitational, electrostatic, etc.) or the existence of a force field inside of a body (elastic energy). The potential energy of a body is a consequence of the fact that the system of forces acting on it is conservative.

Regardless of the force that originates it, the potential energy possessed by the physical system represents the "stored" by virtue of its position and/or configuration, as opposed to the kinetic energy it has and which represents its energy due to movement. For a conservative system, the sum of kinetic and potential energy is constant, which justifies the name of conservative forces, that is, those that make energy "conserve". The concept of potential energy can also be used for physical systems in which dissipative forces intervene, and therefore do not conserve energy, except that in that case the total mechanical energy will not be constant, and to apply the principle of conservation of energy. it is necessary to account for energy dissipation.

The value of potential energy always depends on the reference point or configuration chosen to measure it, for this reason it is sometimes said that physically only the variation of potential energy between two configurations matters..

Potential energy intervenes as mentioned in the principle of conservation of energy and its field of application is very general. It is present not only in classical physics, but also in relativistic physics and quantum physics. The concept has also been generalized to particle physics, where complex potentials have been used in order to also include the energy dissipated by the system.

Introduction

While kinetic energy ( ${displaystyle E_{c}}$ ) of a body is a physical property that depends on its movement, the potential energy ( ${displaystyle E_{p}}$ ), instead, is a concept of energy that will depend on the type of interaction that is exercised over the body, its position and the configuration in the space of the above body or bodies on which it is applied. Thus in an ideal situation in which objects that constitute the physical system under study are absent from friction, then the sum of both energies, kinetic and potential, will represent the total energy of the system, $E$ and it will be preserved, regardless of the position or positions that the system is occupying in time.

The notion of potential energy relates to the work done by forces on the physical system to move it from one position to another of space. The potential energy function will depend significantly on the type of force field or interaction that acts on the system. For example, the gravitation force, the electromagnetic, responsible for electrical and magnetic interactions, or elastic (derivada de la electromagnetica). If the work does not depend on the path followed, then by force ${displaystyle {overrightarrow {F}}}$ it is called conservation and work $W$ expresses the difference of potential energy ${displaystyle E_{p_{A}}-E_{p_{B}}}$ between the starting position (A) and the arrival position (B).

{displaystyle W_{AB}=int _{A}^{B}{overrightarrow {F}}cdot ,{overrightarrow {dl}}=E_{p_{B}}-E_{p_{A}}qquad qquad }

The potential function is also used $V$ instead of potential energy ${displaystyle E_{p}}$ to represent the work done by the basic unit of the interaction. If, for example, interaction is gravitational, it would be mass unity and in the case of electrical interaction, the load unit.

The potential energy function, and especially the potential function, are of great interest in physics not only when they are applied to interactions that are important on our scale, such as gravitational, electromagnetic, and elastic (derived from electromagnetic), but also when studying any type of force or interaction, even in quantum physics when trying to solve the dynamics of a physical system using the Schrödinger equation. It is applied, for example, to atomic physics in the Obtaining the electronic states of the atom or in molecular physics, to obtain the electronic, vibration, vibration-rotation and rotation states of the molecule, as well as in solid state physics. It is also applied in nuclear physics.

In other more general formulations of physics, the potential function also plays an important role. Among them, the Lagrangian and Hamiltonian formulations of mechanics.

Gravitational Potential Energy

The cars of a roller coaster reach their maximum gravitational potential energy in the highest part of the route. By descending, it becomes kinetic energy, becoming maximum by reaching the lowest point of its trajectory (and the minimum potential energy). Then, by rising again due to the inertia of the movement, the transfer of energies is reversed. If an insignificant friction is assumed, the total energy of the system remains constant

Gravitational potential energy is defined as the energy possessed by bodies due to the fact that they have mass and are located at a certain mutual distance. Between the masses of great magnitudes attractive forces are exerted, of greater intensity the greater they are. Applied, for example, to planetary motion, the greater mass is that of the sun, which creates a gravitational force field that acts on the lesser masses of the planets. In turn, each planet creates a gravitational force field that acts on the smaller masses that are close to the planet, the satellites.

The work done to carry a test mass m in the presence of another mass M, source of the gravitational field, from a point A to another B, is the difference of the potential energy of the mass m at the starting point A minus the potential energy at the arrival point B. The aforementioned work does not depend on the path followed but only on the initial and final points. As the gravitational force and the gravitational field (the gravitational force on the unit mass) enjoy this property, the field is called a conservative field and it makes perfect sense to obtain the gravitational potential, derived from the field created by the mass M, as well as the gravitational potential energy derived from the gravitational force between the masses m and M.

If an M mass is considered at the origin of the coordinate system as a source of the gravitational field and the infinite, point at which any m mass has a null potential energy, the potential energy is the work necessary to carry the m mass from infinity to a certain point A defined by the coordinate $r$ (the distance from point A to the origin of coordinates).

${displaystyle W=E_{p_{A}}-E_{p_{infty }}=}$ ${displaystyle Delta E_{p}=-int _{infty }^{A}F_{g}cdot ,dr=-int _{infty }^{A}{frac {Gcdot Mcdot m}{r^{2}}}cdot ,dr=Gcdot Mcdot mcdot leftlbrack {frac {1}{r}}rightrbrack _{infty }^{A}={frac {Gcdot Mcdot m}{r_{A}}}=E_{p_{A}}qquad qquad [1]}$

Where: ${displaystyle E_{p}}$ is the gravitational potential energy of the mass $m$ , whose value depends on the distance $r$ between the test mass $m$ and the mass $M$ which generates the gravitational field, and is measured in July ( $J$ ). On the other hand, ${displaystyle F_{g}={frac {Gcdot Mcdot m}{r^{2}}}}$ is the gravitational force on the test mass $m$ situated at a distance $r$ of the mass $M$ that creates the gravitational field and is measured in newtons ( $N$ ). Plus, $G$ is the constant universal gravitation, whose value is ${displaystyle G=6.673times 10^{-11};left({cfrac {{text{N}}cdot {text{m}}^{2}}{{text{kg}}^{2}}}right)}$ . Finally, $M$ and $m$ are measured in kilograms ( ${displaystyle kg}$ ) $R$ is the distance between the two masses, measured in meters ( $m$ )

The equation [1] that represents potential energy ${displaystyle E_{p_{A}}}$ of the m and M masses when a distance is separated ${displaystyle r_{A}}$ , it is applicable to both punctual masses and masses with spherical symmetry, the distance between them, the one between the centers of these spheres.

Potential energy near the Earth's surface

The potential energy that possesses a mass $m$ at a height ${displaystyle h}$ on the terrestrial surface is worth:

{displaystyle Delta E_{p}=mcdot gcdot hqquad qquad [2]}

This expression is a particular case of the previous equation [1]. This case occurs when the mass is at a small height on the surface of the earth. To prove it, just apply the expression [1] and consider the variation of potential energy between heights on the surface of the earth, ${displaystyle h_{1}}$ and ${displaystyle h_{2},(h_{1}ll R_{t},h_{2}ll R_{t}}$ and $h_{1})}" xmlns="http://www.w3.org/1998/Math/MathML">h2▪h1){displaystyle h_{2} verbalh_{1})}h_{1})}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/815c36aa5b96fdf540623a80376123773fd3ca7b" style="vertical-align: -0.838ex; width:8.79ex; height:2.843ex;"/>$ being ${displaystyle R_{t}}$ the radius of the earth.

{displaystyle Delta E_{p}=E_{p2}-E_{p1}=Gcdot Mcdot mcdot left({frac {1}{R_{t}+h_{1}}}-{frac {1}{R_{t}+h_{2}}}right)=}

{displaystyle =E_{p2}-E_{p1}=Gcdot Mcdot mcdot {frac {(h_{2}-h_{1})}{R_{t}^{2}+R_{t}cdot (h_{2}+h_{1})+h_{1}cdot h_{2}}}approx Gcdot Mcdot mcdot {frac {h_{2}-h_{1}}{R_{t}^{2}}}qquad qquad [3]}

In this case, the products ${displaystyle R_{t}cdot h_{2},R_{t}cdot h_{1}}$ and ${displaystyle h_{1}cdot h_{2}}$ are very small compared to ${displaystyle R_{t}^{2}}$ and therefore can be despised in the equation [3].

Calling ${displaystyle g=Gcdot Mcdot {frac {1}{R_{t}^{2}}}}$

{displaystyle E_{p2}-E_{p1}=mcdot gcdot (h_{2}-h_{1})}

If taken ${displaystyle h_{1}}$ like the origin of potential energies, for example, at sea level and calling ${displaystyle h_{2}=h}$ :

${displaystyle Delta E_{p}=mcdot gcdot h}$

From previous development it follows that ${displaystyle hll R_{t}}$ the ultimate approach is adequate.

Escape Velocity

The exhaust speed is the minimum speed required for a mass body $m$ Get out of the gravitational attraction.

The gravitation force is conservative. Potential energy ${displaystyle E_{p}(r)}$ of a mass $m$ is:

{displaystyle E_{p}(r)=-Gcdot {frac {mcdot M}{r}}}

For the body to escape the action of the gravitational field total energy ${displaystyle E_{t}}$ of the same must be positive or null, that is, it must happen that kinetic energy exceeds or, at least equals, potential energy. In the threshold case we will be calculating the exhaust speed. It can be calculated in the case of Earth.

{displaystyle E_{T}=0}

${displaystyle E_{t}=E_{c}+E_{p}=0Rightarrow {frac {1}{2}}cdot mcdot v_{e}^{2}=Gcdot {frac {mcdot M}{r}}}$

{displaystyle v_{e}={sqrt {frac {2cdot Gcdot M}{r}}}={sqrt {2gr}}}

{displaystyle (m/s)}

where $r$ is the radial distance or position of the mass body $m$ regarding the mass $M$ which generates the gravitational field

Earth surface exhaust speed

${displaystyle G=6.674cdot 10^{-11};{cfrac {{text{N}}cdot {text{m}}^{2}}{{text{kg}}^{2}}}}$

${displaystyle M_{T}=5,97cdot 10^{24}}$ ${displaystyle kg}$

${displaystyle R=6,37cdot 10^{6}}$ $m$

Substituting the data we obtain:

{displaystyle v_{e}={sqrt {frac {2cdot Gcdot M_{T}}{R}}}={sqrt {frac {2cdot 6,67cdot 10^{-11}cdot 5,97cdot 10^{24}}{6,37cdot 10^{6}}}}approx 11,17cdot 10^{3}}

{displaystyle mcdot s^{-1}}

If the mobile exceeds the escape velocity, it would even more easily abandon the action of the terrestrial gravitational field.

Equipotential surfaces

The gravitational potential is defined as the potential energy per unit mass:

{displaystyle V={frac {E_{p}}{m}}}

And therefore you get:

{displaystyle V(r)={frac {Gcdot M}{r}}}

Where $V$ is the potential energy of mass unity, or potential, at a distance $r$ of the mass $M$ . Units $V$ in the S.I. are ${displaystyle {frac {J}{kg}}}$ .

G is the universal gravitational constant.

M is the mass of the object that creates the field and therefore will be measured ${displaystyle kg}$ .

If M is punctual or spherical in geometry, the equipotential surfaces (constant potential surfaces) are the family of spheres defined by the family of surfaces:

{displaystyle V_{i}={frac {Gcdot M}{r_{i}}}=C_{i}\qquad i=1,2,3...}

being ${displaystyle C_{i}}$ arbitrary constants whose numerical value represents the gravitational potential associated with each value of position ${displaystyle r_{i}}$ .

The earth's gravitational equipotential surfaces are all spheres with the center of the Earth.

Examples of Gravitational Potential Energy

Animation of a ball on a roller coaster

Roller Coaster

The drawing of a roller coaster on a plane can be interpreted as the representation of the potential energy function ${displaystyle E_{p}}$ of a body in the gravitational field. The more a mobile the Russian mountain rises, the greater its potential energy and the less its kinetic energy ${displaystyle E_{c}}$ , and therefore moves slower. In the relative maximums of that function (the peaks of the Russian mountain) its potential energy will be higher than in the points of its environment. These points will be called unstable mechanical balance points, as if an object is deposited in them ${displaystyle v=0}$ the object will always tend to move away. On the other hand, if we place it in the minimums of the function (the valleys of the Russian mountain), the mobile that abandons them in one or another sense will always tend to return to them, are the points called stable balance points. Like mechanical energy $E$ of the body is preserved ${displaystyle E=E_{c}+E_{p}=E_{cmax}=E_{pmax}}$ in the figure.

Pendulum

In the case of a pendulum, whose movement can reach a height ${displaystyle h}$ from its lower position, you can also check the energy conservation law. At the highest points (height h), where the potential energy is maximum, the speed of the pendulum is null and the movement changes sense. On the other hand, the lowest position, which can be called $P$ , will be that with greater kinetic energy and maximum speed but with minimal potential energy. Position $P$ can be taken as the source of potential energy (can be associated with a potential null energy).

Animation of a pendulum that reaches a height h

Application to planetary motion

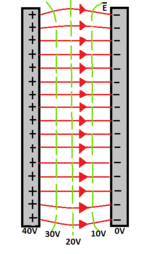
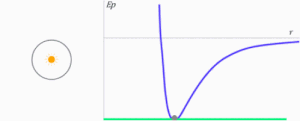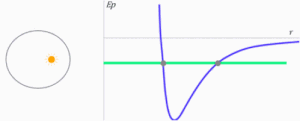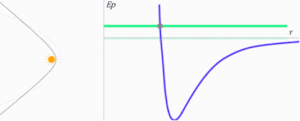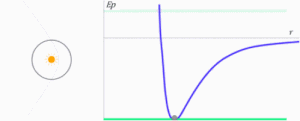
The gravitational potential energy diagram of the planets allows to determine the shape of its path around the sun. For an average energy, which corresponds to the potential well region, the trajectory of the planet is an ellipse of r1 and r2 radios (first law of Kepler)

Gravitational potential energy influences the shape of the orbits of planets and other celestial bodies of the Solar System. The type of orbit is a conical and its shape will depend on total mechanical energy $E$ of the body. Potential energy is negative or positive, while kinetic energy is always positive.

The total energy of the body, being the sum of both, can be negative, positive or null. It is easy to recognize the shape of orbits with the help of the potential energy diagram ${displaystyle E_{p}(r)}$ or potential ${displaystyle V(r)}$ . The green line serves to indicate in each case the value of the total energy of the planet or the celestial body in the animation that follows. The Sun is always in position ${displaystyle r=0}$ and represents the origin of the gravitational force.

The gravitational potential energy diagram of the celestial bodies of a solar system allows to determine the shape of their trajectory around the star. The animation describes the different trajectories of the celestial body, depending on its total energy, around its sun

If total energy is negative and of absolute value equal to half of the potential energy (minimum of the curve), the trajectory is a circle with center in the origin of the forces.

{displaystyle {color {Black}E}={color {Black}-{frac {1}{2}}G{frac {Mm}{r}}}}

If total energy is greater than that required for the orbit to be circular, but still remains negative, the orbit becomes an outer ellipse to the circular orbit. In this case, the force centre will be one of the focus of that ellipse.

<math alttext="{displaystyle {color {Black}-{frac {1}{2}}G{frac {Mm}{r}}}<{color {Black}E}− − 12GMmr.E.0{displaystyle {color {Black}-{frac {1}{2}}}G{frac {Mm}{r}}}}}}}}}{color {Black}E}{color {Black}}<img alt="{displaystyle {color {Black}-{frac {1}{2}}G{frac {Mm}{r}}}<{color {Black}E}

If total energy is less than the one needed to describe a circular orbit, there will be no movement as a negative kinetic energy.

<math alttext="{displaystyle {color {Black}E}E.− − 12GMmrnoresporsible{displaystyle {color {Black}E}{color {Black}-{frac {1}{2}{2}G{frac {Mm}{r}}}}{qquad no possible}<img alt="{displaystyle {color {Black}E}

If total energy becomes zero or positive, the trajectory ceases to be closed and the body will escape from the gravitational attraction exercised by M. Yes ${displaystyle E=0}$ , kinetic energy is, in absolute value, equal to potential energy. It represents the minimum energy necessary for the body to escape from such attraction, then the speed of escape and its path will be a parable with its focus in the center of forces. The path will then be open.

{displaystyle {color {Black}E}=0Rightarrow E_{c}=-E_{p}}

If total energy is positive it is because at absolute values its kinetic energy is greater than its potential energy. Therefore, its speed exceeds the exhaust speed and its trajectory will be a hyperbola, a conical also open.

0Rightarrow E_{c}>-E_{p}}" xmlns="http://www.w3.org/1998/Math/MathML">E▪0⇒ ⇒ Ec▪− − Ep{displaystyle {color {Black}E}{pos(Rightarrow E_{c}{c}{p}}}0Rightarrow E_{c}>-E_{p}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0bee798c60f1dcdbb59a8bbe38dc14fa5cba5dbe" style="vertical-align: -1.005ex; width:19.991ex; height:2.843ex;"/>

Elastic potential energy

This catapult makes use of potential elastic energy

Main article: Potential elastic energy

Elasticity is a property of certain materials by which, once deformed, stretched or separated from their initial position, they can recover their original state, or equilibrium. The restoring forces responsible for recovery are elastic forces such as springs, rubber bands, or musical instrument strings. Many ancient war machines used this type of energy to launch objects from a distance, such as the bow that shoots an arrow, the crossbow or the catapult. The vibrations or oscillations of material objects, caused by elastic forces, are the source of sound waves. The recuperative forces, when the object recovers its original shape with hardly any damping or deformation, are conservative and an elastic potential energy can be derived, which added to the kinetic energy, allows obtaining the mechanical energy of the object.

A material is said to be more elastic when it returns to its equilibrium position more precisely. A strip of rubber is easy to stretch, springing back to close to its original length when released, but it is not as elastic as a guitar string. The guitar string is more difficult to stretch, but it has better recovery than the rubber strip, because it returns to its original length more precisely.

A spring is an example of an elastic object that returns to its original shape precisely: when stretched it exerts an elastic force that tends to return it to its original length. It is verified experimentally that this restoring force is proportional to the stretched length of the spring. The way to express this proportionality between the force and the amount stretched is through Hooke's law. The coefficient of proportionality in this deformation depends on the type of material and the geometric shape that is considered. For solids, the elastic force is generally described in terms of the amount of deformation caused by the tensile force resulting from a given stretch, called the Young's or elastic modulus. For liquids and gases it is expressed by the pressure variation capable of producing a volume variation and is called the modulus of compressibility. For springs and cables an elastic constant k is used.

Hooke's law roughly describes the elastic properties of bodies and on which the elastic response conditions are based, close to equilibrium conditions, of deformable material subjected to stretching or compression. It has numerous applications and in all of them the responsible force is obtained with the aforementioned law in an approximate way, and the resulting response movement is that of the harmonic oscillator.

Hooke's Law

Representation of the law of Hooke in a ball moving on a surface without friction.

One of the properties of the elasticity of a solid or a fluid, when stretched or deformed, is that said stretching or deformation is proportional to the applied force. That is, it would take twice as much force to produce a double stretch. This linear dependence of the displacement with the applied force is known as Hooke's Law.

Robert Hooke was an English scientist, both theoretical and experimental, a tireless polemicist, with a creative genius of the first order, who was part of the creative nucleus of the Royal Society. In 1660, while working as an assistant to Robert Boyle, he formulated what is now called Hooke's Law of Elasticity. If this law is applied to a mass attached to a spring, stretching it a length x from its equilibrium position, Hooke's law states that the block will then be subjected to an elastic restoring force of the shape:

${displaystyle {vec {F_{el}}}=-kx{vec {u_{x}}}}$ ,

being k the elastic constant of the spring and x the displacement suffered with respect to its equilibrium position x=0. The minus sign of the equation reflects that the elastic force is a restoring force that always tends to bring the solid to its equilibrium position, in this case x=0.

Deduction of elastic potential energy

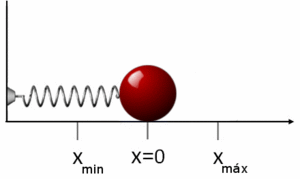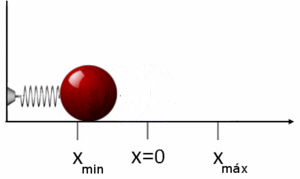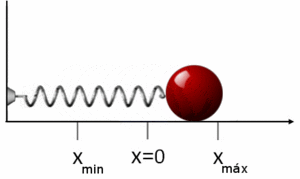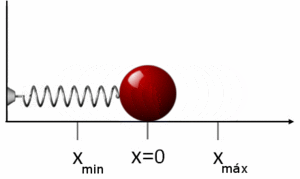
If a mass m is attached to one end of the spring and is separated a distance x from its equilibrium position, x=0, it will begin to oscillate with a simple harmonic motion. In this movement the block has kinetic energy and potential energy. Since the elastic force that satisfies Hooke's law is a conservative force, the potential energy function can be derived, under the action of the elastic force of the spring. Thus, the work done in stretching the spring a distance x from its equilibrium position, opposing the force of the spring is:

${displaystyle W=E_{p}(x)=int _{0}^{x}-F_{x}dx=int _{0}^{x}-(-kx)dx={frac {1}{2}}kx^{2}qquad qquad }$

This work represents potential energy E_p that has the block in the position x. This has been agreed to associate the E_p=0 to position x=0 (source of potential function). If work is now calculated to move the block from a position $x_{1}$ another $x_{2}$ , it is verified that this only depends on the initial and final positions:

${displaystyle W=E_{p}(x_{2})-E_{p}(x_{1})=int _{x_{1}}^{x_{2}}-kxdx={frac {1}{2}}k(x_{1}^{2}-x_{2}^{2})}$

In the figure you can see the potential energy function E_p(x) as a parable focused on x=0, position function x. The slope line -k, is the corresponding elastic force ${displaystyle {vec {F_{el}}}=-kx{vec {u_{x}}}}$ . At the same time the stretched amount of the dock is represented depending on its position x. If with a force F x displacement occurs, with force 2F displacement is also double, 2x. The negative part of the axis x represents the displacement of the dough when the dock is compressed.

Elastic potential energy curve and corresponding force applied to a ball response subject to a spring

Properties of the Potential Energy Curve

Earring of the curve ${displaystyle E_{p}(x)}$ :

${displaystyle Fuerza:{vec {F}}=-{frac {dE_{p}}{dx}} {vec {u_{x}}}=-kx{vec {u_{x}}}}$

Yeah. $0}" xmlns="http://www.w3.org/1998/Math/MathML">x▪0{displaystyle x 2005}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$

0quad 'pendientequad positiva'}" xmlns="http://www.w3.org/1998/Math/MathML">dEpdx=kx▪0♫pendienteporsitiva♫{displaystyle {frac {dE_{p}}{dx}}=kx/20050quad 'pendentquad positive'}0quad 'pendientequad positiva'}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/89d0704fa22757946582c057dc7b456807b38852" style="vertical-align: -2.005ex; width:38.998ex; height:5.676ex;"/>

Yeah. $<math alttext="{displaystyle xx.0{displaystyle x vis0} <img alt="{displaystyle x$

<math alttext="{displaystyle {frac {dE_{p}}{dx}}=kxdEpdx=kx.0♫pendientenegativa♫{displaystyle {frac {dE_{p}}{dx}}=kx vis0quad 'pendientequad negative'}<img alt="{displaystyle {frac {dE_{p}}{dx}}=kx

Balance point:

{displaystyle {frac {dE_{p}}{dx}}=kx=0Rightarrow x=0}

0}" xmlns="http://www.w3.org/1998/Math/MathML">d2Epdx2=k▪0{displaystyle {frac {d^{2}E_{p}}{dx^{2}{2}}=k HCFC}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f2129229d8527420607de5190dd57efc8f079705" style="vertical-align: -2.171ex; width:14.453ex; height:6.176ex;"/>

It's a minimum.

Electrostatic potential energy and electric potential

Main article: Electrostatic potential

The variation of potential energy represents a work done by a conservative force. Just as the force of attraction between two masses is conservative, also the power or strength of Coulomb ${displaystyle F_{el}}$ between two loads is conservative, being repulsive if they have the same sign and attraction if they are of opposite sign. The objects that repel have greater potential energy the less the distance between them, and if they are attracted the greater their potential energy the greater the distance between them, as we will see below.

The work of a conservative force is equal to the difference between the initial value and the final value of a function, the potential energy, since it will only depend on the initial and final positions and not on the trajectory followed. Electrostatic forces caused by electric charges are conservative and the work done by these forces will not depend on the path followed:

{displaystyle W=int _{A}^{B}{vec {F}}_{el}cdot d{vec {l}}=E_{pA}-E_{pB},!}

being ${displaystyle E_{p}}$ the potential energy function ${displaystyle E_{pA}}$ and ${displaystyle E_{pB}}$ potential energy values in positions A and B.

Variables involved in electrical work performed when moving a q charge, in presence electric field created by another Q load

To calculate the work ${displaystyle W}$ due to electrical or electrostatic force, ${displaystyle F_{el}}$ :

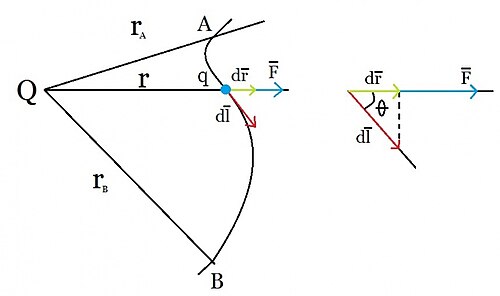
{displaystyle {overrightarrow {F}}_{el}={frac {1}{4pi varepsilon _{0}}}{frac {Qq}{r^{2}}}{overrightarrow {u}}=q{overrightarrow {E}}}

To transfer the load $q$ from position A to position B first need to express infinitesimal work ${displaystyle dW}$ as the vector force scaler product ${displaystyle {vec {F}}_{el}}$ by vector displacement ${displaystyle {vec {dl}}}$ tangent to the trajectory. In addition, the electrical force on the load q is ${displaystyle {vec {F}}_{el}=q{vec {E}}}$ , being ${displaystyle {vec {E}}}$ the electric field due to the Q load. Thus, elementary work ${displaystyle dW}$ you can write:

${displaystyle dW={vec {F}}_{el}cdot {vec {dl}}=F_{e}dlcostheta =F_{e}dr=qEdr}$

being dr is the infinitesimal displacement of the q load in the radial direction from Q and the constant ${displaystyle varepsilon _{0}}$ represents the electric permitivity of the vacuum.

So, work ${displaystyle W}$ due to the electrical force between the Q and q loads can be considered as the one performed by the E electric field created by the Q load to transfer the q load, from one position A to another B, once the electric force has been expressed according to the electric field created by one of them, in this case Q. And it will be, then:

${displaystyle W=int _{A}^{B}{vec {F}}_{el}cdot d{vec {l}}=int _{A}^{B}q{vec {E}}cdot d{vec {l}}=int _{A}^{B}{frac {Qq}{4pi varepsilon _{0}r^{2}}}dr=-leftlbrack {frac {Qq}{4pi varepsilon _{0}r}}rightrbrack _{A}^{B}={frac {Qq}{4pi varepsilon _{0}r_{A}}}-{frac {Qq}{4pi varepsilon _{0}r_{B}}}}$

The work W due to the electrostatic force does not depend on the path followed by the charge q to go from position A to position B, since it only depends on the initial positions ra and final positions rb. This is because the repulsive force Fel, exerted by the source charge Q located at the origin of coordinates on the charge q, is conservative. Moreover, this work done by the electrostatic force is the difference in the values that a function acquires between the starting and finishing positions. This function is precisely the potential energy for the force and the electric field and is written as:

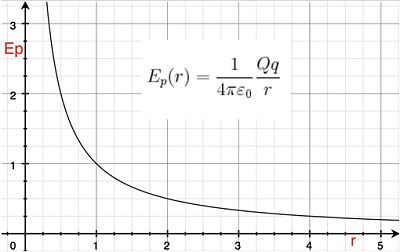
{displaystyle E_{p}(r)={frac {1}{4pi varepsilon _{0}}}{frac {Qq}{r}}}

The electrostatic force that gives rise to the potential energy between the two loads is repulsive if the Q and q loads are of the same sign (as in the case indicated). The potential energy will therefore be a decreasing function with r following the function. ${displaystyle +1/r}$ If the loads were of opposite sign the potential energy would be negative, following the function ${displaystyle +1/r}$ and the attractive electrostatic force. This duality, in the repulsive or attractive character of the electrostatic force and the different sign of the potential energy and potential (by extension), is an intrinsic property to the electrical interaction, which does not possess other fields or forces such as, for example, the gravitation force.

If potential and potential energy functions are used, it is necessary to establish a potential source as a zero-level reference for such functions. Considering punctual loads, the zero value of potential energy is set in the infinite (where potential energy and potential are overturned), that is to ${displaystyle r=infty }$ , ${displaystyle E_{p}=0}$ the potential energy function is defined for all points of space, without the need for any additional constant. Variations of potential energy (or potential) are usually used and, therefore, the work done by the conservation force will not depend on the origin of potentials.

Graphic in which you can check how the value of Ep(r) decreases by increasing the separation between both loads in accordance with the law

{displaystyle {frac {1}{r}}}

To define in a natural way the electric potential from the electrostatic potential energy, consider the potential energy of the charge Q and the charge q= +1 Coul separated by a distance r when the electric field E is created by the source charge Q. In this way, the potential V created by the charge Q will be obtained and which represents, in turn, the potential energy referred to the unit of positive charge. Therefore, it is enough to divide the potential energy, Ep (r) by the charge q, which is located at a distance r from the source charge Q, to obtain the electric potential created by Q at a distance r:

{displaystyle V(r)={frac {E_{p}(r)}{q}}={frac {1}{4pi varepsilon _{0}}}{frac {Q}{r}}qquad qquad [1]}

being the source charge Q at the origin of coordinates. Electric potential has the same behavior with distance r as electric potential energy.

Potential created by a Q punctual load

The fact that the electrostatic force is conservative means that the kinetic energy plus the potential energy associated with the particle with charge q and mass m is a constant, that is, its total energy E remains constant for any position r adopted by the particle inside the region where the field created by Q appears:

{displaystyle E={frac {1}{4pi varepsilon _{0}}}{frac {Qq}{r}}+{frac {mv^{2}}{2}}=constante}

Potential due to a system of point charges

You can calculate the potential at a point P due to the presence of a system of n point charges by superimposing the potential created by each charge, on a given one, independently of the rest. The potential is a scalar magnitude to which the superposition principle can be applied because the equations of electrostatics are linear.

The potential created by a load $q$ at a distance r is given by

{displaystyle V={frac {1}{4pi varepsilon _{0}}}{frac {q}{r}}}

The potential created by multiple loads ${displaystyle q_{1},q_{2},q_{3},...q_{i}}$ in a P point that distan ${displaystyle r_{1},r_{2},r_{3},...r_{i}}$ of each charging center respectively, will be the superposition of the potentials that create each of the loads, separately, at that point

{displaystyle V=V_{1}+V_{2}+V_{3}+...+V_{i}=sum _{i}^{}{frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{r_{i}}}={frac {1}{4pi varepsilon _{0}}}sum _{i}^{}{frac {q_{i}}{r_{i}}}}

The potential due to a continuous charge distribution can be calculated by transforming the last expression. The point charges become infinitesimal charge elements dq and the sum becomes an integral

{displaystyle V={frac {1}{4pi varepsilon _{0}}}int {frac {dq}{r}}}

This expression assumes that V=0 at an infinite distribution distance. It cannot, therefore, be used to obtain the potential created by indefinite charge distributions such as the linear distribution of indefinite charge or the indefinite plane of charge. In every region of space where there is an electric field, there is also an electrostatic potential energy expressible as

{displaystyle E_{p}={frac {varepsilon _{0}}{2}}int {vec {E}}^{2}dVqquad qquad [2]}

extended to the volume of the space where the electric field resides. And being ${displaystyle {vec {E}}^{2}={vec {E}}.{vec {E}}=E^{2}}$ (definition of two vector scaling product).

Equipotential surfaces

A practical way to visualize potential energy or potential in space is to use the graphical representation of equipotential surfaces or surfaces of equal potential. The mathematical definition of equipotential surface applied to potential energy is:

{displaystyle E_{p}=cte}

An equipotential surface represents the locus of all points in space that have the same value of potential and, therefore, the same potential energy. For a point charge, the equipotential surfaces are concentric spheres at the center of which is the charge. On the other hand, field lines are radial and perpendicular to spherical surfaces. For a uniform electric field the equipotential surfaces are planes parallel to each other and perpendicular to the field lines.

If an electric charge that moves along an equipotential surface does not experience changes in potential energy, and therefore in potential. That is to say,

${displaystyle dV={vec {E}}.d{vec {l}}=0}$

Some properties of equipotential surfaces are:

The electric field lines are, at each point, perpendicular to the computer surfaces with sense to the decreasing potentials.
The work to shift a load between two points of the same equipment surface is null.
Two computer surfaces cannot be cut.

When the geometric representation of potentials is done in the plane, equipotential lines appear instead of equipotential surfaces. Now the electric field lines will be perpendicular to the equipotential lines.

1.- Field lines and equipment lines (LE) created by a positive load. The (LE) are circumferences; in three dimensions are spherical surfaces

2.- Field lines and equipment lines (LE) created by a uniform field. The (LE) are straight lines; in three dimensions are planes

3.- Field lines and equipment lines (LE) created by an electric dipole. In three dimensions the (LE) form computer surfaces

Applications

In green, cut off the computer surfaces with a plane perpendicular to the plates of the flat capacitor. Electric field lines in red.

Some applications of potential energy in the field of electrostatics are:

Capacitors

A capacitor is a device that stores energy in the form of electrostatic potential energy inside it. To store the electric charge, which creates the electric field, it uses two conductive surfaces, generally in the form of sheets or plates separated by a dielectric (insulating) material. These boards are what will be electrically charged when connected to a power source. The two plates will be charged with the same amount of charge (q) but with different signs, the magnitude of the charge being proportional to the applied potential difference. The proportionality constant between the charge acquired by the capacitor and the potential difference reached between the two plates is known as the capacitor's capacity:

{displaystyle C={frac {q}{V}}}

Where $q$ is the load of one of the plates and $V$ the difference of potential between them.

A loaded capacitor with a load $q$ and isolated, it represents a system that maintains an electric field $E$ In its interior and therefore, it stores, in the places where the field is present, an electrostatic energy of 'potential' origin. The expression of this electrostatic potential energy can be represented in three equivalent direct forms. In two of them the expression of potential difference appears directly $V$ between his armor:

{displaystyle E_{p}={frac {1}{2}}varepsilon _{0}int E^{2}dV={frac {1}{2}}qV={frac {1}{2}}{frac {q^{2}}{C}}={frac {1}{2}}CV^{2}}

The applications of capacitors are numerous in the field of electronics and, therefore, they are also for consumer appliances. In today's technological applications they are present in multimedia devices such as computers, mobile phones, video and sound players, etc. In these applications of current technology, capacitors are capable of storing electrostatic potential energy for short periods of time and with values that are not excessively high.

The Van de Graaff generator

Van de Graaff Generator Scheme

In 1931 Van de Graaff built the largest electrostatic generator in the world with the purpose of producing a very high potential difference (of the order of 20 million volts) and being able to accelerate charged particles that were made to collide against fixed targets. The results of the collisions allowed information on the characteristics of the atomic nuclei of the material that constitutes the target.

A Van de Graaff generator consists of:

A lower generator that provides positive loads to the Van de Graff device and whose negative pole makes the device's earth paper.
Two pulleys, a bottom equipped with a drive motor, and a top with an insulating material strap adjusted to the two pulleys to transmit the movement of the pulley below the top.
A large hollow cylinder of insulating material containing the mentioned mechanical system.
A large hollow upper metal sphere coupled to the hollow cylinder.
Two very thin metallic wax combs destined to transmit the loads from the lower generator to the hollow metal sphere of the Graaff van device. The first is facing the belt at the lower pulley level and is electrically connected to the positive pole of the lower generator. The second is facing the leash at the top pulley level. The upper metal comb is electrically connected to the inside of the hollow metal sphere.

Operation of the Van de Graff generator

Generator of Van de Graaff de La Casa Mágica, at the St. Louis Children's

The engine that moves the lower pulley is set in motion, drags into the belt and transmits the movement to the upper pulley.
The lower generator provides positive loads to the lower comb. They create a high electric field at the ends of the comb. By the power of the tips of the lower comb, the positive loads are deposited on the outer surface of the pulley.
The loads placed on the belt travel to the top pulley.
The positive loads that reach the height of the upper comb create a high electric field at the tips of the upper comb. By the power of the tips of the upper comb the positive loads of the belt are captured by the comb and carried to the large metal sphere.
The loads pass to the external face of the upper metal sphere.
The process is continuous so that in the upper sphere a huge amount of positive electric charge is accumulated. Between the ground electrode of the lower generator and the upper metal sphere is created a difference of potential of several million volts, which constitutes the objective of the Van de Graff.
If a test dial is connected to the lower ground through a cable and is approaching the upper metal sphere, due to the large potential difference between the two spheres a large electric discharge will occur. Alternatively, in the lower generator you can invest the polarity, putting the positive electrode to the ground and the negative connected to the lower comb. In these conditions the polarities and the loads are reversed: the belt carries the negative loads deposited by the lower comb, the upper comb removes the negative loads of the belt, the upper sphere acquires a great negative load and therefore a very high negative potential regarding the earth.

Applications of the Van de Graaff generator

The large potential difference created by the generator between the upper sphere and the lower earth is used to accelerate charged particles. The charged particles are produced in a source, travel through a vertical accelerator tube, placed not far from the belt, and impact on a sample that acts as a target. Depending on whether one alternative is used, negative ions or positive ions can be accelerated. In summary, the large electrostatic potential energy accumulated in the Van de Graaff, of several million electron-volts (1 electron-volt = 1.6×10⁻¹⁹ J) is used to supply a large kinetic energy to the ions of the particle accelerator. The Van de Graaff generator is also used in Schools and Education Centers to demonstrate the effects of the high electrostatic potential reached in its metallic sphere.

Chemical potential energy

It is a form of potential energy related to the structural organization of atoms or molecules. This organization may be the result of chemical bonds. The chemical energy of a substance can be transformed into other forms of energy through a chemical reaction. For example, when a fuel is burned, chemical energy is converted to heat, in the same way as in the metabolism of food in a biological organism. Photoautotrophic organisms can convert solar energy into chemical energy through a process called photosynthesis, and electrical energy can be converted into chemical energy through electro-chemical reactions (for example, a rechargeable battery).

Nuclear Potential Energy

To be able to unfold in the field of nuclear physics, three observations should be taken into account. The first is that the nucleus of the atom is composed of protons and neutrons and that both together are considered as nucleons, since as such nucleons give the nucleus some of its attributes, for example the existence of the masic number A. The second is that the resolution of the interaction at the particle level should be carried out using the procedures of Quantum Physics, specifically by application of the Schrödinger equation where the expression of the potential energy associated with the phenomenon of interaction is explicitly contained. The third is that to analyze the structure of the nucleus and nucleons it is necessary to move within the margin of distances and dimensions of the femtometers (where ${displaystyle 1fm=10^{-15}m}$ ).

Two types of forces intervene in the structure of the nucleus, the electromagnetic forces associated with the electrical charge of the protons, which are conservative, and the nuclear forces. The latter have some properties that must be known in order to associate the expression of energy with them corresponding potential. The most outstanding characteristics when designing a potential energy for the nucleus can be the following, although there are others:

They are very intense attractive forces so that they exceed in two orders of magnitude the electrostatic repulsion between the protons.
They act equally among nucleons, whether these protons or neutrons.
They are short-range so that a nucleon only interacts with its immediate neighbors.

Of all this it can be deduced that nuclear forces did not just fit into the concept of conservation forces. However, given the usefulness of the potential energy and the need to incorporate it into the Schrödinger equation to solve the problems within the physics at the particle level, the existence of the magnitude can be adopted ${displaystyle E_{p}}$ selecting also the margins of distances where this hypothesis can be feasible by introducing practical models.

For nuclear forces, as for other forces, analytical models, empirical models, graphical models, or mixed models can be built. The basic properties of these and, above all, the proper functioning of the nuclear models when applied to real cases, will determine their acceptance, their rejection or will establish the necessary requirements for their optimization. Each of the models established for the nucleus serves to justify some of its properties. There are no models that encompass a complete description of all nuclear phenomenology.

The Nuclear Potential Barrier

If positively charged particles are released (dotted from a Șzedex load where z represents the number of protons possessing the charged particle) against a sample formed by atoms of atomic number Z (the nuclei of the atoms will possess the load ( ${displaystyle |Ze|}$ ), these will have to overcome a potential barrier to access it. The potential barrier to franking will be of electrostatic origin and will be opposed to the approximation of charged particles.

This potential barrier will be superimposed to the potential energy due to nuclear forces which, in the case of a great approach, will favor the incorporation of the particle into the core to create a new nuclear configuration ${displaystyle ((Z+z)e)}$ . The potential energy model associated with attractive nuclear forces will thus consist of a rectangular well in width ${displaystyle 2R}$ Where $R$ represents the radius of the core, and depth ${displaystyle {-U}_{0}}$ . The barrier model associated with the repulsive electrostatic force will be:

{displaystyle E_{p}(r)={frac {1}{4pi epsilon _{0}}}{frac {|ze||Ze|}{r}}}

Electrostatic energy on the periphery of the radio core ${displaystyle r=R}$ It will fall sharply to ${displaystyle {-U}_{0}}$ when the attractive nuclear forces come into play. Right on the edge of the core the electrostatic barrier will pass by its maximum value:

{displaystyle E_{p}(r)={frac {1}{4pi epsilon _{0}}}{frac {|ze||Ze|}{R}}}

The existence of this barrier implies the need for a contribution of kinetic energy that exceeds the previous value by the impacting charged particle in order to cross it and be incorporated into the nucleus. Particle accelerators will be used to provide kinetic energy to the charged particles ze. However, by virtue of the tunnel effect, some charged particles will be able to cross the potential barrier both in the direction entering the nucleus and in the direction leaving it, without the need for this additional energy contribution. This is the case, for example, of alpha decay.

Nuclear potential energy between two free nucleons

A first hypothesis about the expression of the potential energy between two free nucleons is due to Yukawa:

{displaystyle E_{p}(r)={-E_{0}}r_{0}{frac {e^{^{-r}/_{r_{0}}}}{r}}}

where ${displaystyle r}$ is the distance between the two nucleons in interaction, $r_0$ represents a characteristic distance representative of the "alcance" of the force of nuclear interaction such that

{displaystyle E_{0}=eE_{p}(r_{0})}

This expression, although it can be associated with the action of nuclear forces, suffers from two defects. The first is that since it is a very strong attractive force that increases with the proximity of the nucleons, one would think that it could collapse them. The second, that although neutrons, one of the two classes of nucleon, do not exhibit any electrical charge, protons, the other class of nucleon, possess a unit of elementary electrical charge. These two effects are not taken into consideration, however, in Yukawa's expression.

The first effect was initially analyzed and resolved by Jastrow (1951). For this, he studied the neutron-proton and proton-proton interactions that impacted in the high energy range (of the order of hundreds of MeV). He came to the conclusion of the existence of a repulsive force that arises from a radius somewhat smaller than the radius associated with the nucleon. The repulsive force grows very strongly as the distance between the two interacting nucleons decreases. This lower radius determines the existence of an impenetrable spherical nucleus that protects the integrity of the nucleon, the so-called "hard nucleus". In terms of potential energy, the repulsive force causes a positive potential energy but with a negative slope that decreases very strongly with r and does so with a higher slope in absolute value than that corresponding to the Yukawa potential energy, associated with the nuclear force. attractive.

There are opinions about the size of the "hard core". The radius of a nucleon can be estimated to be rc ≈ 0.7 fm. On the other hand, and according to Thakur, the radius of the "hard core" of a nucleon can be estimated to be rc ≈ 0.4 fm.

The superposition of the two potential energy terms will provide a resulting potential energy curve analogous in qualitative terms to that existing in the interaction between two atoms. Consequently, a potential well will appear that will be characterized by a minimum. Its position will determine the existence of an effective radius of the nucleon and an energy associated with its depth. The composition of these two potential energy terms, the nuclear potential energy and the "hard core", will give rise to a resulting potential energy curve applicable to interactions between two neutrons or between a proton and a neutron.

Potential energy associated with the forces acting between neighboring nucleons. Neutron-proton interaction

The second effect, that is to say the existence of an electromagnetic interaction force, arises from the existence of the positive charges of the nucleus (protons) that will be of a repulsive nature between them, also called Coulomb potential. The latter, therefore, will manifest exclusively between protons but not between neutrons or between neutron and proton pairs. The potential energy corresponding to the electromagnetic interaction between two protons located at the distance r will be

{displaystyle E_{p}(r)={frac {1}{4pi epsilon _{0}}}{frac {e^{2}}{r}}}

and will be incorporated into the contributions provided by the attractive nuclear forces and the repulsive term of Jastrow, to compose the complete expression of the potential energy that arises when studying the interaction between nucleons. In the case of proton-proton interaction, the potential energy of the process will be the superposition of three potential energy components, that due to nuclear forces, that corresponding to the "hard nucleus" and that due to electrostatic repulsion.

Potential energy associated with the forces acting between neighboring nucleons. Proton-proton interaction

Contenido relacionado

Más resultados...

Potential energy

Introduction

Gravitational Potential Energy

Potential energy near the Earth's surface

Escape Velocity

Equipotential surfaces

Examples of Gravitational Potential Energy

Roller Coaster

Pendulum

Application to planetary motion

Elastic potential energy

Hooke's Law

Deduction of elastic potential energy

Properties of the Potential Energy Curve

Electrostatic potential energy and electric potential

Potential due to a system of point charges

Equipotential surfaces

Applications

Capacitors

The Van de Graaff generator

Chemical potential energy

Nuclear Potential Energy

The Nuclear Potential Barrier

Nuclear potential energy between two free nucleons

Contenido relacionado

Longitudinal wave

Riemannian geometry

Picogram