Polygonal number

ImprimirCitar

Polygonal numbers




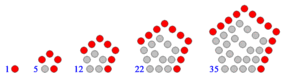
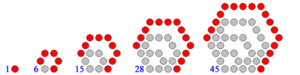
The first four types of polygonal numbers: triangular, quadrangle, pentagonal and hexagonal numbers

In mathematics, a polygonal number is a natural number that can be recomposed into a regular polygon. Ancient mathematicians discovered that numbers could be arranged in certain shapes when represented by stones or seeds.

Polygonal numbers

The number 10 can be recomposed as a triangle (see triangular number):

However, 10 cannot form a square, but 9 can (see square number):

Some numbers, like 36, can be recomposed in both a square and a triangle (see triangular square number):

The method used to enlarge the polygon to the next size is to extend two adjacent arms by one point and then add the required extra sides between the points.

Formulas

A number s-gonal can be broken down s−2 triangular numbers and in a natural number

If $s$ is the number of sides of a polygon, the formula for the $n$ -th number $s$ -gonal $P (s, n)$ is

{displaystyle P(s,n)={frac {(s-2)n^{2}-(s-4)n}{2}}}

{displaystyle P(s,n)=(s-2){frac {n(n-1)}{2}}+n}

The $n$ -th number $s$ -gonal is also related to the triangular $T n$ numbers of the following way:

{displaystyle P(s,n)=(s-2)T_{n-1}+n=(s-3)T_{n-1}+T_{n},.}

Therefore:

{displaystyle {begin{aligned}P(s,n+1)-P(s,n)&=(s-2)n+1,,\P(s+1,n)-P(s,n)&=T_{n-1}={frac {n(n-1)}{2}},.end{aligned}}}

For a given $s$ -gonal number $P (s, n) = x$ , you can find $n$ using the formula

{displaystyle n={frac {{sqrt {8(s-2)x+{(s-4)}^{2}}}+(s-4)}{2(s-2)}}}

and in turn can find $s$ by calculating

{displaystyle s=2+{frac {2}{n}}cdot {frac {x-n}{n-1}}}

Every hexagonal number is also a triangular number

Applying the previous formula:

{displaystyle P(s,n)=(s-2)T_{n-1}+n}

for the 6-sided case, we get:

{displaystyle P(6,n)=4T_{n-1}+n}

but knowing that:

{displaystyle T_{n-1}={frac {n(n-1)}{2}}}

results:

{displaystyle P(6,n)={frac {4n(n-1)}{2}}+n={frac {2n(2n-1)}{2}}=T_{2n-1}}

This shows that the $n$ -'th hex number $P (6, n)$ is also the $(2 n - 1)$ - th triangular number $T 2 n -1$ . The sequence of the hexagonal numbers can be determined simply by taking the odd triangular numbers:

13, 610, 15, 21, 2836, 45, 55, 66...

Nth polygonal number

Yeah. $l$ is the number of sides of a polygon, then the formula for the $n$ - thirtieth polygonal number $l$ sides. ${displaystyle {tfrac {n((l-2)n-(l-4))}{2}}}$ .

Name	Formula	n
Name	Formula	1	2	3	4	5	6	7	8	9	10	11	12	13
Triangular	1⁄2n1n + 1)	1	3	6	10	15	21	28	36	45	55	66	78	91
Square	1⁄2n(22)n - 0)	1	4	9	16	25	36	49	64	81	100	121	144	169
Pentagonal	1⁄2n(3)n - (1)	1	5	12	22	35	51	70	92	117	145	176	210	247
Hexagonal	1⁄2n(4)n - (2)	1	6	15	28	45	66	91	120	153	190	231	276	325
Heptagonal	1⁄2n(5)n - (3)	1	7	18	34	55	81	112	148	189	235	286	342	403
8th	1⁄2n(6)n - (4)	1	8	21	40	65	96	133	176	225	280	341	408	481
Nonagonal	1⁄2n(7)n - (5)	1	9	24	46	75	111	154	204	261	325	396	474	559
Decagonal	1⁄2n(8)n - 6)	1	10	27	52	85	126	175	232	297	370	451	540	637
11-August	1⁄2n(9)n - 7)	1	11	30	58	95	141	196	260	333	415	506	606	715
12-August	1⁄2n(10)n - 8)	1	12	33	64	105	156.	217	288	369	460	561	672	793
13-August	1⁄2n(11)n - 9)	1	13	36	70	115	171	238	316	405	505	616	738	871
14-August	1⁄2n(12)n - 10)	1	14	39	76	125	186	259	344	441	550	671	804	949
15-August	1⁄2n(13)n - 11)	1	15	42	82	135	201	280	372	477	595	726	870	1027
16-August	1⁄2n(14)n - 12)	1	16	45	88	145	216	301	400	513	640	781	936	1105
17-August	1⁄2n(15)n - 13)	1	17	48	94	155	231	322	428	549	685	836	1002	1183
18-August	1⁄2n(16)n - 14)	1	18	51	100	165	246	343	456	585	730	891	1068	1261
19-August	1⁄2n(17)n - 15)	1	19	54	106	175	261	364	484	621	775	946	1134	1339
20-August	1⁄2n(18)n - 16)	1	20	57	112	185.	276	385	512	657	820	1001	1200	1417
21-August	1⁄2n(19)n - 17)	1	21	60	118	195	291	406	540	693	865	1056	1266	1495
22-August	1⁄2n(20)n - 18)	1	22	63	124	205	306	427	568	729	910	1111	1332	1573
23-August	1⁄2n(21)n - 19)	1	23	66	130	215	321	448	596	765	955	1166	1398	1651
24-August	1⁄2n(22)n - 20)	1	24	69	136	225	336	469	624	801	1000	1221	1464	1729
25-August	1⁄2n(23)n - 21)	1	25	72	142	235	351	491	652	837	1045	1276	1530	1807
26-August	1⁄2n(24)n - 22)	1	26	75	148	245	366	511	680	873	1090	1331	1596	1885
27-August	1⁄2n(25)n - 23)	1	27	78	154	255	381	532	708	909	1135	1386	1662	1963
28-August	1⁄2n(26)n - 24)	1	28	81	160	265	396	553	736	945	1180	1441	1728	2041
29-August	1⁄2n(27)n - 25)	1	29	84	166	275	411	574	764	981	1225	1496	1794	2119
30-August	1⁄2n(28)n - 26)	1	30	87	172	285	426	595	792	1017	1270	1551	1860	2197

Properties

The following table includes some properties of the series defined by the polygonal numbers. The results of the sum of the inverses of polygonal numbers are especially relevant. ${displaystyle sum _{i=1}^{infty }{frac {1}{n_{i}}}}$ . The first 6 values in the column "inverse sum", for triangular to octagonal numbers, come from a solution published to the general problem, which also gives a general formula for any number of sides, in terms of the function digomma.

$s$	Name	Formula	Amount of the reverses	Number OEIS
3	Triangular	$1 / 2 (n 2 + n)$	2^{[ ]}	A000217
4	Square	$1 / 2 (22) n 2 - 0 n) = n 2$	π²/6^{[ ]}	A000290
5	Pentagonal	$1 / 2 (3) n 2 - n)$	$3 ln 3 - π \sqrt 3 / 3$ ^{[ ]}	A000326
6	Hexagonal	$1 / 2 (4) n 2 - 2 n) = 2 n 2 - n$	$2 ln 2$ ^{[ ]}	A000384
7	Heptagonal	$1 / 2 (5) n 2 - 3 n)$	${displaystyle {begin{matrix}{tfrac {2}{3}}ln 5\+{tfrac {{1}+{sqrt {5}}}{3}}ln {tfrac {sqrt {10-2{sqrt {5}}}}{2}}\+{tfrac {{1}-{sqrt {5}}}{3}}ln {tfrac {sqrt {10+2{sqrt {5}}}}{2}}\+{tfrac {pi {sqrt {25-10{sqrt {5}}}}}{15}}end{matrix}}}$ ^{[ ]}	A000566
8	8th	$1 / 2 (6) n 2 - 4 n) = 3 n 2 - 2 n$	$3 / 4 ln 3 + π \sqrt 3 / 12$ ^{[ ]}	A000567
9	Nonagonal	$1 / 2 (7) n 2 - 5 n)$		A001106
10	Decagonal	$1 / 2 (8) n 2 - 6 n) = 4 n 2 - 3 n$	$ln 2 + π / 6$	A001107
11	Hendecagonal	$1 / 2 (9) n 2 - 7 n)$		A051682
12	Dodecagonal	$1 / 2 (10) n 2 - 8 n)$		A051624
13	Tridecagonal	$1 / 2 (11) n 2 - 9 n)$		A051865
14	Tetradecagonal	$1 / 2 (12) n 2 - 10 n)$	$2 / 5 ln 2 + 3 / 10 ln 3 + π \sqrt 3 / 10$	A051866
15	Pentadecagonal	$1 / 2 (13) n 2 - 11 n)$		A051867
16	Hexadecagonal	$1 / 2 (14) n 2 - 12 n)$		A051868
17	Heptadecagonal	$1 / 2 (15) n 2 - 13 n)$		A051869
18	Octadecagonal	$1 / 2 (16) n 2 - 14 n)$	$4 / 7 Ln 2 - \sqrt 2 / 14 ln (3 - 2 \sqrt 2)$ $+ π(1 + \sqrt 2) / 14$	A051870
19	Inneadecagonal	$1 / 2 (17) n 2 - 15 n)$		A051871
20	Icosagonal	$1 / 2 (18) n 2 - 16 n)$		A051872
21	Icosihenagonal	$1 / 2 (19) n 2 - 17 n)$		A051873
22	Icosidigonal	$1 / 2 (20) n 2 - 18 n)$		A051874
23	Icositrigonal	$1 / 2 (21) n 2 - 19 n)$		A051875
24	Icositetragonal	$1 / 2 (22) n 2 - 20 n)$		A051876
...	...	...	...	...
10000	Myriagonal	$1 / 2 (9998) n 2 - 9996 n)$		A167149

The OEIS avoids terms that use Greek prefixes (for example, "octagonal") in favor of terms that use numbers (for example, "8-gonal").

A property of this table can be expressed by the following identity (see A086270):

{displaystyle 2,P(s,n)=P(s+k,n)+P(s-k,n),}

with

{displaystyle k=0,1,2,3,...,s-3.}

Multipoly numbers

Some numbers, like 36, which is both square and triangular, belong to two sets of polygonal numbers. The problem of determining, given two sets of this type, all the numbers that belong to both can be solved by reducing the problem to a Pell equation. The simplest example is the sequence of triangular square numbers.

The following table summarizes the set of numbers $s$ -gonal $t$ -gonals for small values of $s$ and $t$ .

$s$	$t$	Sequence	OEIS number
4	3	1, 36, 1225, 41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841860625	A001110
5	3	1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465,...	A014979
5	4	1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801,...	A036353
6	3	All hexagonal numbers are also triangular.	A000384
6	4	1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625, 3338847817559778254844961, 3853027488179473932250054441,...	A046177
6	5	1, 40755, 1533776805,...	A046180
7	3	1, 55, 121771, 5720653, 12625478965, 593128762435, 1309034909945503, 61496776341083161, 135723357520344181225, 63761087640030554511, 14072069153115290487843091,...	A046194
7	4	1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449, 9976444135331412025,...	A036354
7	5	1, 4347, 16701685, 64167869935,...	A048900
7	6	1, 121771, 12625478965,...	A048903
8	3	1, 21, 11781, 203841,...	A046183
8	4	1, 225, 43681, 8473921, 1643897025, 318907548961, 61866420601441, 12001766689130625, 23280871270739841, 451674487259834398561, 87622522247536602581025, 16998317641534841066320321,...	A036428
8	5	1, 176, 1575425, 234631320,...	A046189
8	6	1, 11781, 113123361,...	A046192
8	7	1, 297045, 69010153345,...	A048906
9	3	1, 325, 82621, 20985481,...	A048909
9	4	1, 9, 1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, 5996832038649, 708304623404049, 5385148492712041, 636056763057925561,...	A036411
9	5	1, 651, 180868051,...	A048915
9	6	1, 325, 5330229625,...	A048918
9	7	1, 26884, 542041975,...	A048921
9	8	1, 631125, 286703855361,...	A048924

In some cases, such as $s = 10$ and $t = 4$ , there are no numbers in both sets other than 1.

The problem of finding numbers that belong to three polygon sets is more difficult. A computer search for pentagonal-square triangular numbers has returned only the trivial value of 1, although no proof has yet been found that some number does not exist that might belong to all three classes.

The number 1225 is hecatonicositetragonal ( $s = 124$ ), hexacontagonal ( $s = 60$ ), icosienneagonal ( $s = 29$ ), hexagonal, square and triangular.

The only polygon set that is completely contained in another polygon set is the set of hexagonal numbers, which is contained in the set of triangular numbers.^{[citation needed]}

Contenido relacionado

Más resultados...