Polar coordinates

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Location of a point in polar coordinates

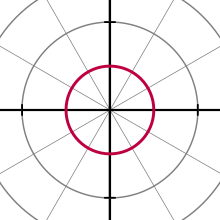
The polar coordinates or polar coordinate system are a two-dimensional coordinate system in which each point in the plane is determined by a distance and an angle. This system is widely used in physics and trigonometry.

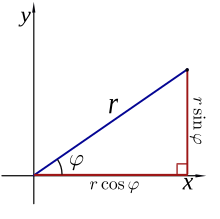
More precisely, the reference system is taken: (a) a point O of the plane, which is called origin or pole; and (b) a directed line (or ray, or segment OL) passing through O, called the polar axis (equivalent to the x of the Cartesian system). With this reference system and a metric measurement unit (to be able to assign distances between each pair of points on the plane), every point P on the plane corresponds to an ordered pair (r, θ) where r is the distance from P to the origin and θ is the angle between the polar axis and the directed line OP which goes from O to P. The value θ increases counterclockwise and decreases clockwise. The distance r (r ≥ 0) is known as the “radial coordinate” or “radius vector”, while the angle is the “angular coordinate” or “polar angle”.

In the case of the origin, O, the value of r is zero, but the value of θ is undefined. Sometimes the convention of representing the origin by (0,0°) is adopted.

History

Polar coordinate system with various angles measured in degrees

Although there are testimonies that the concepts of angle and radius have been known and handled since ancient times, it was not until the XVII century , after the invention of analytical geometry, when one can speak of the formal concept of polar coordinate system.

The first empirical uses of relationships between angles and distances are related to applications to navigation and the study of the celestial vault. The astronomer Hipparchus (190 BC-120 BC) created a trigonometric table that gave the length of a chord as a function of angle. There are also references to the use of polar coordinates to establish the position of the stars. In the treatise On Spirals, Archimedes describes the so-called Archimedean spiral, a function whose radius depends on the angle. However, these applications did not make use of a coordinate system as a means of locating points in the plane, a situation analogous to the state of geometry before the invention of analytic geometry.

In modern times, Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concept of the polar coordinate in the mid-17th centuryXVII in solving geometric problems. Saint-Vincent wrote on this topic in 1625 and published his papers in 1647, while Cavalieri published his writings in 1635 and a corrected version in 1653. Cavalieri first used polar coordinates to solve a problem involving area within a Archimedean spiral. Blaise Pascal later used polar coordinates to calculate the length of parabolic arcs.

However, the abstract concept of a polar coordinate system is due to sir Isaac Newton, who in his Method of Fluxions written in 1671 and published in 1736, introduces eight new coordinate systems (in addition to the Cartesian ones) to solve problems related to tangents and curves, one of which, the seventh, is that of polar coordinates. In the journal Acta Eruditorum Jacob Bernoulli used in 1691 a system with a point on a line, calling them pole and polar axis respectively. The coordinates were determined by the distance to the pole and the angle with respect to the polar axis. Bernoulli's work served as the basis for finding the radius of curvature of certain curves expressed in this coordinate system.

The current term polar coordinates is attributed to Gregorio Fontana, and was used by Italian writers of the XVIII. The term first appears in English in George Peacock's 1816 translation of Sylvestre François Lacroix's Treatise on the Differential and Integral Calculus, while Alexis Clairaut was the first to think of expanding polar coordinates in three dimensions.

Representation of points with polar coordinates

The figure represents a system of polar coordinates on the plane, the reference center (point) O) and the line OL on which the angles are measured. To reference a point indicates the distance to the coordinate center and the angle on the axis OL.

The point (3, 60°) indicates that it is at a distance of 3 units from O, measurements with a 60° angle over OL.
Point (4, 210°) indicates that it is at a distance of 4 units from O and an angle of 210° over OL.

One aspect to consider in polar coordinate systems is that a single point in the plane can be represented with an infinite number of different coordinates, which is not the case in the Cartesian coordinate system. In other words, in the polar coordinate system there is no one-to-one correspondence between the points of the plane and the set of polar coordinates. This occurs for two reasons:

A point, defined by an angle and a distance, is the same point as that indicated by that same angle plus a number of complete revolutions and the same distance. In general, the point ( $r$ , θ) can be represented as ( $r$ , θ ± $n$ ×360°) or (- $r$ θ ± (2 $n$ + 1)180°), where $n$ It's any whole number.
The coordinate center is defined by a null distance, regardless of the angles specified. Arbitrary coordinates (0, θ) are normally used to represent the pole, since regardless of the value taken by the angle θ, a point with radius 0 is always at the pole. These circumstances must be taken into account to avoid confusion in this coordinate system. For a single representation of a point, it is usually limited $r$ to non-negative numbers $r$ ≥ 0 y θ al intervalo [0, 360°] or [−180°, 180°] (in radianes, [0, 2π] or [−π, π]).

Angles in polar notation are usually expressed in degrees or radians, depending on the context. For example, marine navigation applications use degree measurement, while some physical applications (especially rotational mechanics) and most mathematical computation express measurement in radians.

Coordinate conversion

Transition from polar to rectangular coordinates and vice versa

Illustrative diagram of the relationship between the polar coordinates and the Cartesian coordinates

In the xy axle plane with coordinate center at point O you can define a polar coordinate system of a point M of the plane, defined by the distance r to the coordinate center, and the angle $theta$ position vector on axis x.

Conversion from polar to rectangular coordinates

Defined a point in polar coordinates by its angle $theta$ on the x-axis, and its distance r to the coordinate center, you have:

{displaystyle x=rcos theta ,}

{displaystyle y=roperatorname {sen} theta ,}

Conversion from rectangular to polar coordinates

If a point in the plane is defined by its rectangular coordinates (x,y), the polar coordinate r is:

{displaystyle r={sqrt {x^{2}+y^{2}}}}

(applying the Theorem of Pythagoras)

To determine the angular coordinate θ, two cases must be distinguished:

Stop. $r$ = 0, the θ angle can take any real value.
Stop. $r$ ì 0, to obtain a single value of θ, should be limited to an interval of size 2π. By convention, the intervals used are [0, 2π) and (−π, π].

To obtain θ in the interval [0, 2π), the following formulas should be used ( ${displaystyle arctan }$ denotes the reverse of the tangent function:

0{text{ y }}ygeq 0\{frac {pi }{2}}&{text{si }}x=0{text{ y }}y>0\arctan({frac {y}{x}})+pi &{text{si }}x<0\{frac {3pi }{2}}&{text{si }}x=0{text{ y }}y0{text{ y }}yθ θ ={arctan (andx)Yeah.x▪0andand≥ ≥ 0π π 2Yeah.x=0andand▪0arctan (andx)+π π Yeah.x.03π π 2Yeah.x=0andand.0arctan (andx)+2π π Yeah.x▪0andand.0{cHFFFFFF}{cH00FFFF}{cHFFFFFF}{cHFFFFFF}{cH00FF}{cH00FF00}{cH00FF00}{cH00FFFF}{cHFFFFFF}{cH00}{cH00FF}{cH00FFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00FF}{cH00FFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH00FFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00FFFF}{cH00}{cH00FF}{cH00FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{c0{text{ y }}ygeq 0\{frac {pi }{2}}&{text{si }}x=0{text{ y }}y>0\arctan({frac {y}{x}})+pi &{text{si }}x<0\{frac {3pi }{2}}&{text{si }}x=0{text{ y }}y0{text{ y }}y

To get $theta$ in the interval ${displaystyle (-pipi ]}$ , it is considered that ${displaystyle arctan {bigg (}{frac {y}{x}}{bigg)}in {bigg (}-{frac {pi }{2}},{frac {pi }{2}}{bigg)}}$ is a growing function in your domain:

<math alttext="{displaystyle theta ={begin{cases}arctan({frac {y}{x}})-pi &{text{si }}x<0{text{ y }}y<0\-{frac {pi }{2}}&{text{si }}x=0{text{ y }}y0\{frac {pi }{2}}&{text{si }}x=0{text{ y }}y>0\arctan({frac {y}{x}})+pi &{text{si }}xθ θ ={arctan (andx)− − π π Yeah.x.0andand.0− − π π 2Yeah.x=0andand.0arctan (andx)Yeah.x▪0π π 2Yeah.x=0andand▪0arctan (andx)+π π Yeah.x.0andand≥ ≥ 0### #############################################################################################################################################################################################################################################################<img alt="{displaystyle theta ={begin{cases}arctan({frac {y}{x}})-pi &{text{si }}x<0{text{ y }}y<0\-{frac {pi }{2}}&{text{si }}x=0{text{ y }}y0\{frac {pi }{2}}&{text{si }}x=0{text{ y }}y>0\arctan({frac {y}{x}})+pi &{text{si }}x

Many modern programming languages avoid having to store the sign of the numerator and denominator by implementing the atan2 function, which has separate arguments for the numerator and denominator. In languages that allow optional arguments, the atan function can take the x coordinate as a parameter (as in Lisp).

Polar Equations

His name is Polar equation to the equation that defines a curve expressed in polar coordinates. In many cases you can specify such equation by defining $r$ as a function of θ. The resulting curve consists of a series of stitches in the form ( $r$ (θ), θ) and can be represented as the graph of a function $r$ .

Different forms of symmetry of polar function equation can be deducted $r$ . Yeah. $r$ (θ) = $r$ (θ) the curve will be symmetrical regarding the horizontal axis (0°/180°), yes $r$ (180°−θ) = $r$ (θ) will be symmetrical with respect to the vertical axis (90°/ 270°), and $r$ (θ−α°) = $r$ (θ) will be symmetrically α° in the time sense regarding the pole.

Due to the circular nature of the polar coordinate system, many curves can be described with a simple polar equation, whereas in its Cartesian form it would be much more intricate. Some of the best known curves are the polar rose, the Archimedean spiral, the lemniscate, the Pascal spiral and the cardioid.

For the following sections, it is understood that the circle, the line and the polar rose have no restrictions on the domain and range of the curve.

Circumference

A circle with equation

r

(θ) = 1

The general equation for a center circle in ( $r$ ₀, φ) and radio $a$ That's it.

{displaystyle r^{2}-2rr_{0}cos(theta -varphi)+r_{0}^{2}=a^{2}.,}

In certain specific cases, the above equation can be simplified. For example, for a circle with center at the pole and radius a, you get:

{displaystyle r(theta)=a,}

Line

Radial lines (those that cross the pole) are represented by the equation

{displaystyle theta =varphi ,}

where φ is the elevation angle of the line, that is, φ = arctan $m$ where $m$ is the line slope in the cartesian coordinate system. The non radial line crossing the radial line θ = φ perpendicularly to the point ( $r$ ₀, φ) has the equation

{displaystyle r(theta)={r_{0}}sec(theta -varphi).,}

Polar Rose

A polar rose with equation

r

(θ) = 2 without 4θ

The polar rose is a famous mathematical curve that looks like a flower with petals, and can be expressed as a simple polar equation,

{displaystyle r(theta)=acos(ktheta +phi _{0}),}

for any constant ${displaystyle phi _{0}}$ (including 0). Yeah. k is an integer, these equations represent a rose of k petals when k It's odd, or 2k petals if k It's a pair. Yeah. k it is rational but not whole, the graph is similar to a rose but with the flaped petals. Note that these equations never define a rose with 2, 6, 10, 14, etc., petals. The variable a represents the length of the petals of the rose.

If we take only positive values r and values in the interval ${displaystyle [0,2pi),}$ for $theta ,$ , the chart of the equation:

{displaystyle r(theta)=left|asin left({frac {k}{2}}theta +phi _{0}right)right|,}

is a rose of k petals, for any natural number ${displaystyle k,}$ . And yes ${displaystyle k=0,}$ , the graph is a radio circumference ${displaystyle r=|asin(phi _{0})|,}$

Archimedean spiral

An arm of the spiral of Archimedes with equation r(θ) = θ para 0 ك θ ≤ 6π

The Archimedean spiral is a famous spiral discovered by Archimedes, which can also be expressed as a simple polar equation. It is represented by the equation

{displaystyle r(theta)=a+btheta.}

A change to the parameter a will cause the spiral to twist, while b controls the distance between the arms, which is constant for a given spiral. The Archimedean spiral has two arms, one for θ > 0 and another for θ < 0. The two arms are connected at the pole. The mirror image of one arm about the vertical axis produces the other arm. This curve was one of the first curves, after conic sections, to be described in mathematical treatises. It is also the main example of a curve that can be represented most easily with a polar equation.

Other examples of spirals are the logarithmic spiral and the Fermat spiral.

Conic Sections

Elipse, indicting his straight semi-arm

A conic section with one focus at the pole and the other at any point on the horizontal axis (so that the semimajor axis of the conic rests on the polar axis) is given by:

{displaystyle r={ell over {1+ecos theta }}}

where e is eccentricity and $ell$ is the straight semi-layer (the perpendicular distance to a focus from the main axis to the curve). Yeah. e 1, this equation defines a hyperbola; yes e= 1, defines a parable; and e ≤1 defines an ellipse. For the ellipse, the special case e = 0 results in a radius circle $ell$ .

Complex numbers

Illustration of a Complex Number z in the complex plane

Illustration of a complex number in the complex plane using the Euler formula

Each complex number can be represented as a point in the complex plane, and can therefore be expressed as a point in Cartesian coordinates or in polar coordinates. The complex number z can be represented in rectangular form as

{displaystyle z=x+iy,}

where i is the imaginary unit. Alternatively, it can be written in polar form (using the conversion formulas given above) as

{displaystyle z=rcdot (cos theta +ioperatorname {sen} theta)}

so it follows that

{displaystyle z=re^{itheta },}

where e is Neper's constant. This expression is equivalent to the one shown in Euler's formula. (Note that in this formula, as in all those involving angle exponentials, the angle θ is assumed to be expressed in radians.) To go from polar to rectangular form for a given complex number, one can use the conversion formulas seen above.

For multiplication, division, and exponentiation operations on complex numbers, it is usually much simpler to work with complex numbers expressed in polar form than with their rectangular equivalent:

Multiplication:
${displaystyle r_{0}e^{itheta _{0}}cdot r_{1}e^{itheta _{1}}=r_{0}r_{1}e^{i(theta _{0}+theta _{1})},}$
Division:
${displaystyle {frac {r_{0}e^{itheta _{0}}}{r_{1}e^{itheta _{1}}}}={frac {r_{0}}{r_{1}}}e^{i(theta _{0}-theta _{1})},}$
Exponentiation (De Moivre Formula):
${displaystyle (re^{itheta })^{n}=r^{n}e^{intheta },}$

Infinitesimal calculus

Infinitesimal calculus can be applied to equations expressed in polar coordinates. Throughout this section, the angular coordinate θ is expressed in radians, as this is the conventional choice in mathematical analysis.

Differential calculus

Starting from the conversion equations between rectangular and polar coordinates, and taking partial derivatives, we obtain

{displaystyle r{tfrac {partial }{partial r}}=x{tfrac {partial }{partial x}}+y{tfrac {partial }{partial y}},}

{displaystyle {tfrac {partial }{partial theta }}=-y{tfrac {partial }{partial x}}+x{tfrac {partial }{partial y}}.}

To find the slope in Cartesians of the tangent line to a polar curve r(θ) at a given point, the curve must first be expressed as a system of parametric equations

{displaystyle x=r(theta)cos theta ,}

{displaystyle y=r(theta)operatorname {sen} theta ,}

Differentiating both equations with respect to θ results

{displaystyle {frac {dx}{dtheta }}=r'(theta)cos theta -r(theta)operatorname {sen} theta ,}

{displaystyle {frac {dy}{dtheta }}=r'(theta)operatorname {sen} theta +r(theta)cos theta.,}

Dividing the second equation by the first gives the Cartesian slope of the tangent line to the curve at the point (r, r(θ)):

{displaystyle {frac {dy}{dx}}={frac {r'(theta)operatorname {sen} theta +r(theta)cos theta }{r'(theta)cos theta -r(theta)operatorname {sen} theta }}.}

Integral calculus

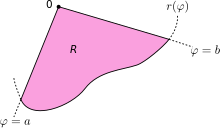
The region R is bound by the curve r(θ) and semirrectas θ = a and θ = b.

Let R be a region of the plane bounded by the continuous curve r(θ) and the rays θ = a and θ = b, where 0 < b − a < 2π. Then, the area of R is given by

{displaystyle S={frac {1}{2}}int _{a}^{b}r(theta)^{2},dtheta.}

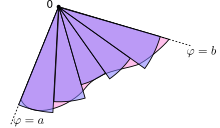
The region R approaching n sectors (here, n = 5).

This result can be obtained as follows. First, the interval [a,b] is divided into n subintervate them, where n It's any positive integer. Therefore Δθ, the length of each subinterval, is equal to b−a (the total length of the interval) divided by n (the number of sub-intervals). For each sub-interval i = 1, 2,..., n, be θ_i his midpoint. You can build a circular sector with center at the pole, radio r(θ_i), central angle Δθ and arc length ${displaystyle r(theta _{i})Delta theta ,}$ . The area of each sector is then equal to

{displaystyle S_{i}={tfrac {1}{2}}r(theta _{i})^{2}Delta theta }

Therefore, the total area of all sectors is

{displaystyle S_{n}=sum _{i=1}^{n}S_{i}=sum _{i=1}^{n}{tfrac {1}{2}}r(theta _{i})^{2},Delta theta.}

The larger n is, the better the approximation to the area. In the limit, when n → ∞, the sum becomes a Riemann sum, and thus converges on the integral

{displaystyle lim _{nto +infty }S_{n}={frac {1}{2}}int _{a}^{b}r(theta)^{2}mathrm {d} theta =S}

Generalization

Using Cartesian coordinates, an infinitesimal area element can be computed as dA = dx dy. The method of integration by substitution for multiple integrals states that when another coordinate system is used, the Jacobian conversion matrix must be taken into account:

{displaystyle J=det {frac {partial (x,y)}{partial (r,theta)}}={begin{vmatrix}{frac {partial x}{partial r}}&{frac {partial x}{partial theta }}\{frac {partial y}{partial r}}&{frac {partial y}{partial theta }}end{vmatrix}}={begin{vmatrix}cos theta &-roperatorname {sen} theta \operatorname {sen} theta &rcos theta end{vmatrix}}=rcos ^{2}theta +roperatorname {sen} ^{2}theta =r.}

Therefore, an element of area in polar coordinates can be written as:

{displaystyle dA=J,dr,dtheta =r,dr,dtheta.}

A function in polar coordinates can be integrated as follows:

{displaystyle iint _{R}f(r,theta),dA=int _{a}^{b}int _{0}^{r(theta)}f(r,theta),r,dr,dtheta.}

where R is the region enclosed by a curve r(θ) and the lines θ = a and θ = b .

The formula for the area R mentioned above is obtained by taking f as a constant function equal to 1. One of the applications of these formulas is the calculation of the Integral de Gauss: ${displaystyle int _{-infty }^{infty }e^{-x^{2}},dx={sqrt {pi }}.}$

Vector calculus

The vector calculation can also be applied to the polar coordinates. Sea ${mathbf {r}}$ position vector ${displaystyle (rcos thetaroperatorname {sen} theta),}$ , with r and $theta$ dependent on time t.

Let

{displaystyle {hat {mathbf {r} }}=(cos thetaoperatorname {sen} theta)}

a unit vector in the direction of ${mathbf {r}}$ and

{displaystyle {hat {boldsymbol {theta }}}=(-operatorname {sen} thetacos theta)}

an orthogonal unit vector ${mathbf {r}}$ . The first and second derivatives of the position vector are:

{displaystyle {frac {dmathbf {r} }{dt}}={dot {r}}{hat {mathbf {r} }}+r{dot {theta }}{hat {boldsymbol {theta }}},}

{displaystyle {frac {d^{2}mathbf {r} }{dt^{2}}}=({ddot {r}}-r{dot {theta }}^{2}){hat {mathbf {r} }}+(r{ddot {theta }}+2{dot {r}}{dot {theta }}){hat {boldsymbol {theta }}}=({ddot {r}}-r{dot {theta }}^{2}){hat {mathbf {r} }}+{frac {1}{r}}quad {dot {overbrace {r^{2}{dot {theta }}} }}quad {hat {boldsymbol {theta }}}}

Extension to more than two dimensions

Three dimensions

The polar coordinate system can be extended to three dimensions with two different coordinate systems: the cylindrical coordinate system and the spherical coordinate system. The cylindrical coordinate system adds a distance coordinate, while the spherical coordinate system adds an angular coordinate.

Cylindrical coordinates

A point represented in cylindrical coordinates

Main article: Cylindrical coordinates

The cylindrical coordinate system is a coordinate system that extends the polar coordinate system by adding a third coordinate that measures the height of a point on the plane, in the same way as the Cartesian coordinates extends to three dimensions. The third coordinate is usually represented by h, making the notation for those coordinates (r, θ, h).

Cylindrical coordinates can be converted to Cartesian coordinates as follows:

{displaystyle {begin{aligned}x&=r,cos theta \y&=r,operatorname {sen} theta \z&=h.end{aligned}}}

Spherical coordinates

A point represented in spherical coordinates

Main article: Spherical coordinates

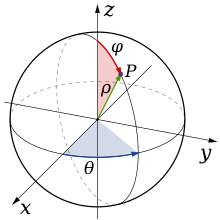
Polar coordinates can also be extended to three dimensions using the coordinates (ρ, φ, θ), where ρ is the distance to the origin, φ is the angle with respect to the z-axis (measured from 0° to 180°), and θ is the angle with respect to the x-axis (same as in polar coordinates, between 0° and 360°). This coordinate system is similar to the system used to denote the altitude and latitude of a point on the Earth's surface, where the origin is located at the center of the Earth, the latitude δ being the complementary angle of φ (i.e., δ = 90° − φ), and the longitude l is given by θ − 180°.

Spherical coordinates can be converted to Cartesian coordinates as follows:

{displaystyle {begin{aligned}x&=rho operatorname {sen} phi cos theta \y&=rho operatorname {sen} phi operatorname {sen} theta \z&=rho cos phi end{aligned}}}

Polar coordinates in space are of special interest when the angles determine the function, as in the case of the helix.

N dimensions

It is possible to generalize these extensions in such a way that a representation system for 4 or more dimensions is obtained. For example, for 4 dimensions you get

{displaystyle {begin{aligned}x&=rho operatorname {sen} gamma operatorname {sen} phi cos theta \y&=rho operatorname {sen} gamma operatorname {sen} phi operatorname {sen} theta \z&=rho operatorname {sen} gamma cos phi \t&=rho cos gamma end{aligned}}}

Applications

Polar coordinates are two-dimensional, so they can only be used where the positions of points lie on a two-dimensional plane. They are the most appropriate in any context where the phenomenon to be considered is directly linked to the direction and longitude of a central point, such as figures of revolution, rotating movements, stellar observations, etc. The examples seen above show how easily polar coordinates define curves like the Archimedean spiral, whose equation in Cartesian coordinates would be much more intricate. Furthermore, many physical systems, such as those related to bodies moving around a central point, or phenomena originating from a central point, are simpler and more intuitive to model using polar coordinates. The initial motivation for the introduction of the polar system was the study of circular motion and orbital motion.

Position and navigation

Polar coordinates are often used in navigation, since the destination or direction of travel can be given by an angle and a distance to the object under consideration. Aircraft, for example, use a slightly modified polar coordinate system for navigation.

Modeling

The systems that represent radial symmetry have characteristics suitable for the polar coordinate system, with the central point acting as the pole. A prime example of this use is the groundwater flow equation when applied to radially symmetric wells. In the same way, systems influenced by a central force are also good candidates for the use of polar coordinates. Some examples are radio antennas, or gravitational fields, which obey the inverse square law (see the two-body problem).

Radially asymmetric systems can also be modeled with polar coordinates. For example, the directivity of a microphone, which characterizes the sensitivity of the microphone as a function of the direction of the received sound, can be represented by polar curves. The curve of a standard cardioid microphone, the most common of microphones, has the equation r = 0.5 + 0.5 sin θ.

Scalar Fields

A problem in the mathematical analysis of functions of several variables is the difficulty in proving the existence of a limit, since different results can be obtained depending on the path of approach to the point. At the origin of coordinates, one of the most interesting points for analysis (for usually canceling rational or logarithmic functions), this problem can be solved by applying polar coordinates. At other points it is possible to change the reference system and thus apply the trick.

By substituting the Cartesian coordinates x, y, z, …, by their corresponding equivalences in polar coordinates, the limit when approaching the origin is reduced to a limit of a single variable, which is easy to calculate since it is the sine and the cosine bounded functions and r an infinitesimal. If the result does not show angular dependence, it is possible to assert that the limit is indistinct from the point and trajectory from which it has been approached.

Contenido relacionado

Más resultados...