Planck's constant
| Value h | Units |
|---|---|
| 6,626 070 15 × 10- 34 | J⋅s |
| 4,135 667 696 × 10-15 | eV⋅s |
| Value (h-barra) | Units |
| 1,054 571 817 × 10- 34 | J⋅s |
| 6,582 119 569 × 10-16 | eV⋅s |
| Value hc | Units |
| 1,986 445 86 × 10-25 | J⋅m |
| 1,239 841 93 | eV⋅μm |
| Value )c (h-barra) | Units |
| 3,161 526 49 × 10-26 | J⋅m |
| 0.197 326 9804 | eV⋅μm |
La Planck constant It is a physical constant that plays a central role in the theory of quantum mechanics and receives its name from its discoverer, the German physicist and mathematician Max Planck, one of the parents of that theory. Denoted as h{displaystyle h}, is the constant that is often defined as the elemental act. Planck would call it precisely “when much action” (in German, Wirkungsquantum), because the amount called action of a physical process (the product of the energy involved and the time used) could only take discrete values, that is, whole multiples of the energy involved h{displaystyle h}.
It was initially proposed as the constant proportionality between energy E{displaystyle E} of a photon and frequency f{displaystyle f} of its associated electromagnetic wave.
- E=hf{displaystyle E=hf,}
Since the frequency f{displaystyle f}, wavelength λ λ {displaystyle lambda }and the speed of light c{displaystyle c} meet λ λ f=c{displaystyle lambda f=c} can be expressed as:
- E=hcλ λ {displaystyle E={frac {hc}{lambda }},}
Another fundamental equation involving Planck's constant is the one that relates the linear moment p{displaystyle p} of a particle with the wavelength of De Broglie λ of the same:
- λ λ =hp{displaystyle lambda ={frac {h}{p}}}}
In applications where frequency is expressed in radian terms per second or angular frequency, it is useful to include the factor 12π π {displaystyle {frac {1}{2pi}}}} within Planck's constant. The resulting constant, "constant of Planck reduced" or "constant of Dirac", is expressed as ("h":
- =h2π π {displaystyle hbar ={frac {h}{2pi }}}}
This way the energy of a photon often angular ω ω {displaystyle omega }Where ω ω =2π π f{displaystyle omega =2pi f}can be expressed as:
- E= ω ω {displaystyle E=hbar omega }
On the other hand, the reduced Planck constant is that of the angular moment in quantum mechanics. The values that can take the orbital, spin or total angular moment are whole or semi-entered multiples of the reduced constant. Yeah. J{displaystyle J,} is the total angular moment of a system with rotational invariance and Jz{displaystyle J_{z},} is the angular moment of the system measured on any direction, for example the z axis, these amounts can only take the values:
- J2=j(j+1) 2j=0,1/2,1,3/2,...... Jz=m ,m=− − j,− − j+1,...... ,j{displaystyle {begin{matrix}J^{2}=j(j+1)hbar ^{2} fakej=0,1/2,1,3/2,ldots \J_{z}=mhbarqquad quad &m=-j,-j+1,ldotsjend{matrix}}}}}}}.
Unicode reserves the codes U+210E (h) for Planck's constant and U+210F (h with slash) for Dirac's constant.
Source of constant
History
The path that led Max Planck to his constant had its origins in a project that began a quarter of a century earlier, the theory of "the law of energy distribution of the normal spectrum". In it he studied radiation heat emitted by a body due to its temperature. In this theory, the concept of a black body was introduced in 1862, whose surface absorbs all the thermal radiation that falls on it and which also emits thermal radiation with the same spectrum at the same temperature.
However, an experimental study of the black body led to a discrepancy between the experimental results and those obtained by applying the laws of classical Physics. According to the Stefan-Boltzmann law, the spectral radiance of bodies increases rapidly with the fourth power of temperature and also moves towards higher frequencies (Wien's displacement law). The problem arose when calculating the energy absorbed by the black body at a given temperature using the energy equipartition theorem, since as the frequency increased the theoretical prediction tended to infinity while experiments showed that the energy density is always finite and tends to zero for very high frequencies. This unrealistic behavior of classical theories at high frequencies is known as «ultraviolet catastrophe». Planck was interested in making sense of this dilemma; To achieve this, he decided to consider the energy absorbed and emitted by the black body in the form of discrete "packets." By carrying out the calculations according to this procedure, and through numerical work, he obtained a good agreement between the experimental and theoretical results, introducing a constant that later became known as Planck's constant (h).
Planck's work marked the beginning of quantum mechanics (QM), which brought with it a change of mentality in the way of understanding natural phenomena on an atomic scale. The next step came from the hand of Albert Einstein who, in a similar way to Planck, raised the absorption of light by a metal in a discrete way, to quanta, and its corresponding emission of electrons, in the photoelectric effect. Another step taken at the beginning of the XX century was the one obtained with Bohr's model of the atom and his postulates, revolutionizing the concept of the atom; this new concept of the emission and absorption of light by matter intervenes in a discreet way. Finally, there is also a relationship between Planck's theory and his constant with Heisenberg's uncertainty principle.
Order of magnitude of the constant
When the value of Planck's constant is expressed in SI units, the resulting value is very small, approximately 6.63 x 10-34 J s, indicating that it does not seem applicable to a scale adapted to humans (where the usual values are meters, kg or seconds). Planck's constant is applied in physics when working on an atomic scale; for example, when calculating the energy of a photon of the visible spectrum in green with a frequency of 5.77 x 1014 Hz. each photon of this frequency has an energy of h.f = 3.82x 10 -19 J. To apply Planck's constant at a macroscopic level, it would be necessary to do it with amounts of photons proper to our scale. In this case it can be compared, for example, with a mole of photons (NA = 6.02x1023 molec/mol). If we apply Planck's constant not to a photon but to a hypothetical quantity of one mole of photons, the resulting energy is of the order of 230 kJ/mol, which is already a typical measurement in everyday life, which makes clear the different scales on which nature can be valued: the atomic (on the order of, for example, Planck's constant), the human (applying the SI base units), or the universe (on the order of, for example, the speed of light that allows distances to be measured in light years).
Blackbody radiation
Definition of blackbody
The name black body was introduced by Gustav Kirchhoff in 1862 and his idea derives from the following observation: all matter emits electromagnetic radiation when it is at a temperature above absolute zero. The electromagnetic radiation emitted by a body at a given temperature is a spontaneous process and comes from a conversion of its thermal energy into electromagnetic energy. It also happens the other way around, all matter absorbs electromagnetic radiation from its environment as a function of its temperature. An object that absorbs all the radiation incident on it at all frequencies is called a black body. When a black body has a uniform temperature, the radiation it emits presents a distribution as a function of frequency (or wavelength, inversely related to it) that is characteristic and depends on its temperature. The surface of a star like our Sun has a temperature of 5800 Kelvin and emits radiation with a maximum that is about 500 nm (visible light). On the other hand, the human body, whose average temperature is much lower, is around 37 degrees Celsius, and therefore emits its maximum at longer wavelengths, around 10 micrometers, which corresponds to infrared.
This radiation is known as black body radiation. The concept of a black body is an idealization since a perfect black body does not exist in nature. An ideal black body is considered to be one that absorbs all the radiation that reaches it without reflecting it in such a way that it only emits that corresponding to its temperature.
Preliminary ideas
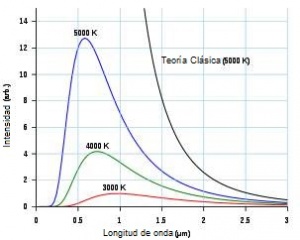
By the late 19th century classical physics could provide explanations for most observed phenomena. However, some physicists noticed certain relative mismatches in the atomic emission and absorption spectra in the range of wavelengths in the visible spectrum or in the decrease with temperature of the molar heat of solids that did not explain the Dulong and Petit's law. The biggest mismatch in classical theory is known as "the ultraviolet catastrophe" or Rayleigh-Jeans and is related to the emission of radiation by bodies in thermal equilibrium at a given temperature. According to the law enunciated by Rayleigh and Jeans, the energy density emitted by a black body for each frequency and temperature was proportional to the square of the frequency, which implied that the higher the frequency, the greater the amount of energy supplied. by the body Therefore, the most important contribution to the energy density of the radiation emission from the black body corresponds to the radiation of shorter wavelength (higher frequency), which in the limit of the visible corresponds to ultraviolet radiation.
However, experimental measurements show the opposite, that is, that the emission of radiation decreases with decreasing wavelength (with increasing frequency), tending to zero in the ultraviolet region. Furthermore, if the total energy emitted by the black body is calculated for all wavelengths at a high temperature like that of a star, the classical law would give an infinite energy; a star does not emit infinite radiation and this result violates the law of conservation of energy, thus calling into question the classical law or Rayleigh-Jeans law.
It was Max Planck who proposed the law that bears his name and which, through the idea of emission and absorption of light by matter in a discrete manner at "quanta" of energy h f, solves the problem of emission and absorption of radiation by bodies in thermal equilibrium at a given temperature. This way of approaching the problem of the emission and absorption of electromagnetic energy created a new conception of the physical world.
Late 19th century and early XX it was virtually impossible to realize that the root of the problems presented by the interpretation of some physical phenomena lay in the assumption that energy was continuous. This change of mentality that supposes the emission and absorption of light by bodies in the form of quanta of energy would also be revealed by Einstein in 1905 with the explanation of the photoelectric effect.
Planck's law for black body emission
Planck's law establishes that the electromagnetic energy absorbed or emitted by a black body is carried out through the exchange of quanta of electromagnetic energy hf, according to the following expression,
I(f,T)=2f2c2hfehf/kT− − 1{displaystyle I(f,T)={frac {2f^{2}}{c^{2}}}{frac {hf}{e^{hf/kT}-1}}}{qquad }
where:
- I (f,T) is the energy per time unit (or the power), per surface area unit that emits in the normal direction, by solid angle unit, and by frequency unit, radiated by a black body at temperature T;
- h is the constant of Planck;
- c is the speed of light in the void;
- k is the Boltzmann constant;
- f is the frequency of electromagnetic radiation and
- T is the body temperature in Kelvin.
You can see how it appears reflected in the exponential term of this distribution function I(f,T){displaystyle I(f,T)} the energy ratio hf. Planck's law behaves properly in experimental measurements of astrophysics, and more directly related to the Earth, in those applications where the solar spectrum intervenes for the entire frequency margin of the electromagnetic spectrum.
After a few years, the success of his quantum theory for the correct interpretation of entropy and the third law of thermodynamics, as well as Einstein's ideas on the quantum theory of radiation, reaffirmed Planck in the certainty of his theory.
Verification: Rayleigh-Jeans law
In the classical limit of low frequencies, Planck's law coincides with the Rayleigh-Jeans law:
I(f,T)=2f2c2hfehf/kT− − 1=2f2c2hf(1+hfkT+...)− − 1≈ ≈ 2f2c2kT{displaystyle I(f,T)={frac {2f^{2}}{c^{2}}}{efrac {hf}{e^{hf/kt}-1}}{frac}{2f^{2}}{c}{c^{2}}{c⁄2}}}{cf}{cf}{x1⁄2f}}{cf}}{cf}}{cf}{cf}{cf}{cf}{cf}{cf}{cf}}{cf}{cf}{cf}{cf}{cf}{cd}{cd}{cf}}}}{cf}{cd}{cf}{cf}{cf}{cf}{cf}{cd}{cd}{cd}{cf}{cf}{cf
For intermediate and high frequencies, however, they differ. Furthermore, as the frequency f increases, the second increases indefinitely while the first tends to zero.
The photoelectric effect
In 1887 Heinrich Rudolf Hertz discovered that an electric discharge between two electrodes occurred more easily when ultraviolet light fell on one of them. Subsequently, Philipp Lenard demonstrated that ultraviolet light facilitates electrical discharge since it causes the emission of electrons from the cathode surface. However, Albert Einstein earned this experiment to contradict some aspects of classical electromagnetic theory, and its correct interpretation earned him the Nobel Prize in 1921. The photoelectric effect has been one of the most interesting examples to illustrate the corpuscular nature of light, leading to the development of quantum mechanics during the 20th century.
When light of a certain wavelength falls on the surface of a metal, it emits a flow of electrons. At the time this discovery was made, the wave theory of light was the only model available. According to this, the number of emitted electrons should increase proportionally to the intensity of the light; In addition, there should be a time margin between the incidence of the photons and the emission of the electrons. When proceeding to the experimentation, none of these conditions turned out to be true. The luminous intensity does not affect the emission of the electrons, but it does affect the frequency, since the photoelectric effect only occurs for certain values of this and the time frame is irrelevant. The wave theory, therefore, is not valid when explaining the photoelectric effect.
To justify the phenomenon, Einstein used an idea proposed by Max Planck in 1900 to explain a similar paradox that arose when interpreting blackbody radiation. Planck considered light as a series of discrete packets which he called quanta rather than as a wave. Using this theory, Einstein determined that the energy of the quanta, particles that we call photons, is related to the frequency of the light wave through the expression:
E=hf{displaystyle E=hf}
Where E{displaystyle E} is the kinetic energy of the photon, f{displaystyle f} frequency and h{displaystyle h} the constant of Planck (6,63↓ ↓ 10− − 34J.s){displaystyle (6,63*10^{-34}J.s)} Once the energy of the photon is established, the photoelectric effect becomes a simple case of application of the principle of energy conservation.
When the light incites on a surface, it is providing some energy, E{displaystyle E}particularly the electrons on the surface. There is a specific energy value needed to “take off” the electron, called threshold energy and also work function,≈ ≈ u{displaystyle Phi _{u}}. The excess of energy above ≈ ≈ u{displaystyle Phi _{u}} will appear in the form of kinetic energy of the electron,Ec{displaystyle E_{c}}which will acquire the speed corresponding to the aforementioned kinetic energy.
E(fortorn)=≈ ≈ u+Ec(electrorn){displaystyle E(foton)=Phi _{u}+E_{c}(electron)}There are several procedures to verify this equation. One is to measure the potential differences between electrodes of a photoelectric cell with a voltmeter by illuminating the cell with monochromatic light of various wavelengths. As a result, different potential differences will be created V{displaystyle V} between electrodes and there will appear a current step produced by electrons removed from the cathode. A variation of this experiment would consist of connecting the cell to a battery with the reversed polarities and adjusting the value of it until the current of the cell descended to zero, which would mean that the opposite field created is able to prevent the electrons from getting off the metal surface. Both methods must verify the principle of energy conservation and therefore must fulfill that the kinetic energy of the emitted electrons comes from the difference of potential V{displaystyle V} between the electrodes of the photocell in the first case and in the second represents the potential V{displaystyle V} opposite that is applied and that cancels the established current. Therefore, the equation can be written as follows:
qV=hf− − ≈ ≈ u{displaystyle qV=hf-Phi _{u}}Where q{displaystyle q} is the load of the electron and V{displaystyle V} the braking potential.
The solution that Einstein proposed to the problem of the photoelectric effect completely solves the inconveniences of the wave model. By treating light as quanta, it can be understood that the intensity of the light does not affect the energy of the electron, but the number of electrons that are emitted, all of them with the same energy, which depends on the frequency. For the same reason, this effect is not seen for all frequencies, but only when the photon has enough energy to exceed the threshold energy. Finally, there is no reason for there to be a time frame to appreciate the effect, since the electron is released as soon as the photon hits the surface. This fact constitutes definitive proof of the corpuscular nature of light.
Atomic models: the Bohr atomic model
Niels Bohr was a Danish physicist who contributed to the understanding of the structure of the atom and quantum mechanics. Based on Ernest Rutherford's theories, he published his atomic model in 1913, in which he introduced the theory of quantized orbits, and in 1922 received the Nobel Prize in Physics for his work on atomic structure and radiation. Numerous physicists, based on this principle, concluded that light had a wave-particle duality.
In atomic physics, the Bohr model of the atom presents the atom as a small positively charged nucleus surrounded by electrons that move around the nucleus in circular orbits, similar in structure to the solar system, but with an attraction produced by electrostatic forces instead of gravity. It was an improvement over the previous Thomson model or the Rutherford model. Since the Bohr model is a modification of the Rutherford model based on quantum physics, different sources combine the two and speak of the Rutherford-Bohr model.[citation needed] The key to the success of the model lies in explaining Rydberg's formula for the spectral emission lines of atomic hydrogen. Rydberg's formula worked experimentally but could not be justified theoretically until Bohr introduced his model. This not only explains the reason for the structure of Rydberg's formula, but also provides a justification for his empirical results in terms of fundamental physical constants. Compared to the current model theory, the Bohr model is a primitive model of the hydrogen atom but, due to its simplicity and its correct results in the interpretation of some concrete systems, the Bohr model always appears in introductions to mechanics. quantum.[citation needed]
Bohr's contributions to his model of the atom are contained in the second and third postulates. In the second, he establishes the quantization condition of the orbits of the electrons in the atom and in the third, he introduces the hypothesis that the energy of an electron in the atom can only be exchanged with the environment, in small amounts that are a multiple of Planck's constant., passing from one orbit to another according to the condition of the second postulate. The third postulate prevents, among other things, the electron in its movement around the nucleus from continuously losing energy and being thrown towards the nucleus as predicted by classical theory.
First Postulate
Electrons move in certain permitted circular orbits around the nucleus without emitting energy. In the atom there is no emission of electromagnetic radiation while the electron remains in its orbit. The reason why the electron does not radiate energy is a postulate, since according to classical electrodynamics a charge in accelerated movement, such as rotation, must emit energy in the form of radiation.
To obtain the energy of the electron in a given orbit as a function of its radius, Bohr assumes circular orbits and uses the following reasoning: the rotational movement of the electron is maintained by the action of the attractive Coulomb force due to the presence of the positive nucleus. This force is precisely the centripetal force necessary to keep the electron in its circular orbit. This leads to the following expression:
kZe2r2=mev2r{displaystyle k{Ze^{2} over r^{2}}}={m_{ev^{2} over r}}}
Where the first term is the strength of Coulomb and the second is the centripetal force; k is the constant of the strength of Coulomb, Z It's the atomic number, e is the charge of the electron, me{displaystyle m_{e} is the mass of the electron, v is the speed of the electron in the orbit and r the orbit radius.
Starting from the previous equation and knowing that the total energy is the sum of the kinetic and potential energies, the energy of an electron is expressed as a function of the radius r of the orbit as:
E=− − 12kZe2r{displaystyle E=-{1over 2}{kZe^{2} over r}}
With this postulate, Bohr avoided the problem of the orbital instability of the electron, and therefore of the atom, predicted by classical electrodynamics. It does this by postulating that the radiation of energy by charged particles is valid on the macroscopic scale, but not applicable to the microscopic world of the atom. However, the problem of explaining the transition between stationary states and the emission of radiation by the atom arose, for which Bohr introduced another postulate.
Second Postulate
The quantification condition of the orbits allowed for the movement of the electron in the atom is one of the great contributions of Bohr, although it does not appear in its first postulate. Bohr makes use of the Planck constant as an elementary angular moment so that the possible angular moments of the electron are only the entire multiples of the aforementioned elementary angular moment.[chuckles]required] Thus, not all the orbits of the electron around the nucleus are allowed, only those whose radius meets the angular moment, L{displaystyle L}the electron is an integer multiple =h2π π {displaystyle hbar ={h over 2pi }}.
From this, the quantization condition remains for the radii allowed for the electron are:
rn=n2 2kmeZe2{displaystyle r_{n}={n^{2}hbar ^{2} over km_{e}Ze^{2}}}
With n=1,2,3,...... {displaystyle n=1,2,3,dots };
Replace permitted radios rn{displaystyle r_{n}} in the expression of energy the energy corresponding to each permitted orbit can be obtained:
En=− − 12k2mZ2e4n2 2{displaystyle E_{n}=-{1 over 2}{k^{2}mZ^{2}{2}{}{4 over n^{2}hbar ^{2}}}}}}}
Third Postulate
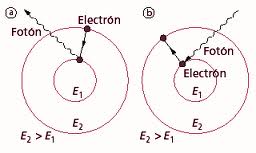
The electron only emits or absorbs energy in the jumps from one allowed orbit to another. In this change it emits or absorbs a photon whose energy is the difference of energy between both levels. The photon, following Planck's ideas, has an energy:
Eγ γ =h.. =Eni− − Enf{displaystyle E_{gamma }=hnu =E_{n_{i}}-E_{n_{f}}}}
Where ni{displaystyle n_{i}} identify the initial orbit and nf{displaystyle n_{f}} the end, and .. {displaystyle nu } It's the frequency of the photon. Introducing the values of the energies associated with each orbit is obtained for the frequency of the emitted or absorbed photon:
.. =k2meZ2e42h 2(1nf2− − 1ni2){displaystyle nu ={k^{2}m_{e}Z^{2}e^{4 over 2hhbar ^{2}}left({1 over n_{f}{2}}{2}}}-{1 over n_{i}{2}}{2}}{2}}}{1right)}}
This last expression derived from quantum principles confirms the empirical formula found earlier by Balmer and commonly used by spectroscopists to describe the Balmer Series —observed since the turn of the century XIX— in the de-excitation of Hydrogen and which was given by:
.. ! ! =1λ λ =RH(122− − 1n2){displaystyle {overline {nu }}={1 over lambda }=R_{H}left({1 over 2^{2}}}-{1 over n^{2}}}{right)}}
With n=3,4,5,...... {displaystyle n=3,4,5,dots } and where RH{displaystyle R_{H}} is Rydberg's constant call for hydrogen. The experimentally measured value of Rydberg's constant (1,097107m− − 1){displaystyle (1,09710^{7}m^{-1}}}It matches the value of Bohr's theoretical formula.
Bohr's postulates correspond to a first consideration of the fact that the stable electrons orbiting in an atom are described by stationary wave functions.
Heisenberg's uncertainty principle
Introduction
Werner Heisenberg —Nobel Prize Winner in Physics in 1932— enunciated the so-called uncertainty principle or indeterminacy principle, according to which it is impossible to measure simultaneously, and with absolute precision, the value of the position and the amount of movement of a particle. This means that the precision with which properties of microscopic objects, such as position and momentum, can be measured is limited and the limit is set by an equation where Planck's constant is the main subject.[citation required ]
The uncertainty principle in one dimension (for example, along the x-axis) is written:
- Δ Δ xΔ Δ px 2=h4π π {displaystyle Delta x,Delta p_{x}gtrsim {frac {hbar}{2}}}={frac {h}{4pi }}}qquad }
Δ Δ x{displaystyle Delta x,}: indetermination in position.
Δ Δ px{displaystyle Delta p_{x},}: indetermination in the amount of movement.
h{displaystyle h}: Planck constant.
Similarly, the uncertainty relationship in any of the spatial projections (about the y or z coordinate axes) can be considered.
Uncertainty is not derived from the measuring instruments but from the very act of measuring; with the most precise devices the uncertainty in the measurement continues to exist. Thus, the greater the precision in the measurement of one of these magnitudes, the greater the uncertainty in the measurement of the other complementary variable. The position and momentum of a particle, with respect to one of the coordinate axes, are complementary magnitudes subject to the restrictions of the Heisenberg uncertainty principle. They are also complementary variables affected by the uncertainty principle for the same object, its energy E and the time, t used in the measurement,
- Δ Δ EΔ Δ t 2=h4π π {displaystyle Delta E,Delta tgtrsim {frac {hbar }{2}{frac {h}{4pi }}qquad }
Application of the uncertainty principle
CERN's LHC (Large Hadron Collider) produces proton collisions at a speed close to that of light. If the protons hit peak speeds vp=2,998× × 108m⋅ ⋅ s− − 1{displaystyle v_{p} =2,998times 10^{8} mcdot s^{1}} and measured with 1% precision, uncertainty can then be calculated in the position of such mass protons m=1,673× × 10− − 27kg{displaystyle m =1,673times 10^{-27}kg} with an approximation of 1% in its speed, and therefore:
Δ Δ vp=(1× × 10− − 2)(2,998× × 108m⋅ ⋅ s− − 1)=2,998× × 106m⋅ ⋅ s− − 1{displaystyle Delta v_{p} =(1times 10^{-2})(2,998times 10^{8}mcdot s^{-1})=2,998times 10^{6}mcdot s^{-1}}}
Given that Δ Δ p=m× × Δ Δ vp{displaystyle Delta p =mtimes Delta v_{p} }of uncertainty in the simultaneous determination of its speed and position is obtained the following relationship Δ Δ x{displaystyle Delta x,},
Δ Δ x≥ ≥ 6,626× × 10− − 34J⋅ ⋅ s(4π π )(1,673× × 10− − 27kg)(2,998× × 106m⋅ ⋅ s− − 1)≥ ≥ 6,62663,029× × 10− − 13m{displaystyle Delta xgeq {frac {6,626times 10^{-34}Jcdot s}{(4pi)(1,673times 10^{-27}kg)(2,998times 10^{6}cdot s^{-1}}}}{geq {frac {6.
Therefore, Δ Δ x≥ ≥ (± ± 1,05× × 10− − 14m){displaystyle Delta x geq (pm 1,05times 10^{}m)}It's the indetermination in the proton position.
Under the same precision conditions, and following the uncertainty principle, it is found that the greater the velocity of the particle, the less its positional uncertainty and vice versa. An extreme example would be the case of a proton at very low speeds, then its position would be very localized in space but, on the other hand, its uncertainty about said position would be great.
Macroscopic application of the uncertainty principle
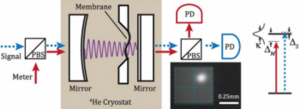
An article published in the journal Science in February 2013 shows that the effects of quantum mechanics are not only clearly measurable in microscopic experiments, but can also be observed in macrophysics. This is the case of a macroscopic oscillator that consists of a membrane located inside an optical cavity and whose position can be measured thanks to the light that is reflected at both ends of the cavity.
An analogy for the optical measurement of the position of an object is the one that is carried out with the autofocus system of a photo camera. By emitting a pulse of infrared light, it reflects off the object and returns to the camera. The time taken by the beam to go and return is used by the camera to estimate the distance between the object and the image plane. The authors have been able to verify how the position of the membrane is affected by the radiation pressure due to the radiation incident on the membrane. The measurement is so precise that it is influenced by the quantum nature of the photons and the systematic error of the measurement is only limited by the quantum noise predicted by the Heisenberg uncertainty principle, equation (1). The aforementioned principle leads to changes in the intensity of the detected light that allow the recoil of the membrane due to radiation pressure to be measured.
New understanding in physics
The work published in the journal Science, in addition to representing progress in the observation of quantum phenomena, constitutes a milestone in the measurement of this type of event, since the experiment reaches the limits of precision imposed by the Heisenberg uncertainty principle in the optical measurements of the position of an object (membrane in an optical cavity). of radiation, RPSN (Radiation Pressure Shot Noise) which is the recoil experienced by the photon when colliding with the object. By Heisenberg's principle, this “shot noise” presents an uncertainty in the amount of movement, Δp, which leads to an error in the position measurement Δx. This relationship has imposed an upper limit on the sensitivity of experiments of this type. The new procedure published in Science allows to measure the position of an object with an error limited only by the RPSN. With these experiments it is possible to verify theoretical procedures used to try to avoid the limit imposed by the uncertainty principle, such as the use of compressed light with minimum uncertainty (quadrature-squeezed light) or techniques to avoid recoil.
Experimental measurements of Planck's constant
Current determination of the constant
Thanks to the precision of current technology, Planck's constant can be determined to at least nine significant figures, and its experimental determination is made from the following experiences:
- The constant of Josephson KJ, obtained thanks to experiments related to the Josephson effect and the quantitativeization of the magnetic flow.
- The constant of von Klitzing. and the Hall resistance of the Quantum Hall effect
- The constant of fine structure.
- Watt's balance, Planck's constant and the redefinition of the kilogram.
- Bohr's magnet in the nuclear magnetic resonance.
- With the current definition of the International Unit System (IS), a measure of the number of Avogadro NA represents an indirect measure of Planck's constant. For this determination of the Avogadro Number use the ratio of the volume to the volume of the unit cell in a Si crystal.
- Measures taken in the LHC laboratories (Great Hadron Colisionator).
Although Planck's constant is associated with microscopic systems, the most precise way to obtain it derives from macroscopic phenomena such as the quantum Hall effect and the Josephson effect.
The constant in the definition of SI units
It was Planck himself who advanced the idea of establishing the units used in physics from the universal constants. The first measurements of the constant were made from the photoelectric effect. For several decades, new experiments were being optimized that made it possible to measure other physical phenomena directly affected by the constant, as well as other constants such as elementary charge and Avogadro's number. As experimental techniques have evolved, the precision of the value of h has also improved; In 1960 the SI (International System of Units) was introduced and with it the definition of the electrical units of V (volt), and the ohm (Ohm) but it was in the decade of the 90s when the ohm was defined for the first time. from the fundamental constant h measuring the Hall resistance in the quantum Hall effect and the volt, from the Josephson effect. Thus, a new SI was born based on very few fundamental constants for its definitions. The theories of the Josephson effect and the quantum Hall effect have played a crucial role in showing the influence of the constant h on the guidelines for electrical measurements, as these have led to new electronic devices. The constant h has not only become essential in the definitions of the units of volts and ohms, but measurements of these effects have made it possible to determine h directly and with even greater precision. As of May 20, 2019, Planck's constant is a value without uncertainty:
- h=6,62607015× × 10− − 34J⋅ ⋅ s{displaystyle h=6,626 070times 10^{-34} {mbox{J}}{cdot {mbox{s}}}}}
Without the refinement of the measurements of the quantum Hall effect and the Josephson effect, in a more basic way although with less precision, the constant h can also be determined at the level of a university teaching laboratory, which has traditionally been obtained from of the photoelectric effect. However, due to the progress achieved in LED technology, experiments to measure the constant h using LED diodes are becoming more frequent.[citation needed]
Estimation of Planck's constant with LED diodes in the university laboratory
Physical foundation
LED diodes are electronic components made of semiconductor materials that, when electric current passes through, emit light. The electronic foundation of the process is the same as that of conventional semiconductor diodes used as rectifiers and which will be explained below, paying attention to the differences with LEDs. In practice LEDs are used as light emitters due to their high performance. The emission is known as cold light due to the low heating that an LED diode has when emitting light. In their operation, diodes are made up of two layers with different electrical properties, one more positive —' zone P'— and the other more negative —'zone N'— in direct contact —zone of the 'PN junction'-. Specifically, the N zone is doped with more electrons than would naturally exist and in the P zone electrons are removed to create 'holes'. When contact is established between the two portions, the excess electrons from the N region pass to the P region and occupy the holes in the contact zone. When filling a hole, a negative ion is created in the P zone and leaves behind a positive ion in the N zone. With this, a space charge accumulates in the contact zone, until reaching a certain equilibrium, creating an electric field at the junction between the two layers that acts as a permanent potential barrier in the absence of an electric generator and does not allow the passage of new electrons from the N to the P region. The area of the junction where the charge has accumulated is called the region depletion or depletion. Externally, the electric field or potential barrier established in a PN junction can be modified by applying an electric generator. If the positive pole is applied to zone N and the negative pole to zone P (what is known as inverse polarization) it will contribute to increase the height of the potential barrier and the current that will flow from the positive pole to the negative pole at across the PN junction will be very weak. On the contrary, if the positive pole of the generator is applied to the P region and the negative to the N region (what is known as direct polarization), the height of the potential barrier will be reduced and the current will be able to flow between the + pole. and the pole - through the PN junction. In an LED diode, if the PN junction is polarized directly, making the P region positive in relation to the N region, the intensity of the field is reduced, thus lowering the potential barrier and allowing the displacement of the charges, the establishment of the current and the emission of photons. The physical phenomenon that takes place in the PN junction when the direct polarization current passes consists of a succession of electron-hole recombinations. The phenomenon of recombination is accompanied by the emission of some type of energy. In ordinary Germanium or Silicon diodes, phonons or vibrations of the crystalline structure of the semiconductor are produced, which simply contribute to its heating. In the case of LED diodes, the structural materials are different from the previous ones, being, for example, various alloys of gallium arsenide. In these semiconductors, the recombinations that take place at the PN junctions remove excess energy by emitting light photons. The color of the emitted light is characteristic of each specific alloy and depends on its frequency. Currently, alloys are manufactured that produce light photons of various colors.
From an external voltage value (which depends on the type of semiconductor material), the LED starts to emit photons, is the ignition voltage V0{displaystyle V_{0}}. Cargo carriers, electrons and hollows can be moved through the union when applied to different electrodes tensions. By elevating the external voltage to the union, the LED starts to drive; from the ignition voltage V0{displaystyle V_{0}}, begins to emit photons and higher tensions, increases the light intensity emitted. This increase in luminous intensity by increasing current intensity can be reduced by Auger recombination . During the re-engineering process, the electron jumps from the driving band to the valence by issuing a photon and accessing, for energy conservation, to a lower level of energy, below the Fermi level of the material. The emission process is called radiative recombination, which corresponds to the phenomenon of spontaneous emission. Thus, in each radiative recombination electron-bone, an energy photon equals the width in energies of the forbidden band is issued, Eg{displaystyle E_{g}} (see figure):
Eg=hf=hcλ λ (2){displaystyle E_{g}=hf={frac {hc}{lambda }qquad (2)}where c is the speed of light and λ is the wavelength of the light it emits. This description of the foundation of the emission of electromagnetic radiation by the LED diode (there are LEDs that also emit in the ultraviolet and in the infrared) can be seen in the figure where a schematic representation of the PN junction of the semiconductor material is made together with the energy diagram, involved in the process of recombination and emission of light, in the lower part of the drawing. The wavelength of the emitted light, and therefore its color, depends on the width of the band gap of energy. In silicon or germanium diodes, electrons and holes recombine, generating lattice vibrations in the form of phonons and emitting thermal radiation. It is a non-radiative transition that ultimately causes the diode to heat up instead of emitting light. The most important substrates available for light emission applications are GaAs and InP. LED diodes can reduce their efficiency if their spectral absorption and emission peaks as a function of their wavelength are very close, as is the case with GaAs:Zn (Zinc-doped) LEDs, since part of the light they emit, They absorb it internally.
The materials used for LEDs have a forward-biased bandgap whose width in energies ranges from infrared light to visible light or even near ultraviolet. The evolution of LEDs began with infrared and red gallium arsenide devices. Advances in materials science have allowed devices with increasingly shorter wavelengths, emitting light in a wide range of colors. LEDs are generally fabricated on an N-type substrate, with an electrode connected to the p-type layer deposited on its surface. P-type substrates, although less common, are also manufactured.
Experimental results
As described in the foundation, a LED requires reaching a certain voltage applied to its terminals V0{displaystyle V_{0}}in direct polarization, for it to emit light. This LED power voltage, V0{displaystyle V_{0}} is proportional, in energies, to the width of the forbidden band Eg{displaystyle E_{g}}:
Eg=eV0+Δ Δ E(3),{displaystyle E_{g}=eV_{0}+Delta Eqquad qquad (3),}
where e is the charge of the electron. Also, remembering eq. (2),
Eg=EFortorn=hf(4),{displaystyle E_{g}=E_{rm {Photon}}=hfqquad (4),}
In fact, this proportionality in energies between the gap Eg{displaystyle E_{g}} and the energy of “engaged” eV0{displaystyle eV_{0}} and between the gap and the energy of the photon, is approximate. While depending on the semiconductor LED material, the emission frequency is determined, because different doping materials are used with the same semiconductor substrate, the energy associated with the leap of the electron from the driving band to the valence is somewhat lower. Due to the approach made, an additive constant is included in the equation (3) Δ Δ E{displaystyle Delta E} which makes it more realistic and allows a better fit for experimental measures.
The "input" voltage has an interpretation of interest from the characteristic LED curve as explained below. In the elbow of the same (see illustration) and in direct polarization, it is precisely where the tension is located V0{displaystyle V_{0}}which is different from one LED to another. For tensions less than the power voltage the current is very weak and the voltage in LED terminals is not enough to produce a statistically significant photon emission. For tensions corresponding to the beginning of the curve elbow and to a determined current intensity, the same for all the LEDs considered, is where the beginning of the light emission is considered.
So equations (3) and (4) become
eV0+Δ Δ E=hf(5){displaystyle eV_{rm {0}+Delta E=hfqquad (5)}
To estimate the Planck constant, equation (5) is used. Measuring the ignition voltage V0{displaystyle V_{0}} of different LEDs depending on their emission frequency f{displaystyle f} and performing the adjustment by a straight line according to this equation, is obtained h{displaystyle h} like the slope of the same, regardless of the value of Δ Δ E{displaystyle Delta E}.
It is convenient to choose suitable characteristics, commercially accessible and common to the different LEDs that are to be used for the measurements, such as a diameter of 5 mm, a luminosity of about 120 lumens or the power consumed in the order of 3w.
Obtaining the wavelength of an LED
Although the technical sheets of the LED diode manufacturers show the values of the emitted wavelengths, they can also be measured in a university teaching laboratory. For this, a spectrum analyzer is used. In this case, measurements made with the AQ-6315A / -6315B analyzer will be displayed. The light signal reaches the analyzer through an optical fiber. The origin of the fiber is located in front of the LED diode and is located by means of a '3D positioner'. The fiber is centered on the diode with the help of reading the current supplied by a Si photodetector.
The analyzer provides the optical power captured by the fiber as a function of λ and its result is given in dBm (decibels referred to 1 mW). The analyzer sensitivity reaches -60 dBm. For each diode, the region of emitted wavelengths must be explored and analyzed in detail.
The spectrum analyzer allows to determine the different luminosity of the diodes depending on the manufacturing material.
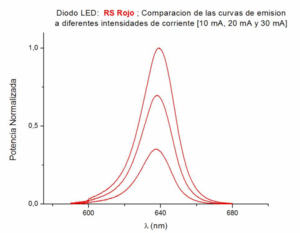
As the luminous intensity of the LED increases, a dependence of the luminosity curves with temperature appears, displacing the maximum of the curve to longer wavelengths. For this reason, it is convenient to carry out the measurements by applying weak currents to the LED, as in the figure, where the curves corresponding to the weakest currents of 10 mA are shown. The results measured with the spectrum analyzer correspond well with the manufacturers' data.
It can be seen in the figure, in the case of a red Led RS, the effect of temperature in the small displacement of the maximum of the curve towards longer wavelengths when the intensity of the current through the Led is increased,.
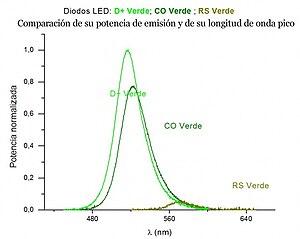
In a brief analysis of the luminosity for Led diodes with the same characteristics of 5 mm in diameter and around 120 lumens , the behavior can be observed as a function of the direct current for different colors. For this, the values of the wavelength are represented on the horizontal axis and on the vertical axis, the normalized emitted light power. The three curves that accompany the text correspond to direct current values of 10, 20 and 30 mA. Each LED diode has been associated with the wavelength corresponding to the maximum of the luminosity curve. Among all the LED diodes measured, the seven that showed a greater luminosity and reasonably covered the optical spectrum have been selected. And in the following figure, it can be seen by comparing their luminosity curves, that the D+ Green and CO Green diodes present a good behavior in terms of luminosity and emission characteristics, not being the case for the RS Green with worse emission characteristics.
Layout of the characteristic curves of the LED diodes. Experimental determination of ignition voltages
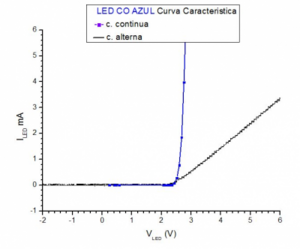
Since it is about obtaining Planck's Constant, it is very important to have very well defined and measured the ignition voltage (Vo) and pay special attention to the differences in the measurements made with a power supply with direct or alternating voltage or even using a ramp voltage. To see these differences, two procedures for measuring the ignition voltage in the laboratory are shown, for LED diodes using different colors. The first, implementing the measurement circuit powered by a direct voltage source and in the second, the circuit is powered by an e.m.f. alternate. In both cases, the characteristic curves of the LED diodes, I = I (V), are obtained, taking special care to better identify the voltage at the bend of the curve. It should be noted that this is precisely the non-linear part of the diode's characteristic curve. In an ideal diode, this zone is simplified by being limited to a vertex, where the slope between two linear zones changes. On the other hand, for the measurement of the Constant, the zone of the elbow of the curve is very important.
In the animation you can see the simplified electrical diagram that is used to determine the characteristic curve of LED diodes in direct current, point to point, for the values (current I – voltage V). To carry it out, the voltage V of the generator is gradually increased, measuring the voltage at the terminals of the diode V and the current I that passes through it at each increase. To obtain the aforementioned curve, when the circuit is powered by a direct voltage generator, the I= I (V) values are represented for each LED, obtained point by point, measuring in particular the I-V values in the elbow area of the the curve, as can be seen in the figure of the characteristic curve for the green CO and blue CO diodes.
By inverting the polarity of the generator, the branch of the characteristic curve corresponding to the area of negative voltages is obtained. The current intensity in this area is, as can be seen in the curve for the red LED RS, very weak. With the second procedure, the measurement circuit is basically the same as the animation circuit, but substituting the DC source for an e.m.f. of alternating that allows to verify the rectifying function of the diode in inverse polarization. As the power supply is periodic, an oscilloscope or a data acquisition card can be used to store the characteristic curve in great detail since, for example, in a 1 ms interval, 10 periods of a 10 kHz signal are stored. frequency. By this procedure, the series of measurements (current I, voltage V) can be recorded with, for example, the Picoscope 6 data acquisition card. As a result of these measurements, a characteristic curve I= is displayed for the Red RS LED. I (V), part a) and to the right, part b) the temporal evolution of both the current and the supply voltage, observing the rectification of the current produced by the LED diode.
To complete the measurement procedures and analyze the influence of other wave generators, it is convenient to measure the characteristic curve of the LED diodes, replacing the DC generator with a triangular wave generator and a sine wave generator. In these two cases, the complete trace of the characteristic curve is obtained, a data acquisition card can be used, or a digital oscilloscope with which the measurements are also collected with great precision. Both the triangular wave and the sinusoidal wave, under the same measurement conditions, give a very similar behavior in the elbow area.
With the intention of obtaining greater precision in determining the ignition voltage (Vo) it is interesting to compare the measurements of the first procedure in DC, with those of the second, in DC in the elbow area. This comparison can be seen in the figure for the blue CO LED. In this area where the current that passes through the LED is low, in the range of 0.02 to 0.1 mA, the coincidence of the two types of measurements is very good and allows us to specify the "take off"; of the curve at the moment of 'on' of the LEDs.
The following table shows the values of λ measured in the teaching laboratory and the values of the ignition voltage deduced by comparing the measurements obtained in alternating current and with the corresponding ones in direct current, explained in this section.
'Experimental values obtained for the wavelengths and for the switching voltages for seven LEDs of different wavelengths'.
| Color | Long. onda λ (nm) | Voltage Vor (V) |
|---|---|---|
| RS Violeta | 425 | 2.95 |
| CO Blue | 470 | 2.55 |
| D+LED Green | 525 | 2.35 |
| CO Green | 529 | 2.37 |
| RS Ambar | 610 | 1.67 |
| RS Red | 643 | 1.75 |
| RS Infrared | 887 | 1.19 |
Obtaining Planck's constant from frequency and threshold voltage
The following table summarizes the experimental values necessary to determine Planck's constant by a university laboratory procedure. The first column shows the LED diodes used, the second column shows the emission characteristic frequency of each of them, and the third shows the width of the forbidden band determined experimentally, expressed in energy units. The fourth column shows an estimate of Planck's constant calculated from the measured values for each LED.
| Color | Frequency f=c/λ (Hz) | E=qVor=hf (J) | ≤2 |
|---|---|---|---|
| RS Violeta | 7,44×1014 | 4,47×10-19 | (6.79 ± 0.06) × 10- 34 J. s R2 = 0.9953 |
| CO Blue | 6,41×1014 | 3,99×10-19 | |
| D+LED Green | 5,81×1014 | 3,81×10-19 | |
| CO Green | 5,75×1014 | 3,77×10-19 | |
| RS Ambar | 4,96×1014 | 2,74×10-19 | |
| RS Red | 4,70×1014 | 2,72×10-19 | |
| RS Infrared | 3,37×1014 | 1,89×10-19 |
The definitive value of the Planck constant is determined by the seven experimental points (f,E){displaystyle (f,E)}And adjusting them to a straight line. The slope of the adjusted line is a good estimate of the Planck constant.
To complete the determination, the seven points result of the measures, of coordinates, are represented (f,eV0){displaystyle (f,eV_{0})}. In the same the chart appears the line corresponding to the set, equation (5), according to explanation given at the beginning of the section. The adjustment result provides a value
h=(6,79± ± 0,06)× × 10− − 34J.s{displaystyle h=(6,79pm 0.06)times 10^{-34}J.s}
This result, although it is an estimate of the constant since it appreciates only the first significant figure, it is adequate considering the simplicity of the method used to obtain it. This measurement procedure is also used as an introduction to quantum mechanics for science and engineering students. Of the very diverse existing works in university teaching laboratories and by way of comparison, three references that use this method to obtain Planck's Constant are included: One from the University of Pennsylvania, another from the Cornell Center for Material Research, and finally a reference from the University of Buenos Aires. In this last reference, the value obtained for Planck's constant is compared with that obtained by two other methods in which they consider the Shockley model for the diode and which, however, do not obtain a better estimate.
Contenido relacionado
Curie (unit)
Centisecond
Linear accelerator