Pentagon

ImprimirCitar

A regular pentagon and its main angles

In geometry, it is called a pentagon (from the Greek πεντάγωνον, from πέντε pénte "five" and γωνία gōnía & #34;angle") to a polygon with five sides and five vertices.

Definition

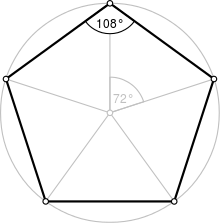
A regular pentagon is one that has all its sides equal and its internal angles congruent.

Propositions

Each inner angle measures 108 degrees or 3π π /5{displaystyle 3pi /5} ${displaystyle 3pi /5}$ radian.
- It's convex.
Each external angle of the regular pentagon is 72°.
He's got exactly five diagonals.
A regular pentagon can be registered as circumscribed in circumcentric circles.
The two diagonals that depart from a common vertex determine in the pentagon three triangles in succession, one in the middle: isosceles, whose equal sides are the diagonals; two triangles equal to the sides of the former, are also isosceles for having as equal sides, two of the sides of the regular pentagon.
The interesting thing is that the two diagonals trisecan at the angle of which the vertex part, since each angle is 36°, the sum of which gives the angle at the vertex of 108°.

Properties

Apothem

The nickname, ${displaystyle a_{p}}$ Of a regular pentagon side $L$ That's it.

{displaystyle a_{p}={frac {L}{2}}cdot {sqrt {1+{frac {2}{sqrt {5}}}}}}

Area

The area of a regular pentagon side $L$ That's it.

{displaystyle A={frac {5L^{2}}{4}}cot {frac {pi }{5}}={frac {L^{2}}{4}}{sqrt {25+10{sqrt {5}}}}simeq 1,72048L^{2}}

Or, depending on the radius of the circumscribed circle, $r$ ,

{displaystyle A={frac {5}{8}}cdot r^{2}cdot {sqrt {10+2{sqrt {5}}}}}

or,

{displaystyle A={frac {5}{2}}cdot r^{2}cdot sin {72^{circ }}}

And depending on the apothema, ${displaystyle a_{p}}$

{displaystyle A=5a_{p}^{2}cdot {sqrt {5-2{sqrt {5}}}}}

Perimeter

The perimeter of a regular pentagon side $L$ That's it.

{displaystyle P=5cdot L}

Or, depending on the apotheme ( ${displaystyle a_{p}}$ ),

{displaystyle P=10cdot a_{p}cdot {sqrt {5-2{sqrt {5}}}}}

Formula to calculate interior angles

The sum of the interior angles of a pentagon is 540°.

The general formula to calculate the sum of the interior angles of any regular polygon (in the case of the pentagon n = 5) is:

{displaystyle sum {alpha =}(n-2)cdot 180^{circ }=3cdot 180^{circ }=540^{circ }}

The angle between two sides of a regular pentagon can be calculated using the following formula (in the pentagon, n = 5):

{displaystyle alpha ={frac {(n-2)}{n}}cdot 180^{circ }={frac {3}{5}}cdot 180^{circ }=108^{circ }}

Movements

The regular pentagon is a symmetrical figure with respect to the axis that contains an apothesis and its prolongation that passes through the vertice opposite the base of the apothesis.
There are five axes of symmetry
Five rotation cases: 72°, 144°, 216°, 288° and 360°

Construction of a regular pentagon

Graphical sequence using rule and compass

A regular pentagon is constructible using a compass and straightedge, either by inscribing one in a given circle or by constructing one on a given side. Euclid described this process in his Elements, around 300 B.C. C.

A regular pentagon, inscribed in a circle (see the figure), can be constructed with a ruler and compass as follows:

We cross two straight lines perpendicular to the center O of the circumference (PD and OQ in the figure). We determine the M midpoint of the OQ segment and trace the PM straight. With center in M, we trace the MO radio circle. Let us note with R and S the intersections of this circumference with the PM straight. The center circles in P and PR and PS radios determine the vertices of the regular pentagon.

Joining the vertices of the pentagon, you get a pentagram (5-pointed star) inscribed on it. In the center there will be another regular pentagon, with which the process of inscribing pentagrams in the successive pentagons that are generated, mathematically, has no end.

By inscribing a pentagram in a regular pentagon, you can observe the golden ratio between the lengths of the resulting segments.

Geometric relations of the regular pentagon

Relationship with the golden ratio

Pentagram and Pentagon

Let's see that the ratio between a segment that joins two of its non-consecutive vertices and one of the sides of the pentagon is the golden ratio or golden number, for example that

{displaystyle CE=left({frac {1+{sqrt {5}}}{2}}right)CD}

By symmetry, segments CE and CA are equal. We observe that the triangles ANF and CMF are similar. From the similarity of their sides we have that

{displaystyle {frac {MC}{AN}}={frac {FC}{AF}}}

Note that MC is half CE and AN is half AB. On the other hand, since the triangle FCD is isosceles, we have that FC = CD. Thus we can write AF = AC - FC = CE - CD. Therefore

{displaystyle {frac {CE}{CD}}={frac {CD}{CE-CD}}={frac {1}{CE/CD-1}}}

Replace CE/CD by $varphi$ We've got

{displaystyle varphi ={frac {1}{varphi -1}}qquad ,(1)}

in other words ${displaystyle varphi -1={frac {1}{varphi }}}$ . This equation describes the golden reason. $varphi$ It's the only positive number that when we subtract the unit, we get its reverse.

Some considerations about triangles

Let us consider a (regular) pentagon and the circumcircle of said pentagon. Let's draw the perpendicular through the center of the circle to the side DA of the pentagon and let M be the intersection of this perpendicular with the circle, the angle AOB measures 360°/5=72° and the angle AOM is its half, that is to say 36°. The angle MOB, the sum of these two is worth 108° and since the triangle AOB is isosceles we have that

The reason between the MB segment and the OM radius of the circumference is the golden reason
${displaystyle angle BMO=(180^{circ }-108^{circ })/2=72^{circ }/2=36^{circ }}$

Thus, be P the intersection of the OA and MB straights. The PMO triangle is isosceles, and the reason between the OM radio and the PM segment is the golden reason. Finally, the triangle OBP is also isosceles, with what PB = OB (=OM). We have: ${displaystyle {frac {PM}{OM}}={frac {1}{varphi }}={frac {MB-PB}{OM}}=varphi -1}$

The above can be interpreted as a geometric proof of equation (1).

Contenido relacionado

Más resultados...