Pendulum

ImprimirCitar

Simple shape in harmonic motion with small oscillations.

Pendulum in Metropolitan Cathedral, Mexico City.

The pendulum (from the Latin pendŭlus, slope) is a physical system that can oscillate under gravitational action or another physical characteristic (elasticity, for example) and that It is configured by a mass suspended from a fixed point or horizontal axis by means of a thread, a rod, or another device that can keep the system fixed.

There are many different types of pendulums that, according to their configuration and uses, receive the appropriate names: simple pendulum, compound pendulum, cycloidal pendulum, double pendulum, Foucault pendulum, ballistic pendulum, torsion pendulum, spherical pendulum, among others. others.

Its uses are very varied: measurement of time (pendulum clock, metronome,...), measurement of the intensity of gravity, etc.

History

Replica of the seismometer of Zhang Heng. The pendulum is contained inside.

One of the earliest known uses of a pendulum was a seismometer device from the 1st century Han dynasty Chinese scientist Zhang Heng. Its function was to swing and activate one of a series of levers after being disturbed by the tremor of a distant earthquake. Released by a lever, a small ball fell from the urn-shaped device into one of the eight metal toad mouths below, at the eight points of the compass, signifying the direction in which the earthquake was located.

Many sources claim that the 10th-century Egyptian astronomer Ibn Yunus used a pendulum to measure time, but this is an error originating in 1684 by the British historian Edward Bernard.

During the Renaissance, large hand-pumped pendulums were used as power sources for reciprocating hand-operated machines such as saws, bellows, and pumps. Leonardo da Vinci made many drawings of pendulum motion, although he was unaware of it. its value for the measurement of time.

1602: Galileo's Investigations

Italian scientist Galileo Galilei was the first to study the properties of pendulums, beginning around 1602. The first surviving report of his investigations is contained in a letter to Guido Ubaldo dal Monte, from Padua, dated November 29, 1602. His biographer and student, Vincenzo Viviani, indicates that his interest had aroused around 1582 in the oscillatory motion of a chandelier in the cathedral of Pisa. Galileo discovered the important property that makes the pendulum a useful tool for measuring time, called isochronism; the period of the pendulum is approximately independent of the amplitude or displacement of the swing.He also discovered that the period is independent of the mass of the bob and proportional to the square root of the length of the pendulum. He first used free-swinging pendulums in simple timing applications. His doctor friend, Santorio Santorii, invented a device that measured a patient's pulse by the length of a pendulum; the pulsilogium .In 1641 Galileo dictated to his daughter Vincenzo the design of a pendulum clock, Vincenzo began construction of it, but had not finished it when he died in 1649.

1656: The Pendulum Clock

The first pendulum watch

In 1656 the Dutch scientist Christiaan Huygens built the first pendulum clock. This was a vast improvement over existing mechanical clocks; their greatest accuracy went from about 15 minutes of deviation per day to about 15 seconds per day. Pendulums spread across Europe as existing clocks were retrofitted with them.

The English scientist Robert Hooke studied the conical pendulum around 1666, consisting of a pendulum that swings freely in two dimensions, with the coil rotating in a circle or ellipse. He used the movements of this apparatus as a model to analyze the movements orbitals of the planets. Hooke suggested to Isaac Newton in 1679 that the components of orbital motion consisted of inertial motion along a tangent direction plus attractive motion in the radial direction. This played a role in Newton's formulation of the law of universal gravitation. Robert Hooke was also responsible for suggesting as early as 1666 that the pendulum could be used to measure the force of gravity.

During his expedition to Cayenne, French Guiana in 1671, Jean Richer discovered that a pendulum clock was 2¹⁄₂ minutes per day slower in Cayenne than in Paris. From this he deduced that the force of gravity was less in Cayenne.

Simple or mathematical pendulum

Main article: Simple

Components of the weight of the pendular mass.

Also called ideal pendulum, it is made up of an inextensible thread of negligible mass, supported by its upper end from a fixed point, with a point mass attached to its lower end that oscillates freely in a plane fixed upright.

When separating the pendulum mass from its equilibrium point, it oscillates to both sides of said position, moving on a circular path with periodic movement.

Equation of Motion

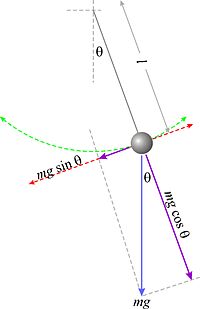
To write the equation of movement we will observe the attached figure, corresponding to a generic position of the pendulum. The blue arrow represents the weight of the pendulum mass. The purple arrows represent the weight components in the tangential and normal directions to the trajectory.

Applying Newton's Second Law in the direction of motion, we have

$F_{{text{t}}}=-mgsin theta =ma_{{text{t}}},$

where the negative sign takes into account $F_{{text{t}}}$ has opposite direction to that of the positive angular displacement (doing the right, in the figure). Considering the relationship between tangential acceleration and angular acceleration

$a_{{text{t}}}=ell {ddot theta } ,$

we finally obtain the differential equation of the plane motion of the simple pendulum

${displaystyle ell {ddot {theta }} +gsin theta =0,}$

Swing Period

Amplifying the period of a pendulum, for any angular width. For small angles the factor is approximately 1 but tends to infinite for angles close to π (180o).

The Italian astronomer and physicist Galileo Galilei observed that the oscillation period is independent of the amplitude, at least for small oscillations. Instead, that depends on the length of the thread. The period of the oscillation of a simple pendulum restricted to oscillations of small amplitude can be approximated by:

$Tapprox 2pi {sqrt {ell over g}}$

For larger oscillations the exact relationship for the period is not constant with the amplitude and involves elliptic integrals of the first kind:

{displaystyle T=4{sqrt {ell over g}}Kleft(sin {frac {varphi _{0}}{2}}right)=4{sqrt {ell over g}}int _{0}^{frac {pi }{2}}{frac {dtheta }{sqrt {1-sin ^{2}{frac {varphi _{0}}{2}}sin ^{2}theta }}}}

Where φ₀ is the maximum angular amplitude. The previous equation can be developed in a Taylor series obtaining a more useful expression:

T=2pi {sqrt {ell over g}}left[1+left({frac {1}{2}}right)^{2}sin ^{2}{frac {varphi _{0}}{2}}+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}{frac {varphi _{0}}{2}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right)^{2}sin ^{6}{frac {varphi _{0}}{2}}+dots right]

Solution of the equation of motion

For small oscillations the amplitude is almost senoidal, for larger amplitudes the oscillation is no longer senoidal. The figure shows a wide movement

phi _{0}=0,999pi

(black), together with a small-scale movement

phi _{0}=0,25pi

(gris).

For small amplitudes, the oscillation can be approximated as a linear combination of trigonometric functions. For large amplitudes it can be proved that the angle can be expressed as a linear combination of Jacobi elliptic functions. To see this, it is enough to take into account that energy constitutes an integral of movement and use the quadrature method to integrate the equation of movement:

${displaystyle t={sqrt {frac {m}{2}}}int _{0}^{phi (t)}{frac {ldtheta }{sqrt {E-U(theta)}}}=}$ $={sqrt {{frac {l}{2g}}}}int _{0}^{{phi (t)}}{frac {dtheta }{{sqrt {cos theta -cos phi _{0}}}}}={sqrt {{frac {l}{4g}}}}int _{0}^{{phi (t)}}{frac {dtheta }{{sqrt {sin ^{2}{frac {phi _{0}}{2}}-sin ^{2}{frac {theta }{2}}}}}}$

Where, in the last expression, the double angle formula has been used and where in addition:

E=-mglcos phi _{0};

, it is the energy, which is related to the maximum amplitude

phi _{0};

U(phi)=-mglcos phi ;

It's the potential energy.

Making variable $sin xi ={frac {sin {frac {theta }{2}}}{sin {frac {phi _{0}}{2}}}};$ the solution of the equations of the movement can be expressed as:

${displaystyle t={sqrt {frac {l}{g}}}int _{0}^{Phi }{frac {dxi }{sqrt {1-sin ^{2}{frac {phi _{0}}{2}}sin ^{2}xi }}}Rightarrow theta (t)=2arcsin left({mbox{sn}} {sqrt {frac {g}{l}}}tcdot sin {frac {phi _{0}}{2}}right)}$

Where:

{mbox{sn}}(t);

, it's Jacobi's elliptical function as a breast.

sin Phi ={frac {sin {frac {phi (t)}{2}}}{sin {frac {phi _{0}}{2}}}}

The lagrangian system is ${mathcal {L}}=T-V={frac {1}{2}}ml^{2}{dot {theta }}^{2}+mglcos {theta }$ Where $theta$ is the angle that forms the pendulum string along its oscillations (it is the variable), and $l$ is the length of the rope (it is the ligature). If the equations of Lagrange are applied, the final equation of the movement is reached: $l^{2}{ddot {theta }}+glsin {theta }=0$ . That is, the mass does not influence the movement of a pendulum.

Spherical pendulum

Main article: Spherical Péndule

Péndule de Foucault in the southern hemisphere.

A spherical pendulum is a system with two degrees of freedom. The movement is confined to a portion of the spherical surface (of radius l) between two parallels. There are two integrals of motion, the energy E and the component of angular momentum parallel to the vertical axis M_z. The Lagrangian function is given by:

$L={frac {1}{2}}ml^{2}({dot {theta }}^{2}+{dot {phi }}^{2}sin ^{2}theta)+mglcos theta$

Where $phi$ is the polar angle and $theta$ is the angle that forms the thread or pendulum bar with the vertical. The equations of movement, obtained by introducing the previous lagrangian in the equations of Euler-Lagrange are:

${displaystyle {begin{matrix}{cfrac {d}{dt}}{cfrac {partial L}{partial {dot {theta }}}}-{cfrac {partial L}{partial theta }}=0&Rightarrow &l{ddot {theta }}-l{dot {phi }}^{2}sin theta cos theta +gsin theta =0\\{cfrac {d}{dt}}{cfrac {partial L}{partial {dot {phi }}}}-{cfrac {partial L}{partial phi }}=0&Rightarrow &{cfrac {d}{dt}}(ml^{2}{dot {phi }}sin ^{2}theta)=0end{matrix}}}$

The second equation expresses the constancy of the Z component of the angular momentum and therefore leads to the relationship between the polar spin velocity and the angular momentum and therefore to rewrite the Lagrangian as:

${displaystyle {dot {phi }}={frac {M_{z}}{ml^{2}sin ^{2}theta }}Rightarrow qquad L=K({dot {theta }})+U_{ef}(theta)={frac {1}{2}}ml^{2}{dot {theta }}^{2}+{frac {M_{z}^{2}}{2ml^{2}sin ^{2}theta }}-mglcos theta }$

And the problem is reduced to a one-dimensional problem.

Period

The movement of a spherical pendulum is generally not periodic, since it is the combination of two periodic movements of generally incommensurable periods. However, the movement is quasi-periodic, which means that, given a previous position and speed of the movement, there is a time T such that the movement will pass at a distance as small as desired from that position with a speed as similar as you want, but without repeating exactly. Given that the region of movement is also compact, the set of points the trajectory of a spherical pendulum constitutes a dense set on a spherical area between two spherical caps.

Solution of the equation of motion

The equations of motion can be expressed in terms of elliptic integrals of the first kind and third kind:

${displaystyle t={sqrt {frac {ml^{2}}{2}}}int {frac {dtheta }{sqrt {E-U_{ef}(theta)}}}qquad phi ={frac {M_{z}}{l{sqrt {2m}}}}int {frac {dtheta }{sin ^{2}theta {sqrt {E-U_{ef}(theta)}}}}}$

Contenido relacionado

Más resultados...

Pendulum

History

1602: Galileo's Investigations

1656: The Pendulum Clock

Simple or mathematical pendulum

Equation of Motion

Swing Period

Solution of the equation of motion

Spherical pendulum

Period

Solution of the equation of motion

Contenido relacionado

Big Crunch Theory

Niels Bohr

Amp