Partial pressure
In a mixture of gases, each constituent gas has a partial pressure which is the theoretical pressure of that constituent gas if it occupied by itself the entire volume of the original mixture, at the same temperature. The total pressure of an ideal gas mixture is the sum of the partial pressures of the gases in the mixture (Dalton's Law).
The partial pressure of a gas is a measure of the thermodynamic activity of the gas molecules. Gases dissolve, diffuse, and react according to their partial pressures and not according to their concentrations in mixtures of gases or liquids. This general property of gases is also true of the chemical reactions of gases in biology. For example, the amount of oxygen necessary for human respiration, and the amount that is toxic, is established only by the partial pressure of oxygen. This is true over a wide range of different oxygen concentrations present in various respiratory gases inhaled or dissolved in the blood. Partial pressures of oxygen and carbon dioxide are important parameters in arterial blood gas tests, but they can also be measured in, for example, cerebrospinal fluid.
Symbol
The pressure symbol is generally P{displaystyle {P} or p{displaystyle {p}, which can use a subscript to identify pressure, and gas species are also mentioned by subscript. When combined these subscripts are applied recursively.
Examples:
- P1{displaystyle {P_{1}}} or p1{displaystyle {p_{1}}}= pressure in time 1
- PH2{displaystyle {P_{H_{2}}}}}or pH2{displaystyle {p_{H_{2}}}}}= partial hydrogen pressure
- PvO2{displaystyle {P_{v_{O_{2}}}}}}or pvO2{displaystyle {p_{v_{O_{2}}}}}}= partial oxygen venous pressure
Dalton's law of partial pressures
Dalton's law expresses the fact that the total pressure of a mixture of gases is equal to the sum of the partial pressures of the individual gases in the mixture. This equality arises from the fact that in an ideal gas the Molecules are so far apart that they do not interact with each other. Most of the real gases in the real world come very close to this ideal. For example, given an ideal gas mixture of nitrogen (N2), hydrogen (H2), and ammonia (NH3):
- p=pN2+pH2+pNH3{displaystyle p=p_{{ce {n2}}}}+p_{{{ce {H2}}}}}}}
| where: | |
| p{displaystyle p,} | = total pressure of gas mixture |
|---|---|
| pN2{displaystyle p_{ce {N2}}}}} | = partial nitrogen pressure (N)2) |
| pH2{displaystyle p_{ce {H2}}}}} | = partial hydrogen pressure (H2) |
| pNH3{displaystyle p_{ce {NH3}}}}} | Partial pressure of ammonia (NH)3) |
Ideal Gas Mixtures
Ideally, the ratio of partial pressures is equal to the ratio of the number of molecules. That is, the mole fraction of an individual gas component in an ideal gas mixture can be expressed in terms of the partial pressure of the component or the moles of the component:
- xi=pip=nin{displaystyle x_{mathrm {i} }={frac {p_{mathrm {i}}} }{p}}}{frac {n_{mathrm {i}}}}}}}{n}{mathrm {i}}
and the partial pressure of an individual gas component in an ideal gas can be obtained using this expression:
| Symbol | Name |
|---|---|
| xi{displaystyle x_{i}} | Moulding fraction of any individual gas component in a gas mixture |
| pi{displaystyle p_{i}} | Partial pressure of any individual gas component in a gas mixture |
| ni{displaystyle n_{i}} | Moles of any individual gas component in a gas mixture |
| n{displaystyle n} | Total moles of gas mixture |
| p{displaystyle p} | Total pressure of gas mixture |
The mole fraction of a gas component in a gas mixture is equal to the volume fraction of that component in a gas mixture.
The relationship of partial pressures is based on the following isothermal relationship:
| Symbol | Name |
|---|---|
| Vx{displaystyle V_{x}} | Partial volume of any individual gas component (x{displaystyle x}) |
| Vtort{displaystyle V_{tot} | Total volume of gas mixture |
| px{displaystyle p_{x}} | Partial gas pressure (x{displaystyle x}) |
| ptort{displaystyle p_{tot} | Total pressure of gas mixture |
| nx{displaystyle n_{x}} | Quantity of gas substance (x{displaystyle x}) |
| ntort{displaystyle n_{tot} | Total amount of substance in gas mixture |
Partial volume (Amagat's law of additive volume)
The partial volume of a particular gas in a mixture is the volume of a component of the gas mixture. It is useful in gas mixtures, eg air, to concentrate on a particular gas component, eg oxygen.
Can be approximated from both partial pressure and mole fraction:
Vx=Vtort× × pxptort=Vtort× × nxntort{displaystyle V_{x}=V_{tot}times {frac {p_{x}}{p_{tot}}}}{V_{tot}{times {frac {n_{x}}{n_{tot}}}}}}}}}}}}
- Vx is the partial volume of an individual gas component X in the mixture
- Vtot is the total volume of the gas mixture.
- px is the partial pressure of the X gas
- ptot is the total pressure of the gas mixture
- nx is the amount of X gas substance
- ntot is the total amount of substance in the gas mixture
Vapor pressure
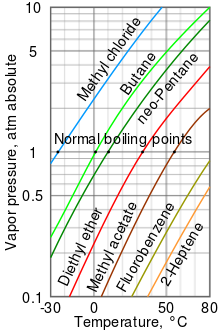
Vapor pressure is the pressure of a vapor in equilibrium with its non-vapor phases (ie, liquid or solid). Most often, the term is used to describe a liquid's tendency to evaporate. It is a measure of the tendency of molecules and atoms to escape from a liquid or a solid. The atmospheric pressure boiling point of a liquid corresponds to the temperature at which its vapor pressure equals the surrounding atmospheric pressure, and is often referred to as the normal boiling point.
The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point of the liquid.
The vapor pressure graph shown has graphs of vapor pressures as a function of temperatures for a variety of liquids. As can be seen from the table, the liquids with the highest vapor pressures have the points lower normal boiling points.
For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the table. It also has the lowest normal boiling point (-24.2 °C), which is where the vapor pressure curve of methyl chloride (the blue line) crosses the horizontal pressure line of one atmosphere (atm) pressure. absolute steam. Note that at higher altitudes, the atmospheric pressure is lower than at sea level, so the boiling points of liquids are lowered. At the top of Mount Everest, the atmospheric pressure is about 0.333 atm, so using the graph, the boiling point of diethyl ether would be about 7.5 °C versus 34.6 °C at sea level (1 atm).
Equilibrium constants of reactions involving gas mixtures
It is possible to calculate the equilibrium constant for a chemical reaction involving a mixture of gases given the partial pressure of each gas and the general reaction formula. For a reversible reaction involving gas reactants and gas products, such as:
- aA+bB▪ ▪ cC+dD{displaystyle a,A+b,Bleftrightarrow c,C+d,D}
The equilibrium constant of the reaction would be:
| Symbol | Name |
|---|---|
| Kp{displaystyle K_{p}} | Constant reaction balance |
| a{displaystyle a} | Reactive coefficient A{displaystyle A} |
| b{displaystyle b} | Reactive coefficient B{displaystyle B} |
| c{displaystyle c} | Product coefficient C{displaystyle C} |
| d{displaystyle d} | Product coefficient D{displaystyle D} |
| pAa{displaystyle p_{A}^{a}} | Partial pressure a{displaystyle a} |
| pBb{displaystyle p_{B}{b}{b}} | Partial pressure b{displaystyle b} |
| pCc{displaystyle p_{C}{c}{c}} | Partial pressure c{displaystyle c} |
| pDd{displaystyle p_{D}{d}{d}} | Partial pressure d{displaystyle d} |
For reversible reactions, changes in total pressure, temperature, or reactant concentrations will shift the equilibrium to favor either the right or left side of the reaction according to Le Chatelier's Principle. However, the kinetics of the reaction can oppose or enhance the equilibrium change. In some cases, reaction kinetics may be the primary factor to consider.
Henry's law and the solubility of gases
Gases will dissolve in liquids to an extent determined by the balance between the undissolved gas and the gas that has dissolved in the liquid (called the solvent). The equilibrium constant for that equilibrium is:
- (1) k=pxCx{displaystyle k={frac {p_{x}}{C_{x}}}}}
where: k{displaystyle k} = the balance constant for the hovering process. px{displaystyle p_{x}} = partial gas pressure x{displaystyle x} in balance with a solution containing some gas Cx{displaystyle C_{x}} = gas concentration x{displaystyle x} in liquid solution
The shape of the balance constant shows that the concentration of a single gas in a solution is directly proportional to the partial pressure of that gas on the solution. This statement is known as Henry's law and constant balance. k{displaystyle k} is often referred to as Henry's law constant.
Henry's law is sometimes written as:
- (2) k♫=Cxpx{displaystyle k'={frac {C_{x}}{p_{x}}}}
where k♫{displaystyle k'}It is also known as Henry's law constant. As compared to the previous (1) and (2) equations, k♫{displaystyle k'}is the reciprocal k{displaystyle k}. Since both can be called as the constant of Henry's law, readers of technical literature must be very careful to notice which version of Henry's law equation is being used. Henry's law is an approximation that only applies to diluted solutions, ideals and solutions where the liquid solvent does not react chemically with the gas dissolved.
Diving
In scuba diving, the physiological effects of individual components of respiratory gases are a function of partial pressure.
Using diving terms, the partial pressure is calculated as:
- partial pressure = total absolute pressure × volume fraction of gas component{displaystyle {text{partial pressure = total absolute pressure × gas component volume fraction}}}}}
For the component gas "i":
- ppi=P↓ ↓ Fi{displaystyle pp_{i}=P*F_{i}}
For example, at 50 meters (164 feet) underwater, the total absolute pressure is 6 bar (600 kPa) (that is, 1 bar atmospheric pressure + 5 bar water pressure) and the partial pressures of The main components of air, oxygen 21% by volume and nitrogen approximately 79% by volume are:
- ppN2 = 6 bar 0.79 = 4.7 bar absolute
- ppO2 = 6 bar × 0.21 = 1.3 bar absolute
| where: | |
| ppi | = partial pressure of the gas component i = Pi{displaystyle P_{mathrm {i}}} |
|---|---|
| PAG | Total pressure = P{displaystyle P} |
| Fi | = c volume fractiongas omponent i = molar fraction, xi{displaystyle x_{mathrm {i}}}} |
| ppN2 | Partial pressure nitrogen = PN2{displaystyle P_{mathrm {N}_{2}}}}} |
| ppO2 | = partial oxygen pressure = PO2{displaystyle P_{mathrm {O} |
The minimum safe lower limit for partial pressures of oxygen in a gas mixture is 0.16 bar (16 kPa) absolute. Hypoxia and sudden unconsciousness become a problem with an oxygen partial pressure of less than 0.16 bar absolute. Oxygen toxicity, which involves seizures, becomes a problem when the partial pressure of oxygen is too high. The NOAA Diving Manual recommends a maximum single exposure of 45 minutes at 1.6 bar absolute, 120 minutes at 1.5 bar absolute, 150 minutes at 1.4 bar absolute, 180 minutes at 1.3 bar absolute and 210 minutes at 1.2 bar absolute. Oxygen toxicity becomes a risk when these pressures and partial oxygen exposures are exceeded. The partial pressure of oxygen determines the maximum operating depth of a gas mixture. Narcosis is a problem when breathing gases at high pressure. Typically, the maximum total partial pressure of narcotic gases used when planning technical diving can be around 4.5 bar absolute, based on an equivalent narcotic depth of 35 meters (114.8 ft). The effect of a Toxic pollutant such as carbon monoxide in the breathing gas is also related to the partial pressure when breathed. A mixture that may be relatively safe on the surface could be dangerously toxic at the maximum depth of a dive, or a tolerable level of carbon dioxide in a scuba rebreather's breathing loop can become intolerable within seconds of descent. when the partial pressure increases, and could lead to panic or incapacitation of the diver.
In medicine
Partial oxygen pressures in particular (pO2{displaystyle p_{mathrm {O}_{2}}}}) and carbon dioxide (pCO2{displaystyle p_{mathrm {CO}_{2}}}}) are important parameters in blood gas tests but can also be measured in, for example, cerebrospinal fluid.
| Unit | Arterial gastrics | Venous blood gas | Brain fluid | Alveolar lung gas pressures | |
|---|---|---|---|---|---|
| pO2{displaystyle p_{mathrm {O}_{2}}}} | kPa | 11–13 | 4.0–5,3 | 5.3-5.9 | 14,2 |
| mmHg | 75–100 | 30–40 | 40-44 | 107 | |
| pCO2{displaystyle p_{mathrm {CO}_{2}}}} | kPa | 4,7–6,0 | 5.5-6.8 | 5.9–6.7 | 4.8 |
| mmHg | 35–45 | 41-51 | 44–50 | 36 |
Contenido relacionado
Epididymis
Sarcoma
Medical diagnostic