Partial derivative

ImprimirCitar

In mathematics, the partial derivative of a function of several variables is the derivative with respect to each of those variables holding the others constant. Partial derivatives are used in vector calculus and differential geometry.

Partial derivative of a function ${displaystyle f(x,y,dots)}$ regarding the variable $x$ can be denoted in different ways:

{displaystyle {frac {partial f}{partial x}},{frac {partial }{partial x}}f,D_{1}f,partial _{x}f,f_{x}^{prime }{text{ o }}f_{x}.}

Where $partial$ is the rounded 'd' letter, known as the 'd of Jacobi'. It can also be represented as ${displaystyle D_{1}f(x_{1},x_{2},cdotsx_{n})}$ which is the first derivative regarding the variable ${displaystyle x_{1}}$ and so on. One of the first known uses of this symbol in mathematics is by the Marquis of Condorcet of 1770, who used it for partial differences. The modern notation of partial derivatives was created by Adrien-Marie Legendre (1786), but later abandoned it; Carl Gustav Jacobi reintroduced the symbol in 1841.

When a magnitude $A$ is function of various variables ( ${displaystyle x,y,z,...}$ ), that is to say:

{displaystyle A=fleft(x,y,z,...right)}

In performing this derivative we obtain the expression that allows us to calculate the slope of the tangent line to that function $A$ at a given point. This line is parallel to the plane formed by the axis of the unknown to which the derivative has been made with the axis that represents the values of the function.

Analytically, the gradient of a function is the maximum slope of that function in the chosen direction. While seen from linear algebra, the direction of the gradient indicates where there is greater variation in the function.

Introduction

Suppose $f$ is a function of more than one variable, that is, suppose $f$ is given by

{displaystyle z=f(x,y)=x^{2}+xy+y^{2}}

The graph of this function defines a surface in Euclidean space. For every point on this surface, there are an infinite number of tangent lines.

The chart of the

{displaystyle z=x^{2}+xy+y^{2}}

Partial derivation is the act of choosing one of those lines and finding its slope. Generally, the lines most interested are those that are parallel to the plane ${displaystyle xz}$ and those that are parallel to the plane ${displaystyle yz}$ .

Part of the chart in the plane

{displaystyle xz}

, in

{displaystyle y=1}

. The slope of the tangent line is

{displaystyle 3}

To find the slope of the tangent function line in ${displaystyle P(1,1)}$ parallel to the plane ${displaystyle xz}$ , we consider the variable $y$ as constant. The graphic of the function and this plane are displayed to the right. On the left, we see how the function looks on the plane ${displaystyle y=1}$ . Let's find the slope. $f$ at the point ${displaystyle (x,y)}$ deriving function $f$ considering $y$ as constant:

{displaystyle {frac {partial f}{partial x}}=2x+y}

So at the point ${displaystyle (1,1)}$ (replaced in the derivative) the slope is ${displaystyle 3}$ . This is, the partial derivative of $f$ with regard to $x$ at the point ${displaystyle (1,1)}$ That's it. ${displaystyle 3}$ as shown in the chart.

Definition

Formal definition

Analogously to the ordinary derivative (function of a real variable), the partial derivative is defined as a limit.

Sea $U$ is an open subset $mathbb {R} ^{n}$ and ${displaystyle f:Uto mathbb {R} }$ a function, the partial derivative $f$ at the point ${displaystyle mathbf {a} =(a_{1},dotsa_{n})in U}$ with regard to the $i$ - a variable $x_{i}$ defined as

{displaystyle {frac {partial }{partial x_{i}}}f(mathbf {a})=lim _{hrightarrow 0}{f(a_{1},dotsa_{i-1},a_{i}+h,a_{i+1},dotsa_{n})-f(a_{1},dotsa_{n}) over h}}

if the limit exists.

Even if all partial derivatives exist at the point ${mathbf {a}}$ , function is not necessarily continuous at that point. However, if all partial derivatives exist in an environment of ${mathbf {a}}$ and are continuous, then the function $f$ is totally different in that environment and the total derivative is continuous. In this case, it is said that $f$ It's a function. ${displaystyle C^{1}}$ .

The partial derivative

{displaystyle {frac {partial f}{partial x}}}

can be seen as another defined function on ${displaystyle U}$ and it can be derived again in part. If all mixed partial derivatives of second order are continuous at one point, then $f$ It's a function. ${displaystyle C^{2}}$ at that point; in such a case, partial derivatives can be exchanged by the Clairaut theorem:

{displaystyle {frac {partial ^{2}f}{partial x_{i}partial x_{j}}}={frac {partial ^{2}f}{partial x_{j}partial x_{i}}}}

Example

The volume of a cone depends on height (h) and radio (r)

Geometry

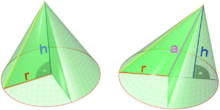
The volume $V$ of a cone that depends on the height of the cone $h$ and his radio $r$ , is given by the formula

{displaystyle V(r,h)={frac {pi r^{2}h}{3}}}

Partial derivatives of $V$ concerning $r$ and $h$ They are.

{displaystyle {begin{aligned}{frac {partial V}{partial r}}&={frac {2pi rh}{3}}\{frac {partial V}{partial h}}&={frac {pi r^{2}}{3}}end{aligned}}}

respectively, the first one represents the rate at which the volume of the cone changes if the radius varies and its height remains constant, the second one represents the rate at which the volume changes if the height varies and its radius remains constant.

Total derivative $V$ with regard to $r$ and $h$ They are.

{displaystyle {frac {dV}{dr}}=underbrace {frac {2pi rh}{3}} _{frac {partial V}{partial r}}+underbrace {frac {pi r^{2}}{3}} _{frac {partial V}{partial h}}{frac {dh}{dr}}}

and

{displaystyle {frac {dV}{dh}}=underbrace {frac {pi r^{2}}{3}} _{frac {partial V}{partial h}}+underbrace {frac {2pi rh}{3}} _{frac {partial V}{partial r}}{frac {dr}{dh}}}

respectively.

Gradient

Main article: Gradient

An important example of a function of several variables is the case of a function of scale f(x₁,... x_n) in a domain in the Euclidean space $mathbb {R} ^{n}$ (for example, in $mathbb{R} ^{2}$ or $mathbb{R} ^{3}$ ). In this case f has a partial derivative ▪f/▪x_j with respect to each variable x_j. At the point a, these partial derivatives define the vector

{displaystyle nabla f(a)=left({frac {partial f}{partial x_{1}}}(a),ldots{frac {partial f}{partial x_{n}}}(a)right).}

This vector is called the gradient from f into a. If f is differentiable at every point in some domain, then the gradient is a vector function ∇f that maps the point a to the vector ∇f(a). Consequently, the gradient produces a vector field.

An abuse of common notation is to define the operator of (post) as follows in three-dimensional euclidian space $mathbb{R} ^{3}$ with unit vectors ${displaystyle {hat {mathbf {i} }},{hat {mathbf {j} }},{hat {mathbf {k} }}}$ :

{displaystyle nabla =left[{frac {partial }{partial x}}right]{hat {mathbf {i} }}+left[{frac {partial }{partial y}}right]{hat {mathbf {j} }}+left[{frac {partial }{partial z}}right]{hat {mathbf {k} }}}

Or, more generally, for Euclidean space n- dimensional. $mathbb {R} ^{n}$ with coordinates ${displaystyle x_{1},ldotsx_{n}}$ and unitary vectors ${displaystyle {hat {mathbf {e} }}_{1},ldots{hat {mathbf {e} }}_{n}}$ :

{displaystyle nabla =sum _{j=1}^{n}left[{frac {partial }{partial x_{j}}}right]{hat {mathbf {e} }}_{j}=left[{frac {partial }{partial x_{1}}}right]{hat {mathbf {e} }}_{1}+left[{frac {partial }{partial x_{2}}}right]{hat {mathbf {e} }}_{2}+dots +left[{frac {partial }{partial x_{n}}}right]{hat {mathbf {e} }}_{n}}

Notation

Consider a function

{displaystyle {begin{aligned}f:mathbb {R} ^{3}&to mathbb {R} \(x,y,z)&mapsto f(x,y,z)end{aligned}}}

Partial derivatives of first order regarding the variable $x$ They tend to score.

{displaystyle {frac {partial f}{partial x}}=f_{x}=partial _{x}f}

Second-order partial derivatives are often denoted by

{displaystyle {frac {partial ^{2}f}{partial x^{2}}}=f_{xx}=partial _{xx}f=partial _{x}^{2}f}

The second-order cross derivatives by

{displaystyle {frac {partial ^{2}f}{partial ypartial x}}={frac {partial }{partial y}}left({frac {partial f}{partial x}}right)=f_{xy}=partial _{yx}f=partial _{y}partial _{x}f}

Thermodynamics

In thermodynamics and other areas of physics the following notation is used:

{displaystyle left({frac {partial Y}{partial X}}right)_{Z}}

Which means ${displaystyle exists f_{XZ}(cdot): Y=f_{XZ}(X,Z),}$ and then:

{displaystyle left({frac {partial Y}{partial X}}right)_{Z}:={frac {partial f_{XZ}(X,Z)}{partial X}}}

This notation is used because frequently a magnitude can be expressed as a function of different variables, so in general:

{displaystyle left({frac {partial Y}{partial X}}right)_{Z_{1}}neq left({frac {partial Y}{partial X}}right)_{Z_{2}}}

Since the precise form of functions ${displaystyle f_{XZ_{1}}(cdotcdot)}$ and ${displaystyle f_{XZ_{2}}(cdotcdot)}$ is different, that is, it is different functions.

Higher-order partial derivatives

In turn, the partial derivative ${displaystyle partial _{x_{i}}f}$ can be seen as another function defined in U and partly drift. If all their partial derivatives exist and are continuous, we call f a function C²; in this case, partial derivatives (called partial) can be exchanged by the Clairaut theorem also known as Schwarz theorem.

{displaystyle {frac {partial ^{2}f}{partial x_{i},partial x_{j}}}={frac {partial ^{2}f}{partial x_{j},partial x_{i}}}.}

In $mathbb {R} ^{2}$ If you comply with the above, you will ensure that:

{displaystyle {frac {partial ^{2}f}{partial x,partial y}}={frac {partial ^{2}f}{partial y,partial x}}=f_{xy}=f_{yx}}

Contenido relacionado

Más resultados...