Parallelism (mathematics)
In geometry parallelism is a relationship that is established between any linear variety of size greater or equal to 1 (recipes, planes, hyperplanes among others). In the Cartesian plane two straights are parallel if they have the same slope or are perpendicular to one of the axes, for example the constant function. In aphin geometry, expressing a linear variety as V = P + E, with p point and E vector space, it is said that A = a + F parallel to B = b + g Yeah. F is contained in G or G is contained in FWhere A and B are linear subvaries of the same linear variety V and F and G are vectorial subspaces of the same vector space E. At the level (floor) (V = R2{displaystyle mathbb {R} ^{2}}), this translates as follows: two straights are parallel if they contain the same director vector.
Note that, in a three-dimensional affine space, a line and a plane can be parallel, and also that the coincidence of linear manifolds is a particular case of parallelism.
Thus, two lines, contained in a plane, are parallel if, either they are one and the same line (they are coincident lines) or, on the contrary, they do not share any point.
Similarly, in space two planes are parallel if they are either one and the same plane, or they share no lines.
History
The definition of parallel lines as a pair of straight lines in a plane that do not meet appears as Definition 23 in Book I of Euclid's Elements. Other alternative definitions were discussed by other Greeks, often as part of a discussion. attempt to prove the parallel postulate. Proclus attributes a definition of parallel lines as equidistant lines to Posidonius and quotes Gemius in a similar vein. Simplicio also mentions the definition of Posidonius as well as its modification by the philosopher Aganis.
At the end of the 19th century in England, Euclid's Elements was still the standard textbook in schools high schools. The traditional treatment of geometry was being pressured to change by new developments in projective geometry and non-Euclidean geometry, so several new textbooks for teaching geometry were written around this time. An important difference between these reform texts, both among themselves and between them and Euclid, is the treatment of parallel lines. These reform texts were not without their critics and one of them, Charles Dodgson (a.k.a. Lewis Carroll), wrote a work, Euclid and his modern rivals, in which he attacks these texts.
One of the earliest Reformation textbooks was James Maurice Wilson's Elementary Geometry, from 1868. Wilson based his definition of parallel lines on the primitive notion of direction. According to Wilhelm Killing the idea can be traced back to Leibniz. Wilson, without defining direction as it is a primitive, uses the term in other definitions such as his sixth definition, "Two lines meeting each other have different directions, and the difference of their directions is the angle between them." Wilson (1868, p. 2) In definition 15 he introduces the parallel lines in this way; "Straight lines that have the same direction, but are not parts of the same straight line, are called parallel lines." Wilson (1868, p. 12) Augustus De Morgan reviewed this text and declared it a failure, primarily on the basis of this definition and the way Wilson used it to prove things about parallel lines. Dodgson also devotes a large section of his play (Act II, Scene VI § 1) to denouncing Wilson's treatment of parallels. Wilson edited this concept out of the third and superior editions of his text.
Other properties, proposed by other reformers, used as substitutes for the definition of parallel lines, did not fare much better. The main difficulty, as Dodgson pointed out, was that to use them in this way it was necessary to add additional axioms to the system. The definition of the equidistant line of Posidonius, expounded by Francis Cuthbertson in his 1874 text Euclidean Geometry, suffers from the problem that it is necessary to prove that points that are at a certain distance on one side of a line straight form a straight line. This cannot be proved and must be assumed to be true. The property of corresponding angles formed by a transversal, used by W. D. Cooley in his 1860 text, The Elements of Geometry, simplified and explained requires a proof of the fact that if a transversal meets a pair of lines at congruent corresponding angles then all transversals must. Again, a new axiom is needed to justify this claim.
Parallel lines
Two lines are parallel if their direction vectors are parallel, that is, if they never meet or cross.
Axiom of uniqueness
The axiom that distinguishes Euclidean geometry from other geometries is the following:
- On a plane, by an outside point to a straight line, it passes one and only one parallel to that straight.
Properties
Given the set P of straight in the plane, we can define the binary relationship: {displaystyle parallel } which we represent as follows:
- a b, (a,b),(a,b)한 한 {displaystyle aparallel bquadquad parallel (a,b)quadquad (a,b)in parallel }
If a, b, c are lines in the plane P, the following holds:
- Reflective: All straight is parallel to itself:
- Русский Русский a한 한 P:a a{displaystyle forall ain P:quad aparallel a}
- Simetric: If one line is parallel to another, that is parallel to the first:
- Русский Русский a,b한 한 P:a bΔ Δ b a{displaystyle forall a,bin P:quad aparallel blongrightarrow quad bparallel a}
These two properties follow from the intersection of sets and do not depend on the axiom of uniqueness.
- Transitive: If one line is parallel to another, and in turn parallel to a third, the first one is parallel to the third:
- Русский Русский a,b,c한 한 P:(a b∧ ∧ b c)Δ Δ a c{displaystyle forall a,b,cin P:quad {Big (};aparallel b;bparallel c;{Big)}longrightarrow quad aparallel c}
Then the relation of parallelism between lines of the plane is an equivalence relation.
These same properties can be verified in the set of parallel planes in space.
Theorems
- On a plane two straights perpendicular to a third are parallel to each other.
- If on a plane a straight cut to another straight, then cut all the parallels of this.
The proofs of these two theorems and of the third property use the axiom of uniqueness.
Extension to non-Euclidean geometry
In non-Euclidean geometry, it is more common to speak of geodesics than of (straight) lines. A geodesic is the shortest path between two points of a given geometry. In physics it can be interpreted as the path that a particle follows if no force is applied to it. In non-Euclidean geometry (elliptic or hyperbolic geometry) the three Euclidean properties mentioned above are not equivalent and only the second one (Line m is in the same plane as line l but does not intersect l) is useful in non-Euclidean geometries, since it does not imply any measurement. In general geometry the above three properties give three different types of curves, equidistant curves, parallel geodesics and geodesics sharing a common perpendicular, respectively.
Hyperbolic Geometry
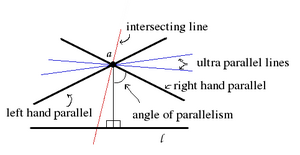
While in Euclidean geometry two geodesics can intersect or be parallel, in hyperbolic geometry there are three possibilities. Two geodesics that belong to the same plane can be:
- intersectingif you cross at a common point of the plane,
- parallel, if not crossed in the plane, but converge to a common limit point in the infinite (ideal point), or
- ultra parallelif they do not have a common limit point in infinity.
In the literature ultraparallel geodesics are often called non-intersecting. The geodesics that intersect at infinity are called limit parallels.
As in the illustration, through a point a that is not on line l there are two limit parallels, one for each ideal point direction of line l. They separate lines that intersect line l and lines that are ultra-parallel to line l.
Ultra-parallel lines have a unique common perpendicular (ultraparallel theorem), and they diverge on both sides of this common perpendicular.
Spherical or elliptical geometry
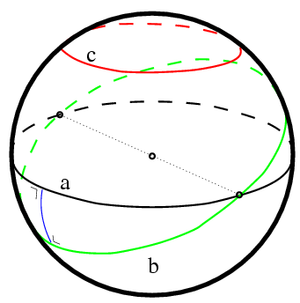
In spherical geometry, all geodesics are great circles. The great circles divide the sphere into two equal hemispheres, and all the great circles intersect each other. Therefore, there are no geodesics parallel to a given geodesic, since all geodesics intersect. Equidistant curves on the sphere are called parallels of latitude analogous to the lines of latitude on a globe. Parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center of the sphere.
Contenido relacionado
Continuous function
Exponential function
Stereographic projection