Parabola (mathematics)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Conical sections.

The path of a bounced ball is a succession of parables.

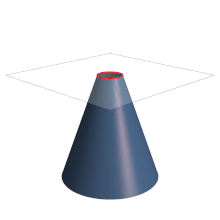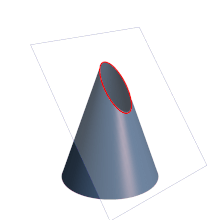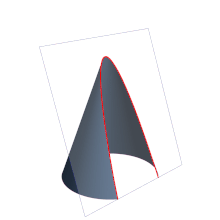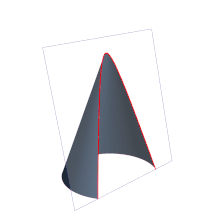
In mathematics, a parabola (from the Greek παραβολή) is the conic section with eccentricity equal to 1, resulting from cutting a right cone with a plane whose angle of inclination with respect to the axis of revolution of the cone is equal to that presented by its generatrix. The plane will therefore be parallel to said line. It is also defined as the locus of the points of a plane that are equidistant from a line called the directrix, and a point inside the parabola called the focus. In projective geometry, the parabola is defined as the enveloping curve of the lines that join pairs of homologous points in a similar or similar projectivity.

The parabola appears in many branches of applied sciences because its shape corresponds to the graphs of quadratic equations. For example, the ideal trajectories of bodies that move under the exclusive influence of gravity are parabolas (see parabolic motion and ballistic trajectory).

History

Tradition indicates that conic sections were discovered by Menechmus in his study of the problem of doubling the cube, where he proves the existence of a solution by cutting a parabola with a hyperbola, which is later confirmed by Proclus and Eratosthenes.

However, the first to use the term parable was Apollonius of Perge in his treatise Conics, considered a masterpiece on the subject of Greek mathematics, and where the study of tangents to conic sections is developed.

If a cone is cut by a plane through its axis, and is also cut by another plane that cuts the base of the cone in a straight line perpendicular to the base of the axial triangle, and if additionally the diameter of the section is parallel to one side of the axial triangle, then any straight line that is drawn from the section of a cone to its diameter parallel to the common section of the straight plane and one of the base And such a section will be called a parable.
Pole of Perge

It is Apolonio who mentions that a parabolic mirror reflects in parallel the rays emitted from its focus, a property used today in satellite antennas. The parabola was also studied by Archimedes, again in search of a solution to a famous problem: the squaring of the circle, resulting in the book On the squaring of the parabola.

Geometric properties

Different elements of a parable.

Diagram showing the reflective property, the guideline (green), and the lines that link the focus and the guideline of the parable (blue).

Although the identification of a parabola with the intersection between a right cone and a plane that forms an angle with the axis of revolution of the cone equal to that presented by its generatrix is exact, it is common to also define it as a locus:

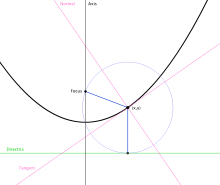
It is called parable to the geometric place of a point that moves on a plane in such a way that equidistant of a fixed line, called guideline and a fixed point in the plane, which does not belong to the parable or the guideline, called focus.

The definition excludes the case where the focus is on the guideline. In this way, once a straight and a point is fixed, a parable can be built that has them by guideline and focus respectively, using the following procedure: A point is taken $T$ any of the straight, joins it with the given focus $F$ and then traces the mediatrix (or perpendicular by the midpoint) of the segment ${displaystyle TF}$ . The intersection of the mediatrix with the perpendicular $T$ a guideline result in a point $P$ that belongs to the parable. Repeating the process for different points $T$ so many points of the parable can be found as necessary.

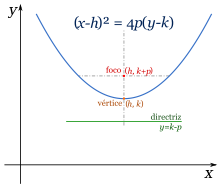
From the previous construction it can be proved that the parabola is symmetric with respect to the line perpendicular to the directrix that passes through the focus. The point of intersection of the parabola with such a line (known as the axis of the parabola) is called the vertex of the parabola and it is the point whose distance from the directrix is minimum. The distance between the vertex and the focus is known as the focal length or focal radius.

The points of the parable are at the same distance from the focus F and the guideline.

Construction of points in a parable.

Straight Side

The right side measures 4 times the focal distance.

The line segment included by the parabola, which passes through the focus and is parallel to the directrix, is known as straight side. Due to the equation that represents this curve, the following theorem arises:

The length of the right side is always 4 times the focal distance.

Being $D$ , $E$ the ends of the right side and $T$ , $U$ the respective projections on the guideline, denoting by $W$ the projection of the focus $F$ on the guideline, it is observed that ${displaystyle FEUW}$ and ${displaystyle DFWT}$ are square, and their sides measure ${displaystyle FW=2FV}$ . Therefore, the segment ${displaystyle DE}$ equals 4 times the segment ${displaystyle FV}$ (the focal distance).

The tangents to the parable that pass through the ends of the right side form 45° angles with the same, consequence of which ${displaystyle FEUW}$ and ${displaystyle DFWT}$ be square, along with the construction mentioned in the previous section. In addition, such tangents are cut in the guideline perpendicularly, precisely at the point of projection $W$ of focus, properties that can be used to build a geometric approach to focus and guideline when these are unknown.

Similarity of all parables

All parables are similar, it is only the scale that creates the appearance that they have different forms.

Since the parable is a conical section, it can also be described as the only conical section that has eccentricity. $e=1$ . Oneness refers to the fact that all parables are similar, that is, they have the same form, except their scale.

Unfortunately, when studying parabolas analytically (based on equations), it is often wrongly asserted that the parameters of the equation change the shape of the parabola, making it wider or narrower. The truth is that all parabolas have the same shape, but the scale creates the illusion that there are parabolas of different shapes.

An informal geometric argument is that since the directrix is an infinite line, when taking any point and carrying out the construction described above, the same curve is always obtained, except for its scale, which depends on the distance of the point from the directrix.

Tangents to the parabola

The tangent bis the angle between the focus, the point of tangence and its projection.

Use of the properties of tangents to build a parable through paper folds.

An important result regarding the tangents of a parabola states:

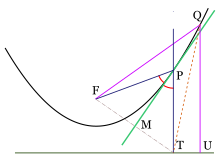
The tangent bis the angle between the focus, the point of tangence and its projection.

Call. F to the focus of a parable, $P$ to any point of the same and $T$ to the projection of this on the guideline. Sea ${displaystyle MP}$ the mediatrix of the triangle ${displaystyle FPT}$ , which is isosceles by being equal distances ${displaystyle FP}$ and ${displaystyle PT}$ as seen. Later. ${displaystyle MP}$ biseca at angle ${displaystyle FPT}$ by failing to verify if he is tangent to the parable at the pointP.

Sea Q another point in the parable and U his projection in the guideline. Post ${displaystyle FQ=QU}$ and $<math alttext="{displaystyle QUQU.QT{displaystyle QU ingredientQT} <img alt="{displaystyle QU$ , then $<math alttext="{displaystyle FQFQ.QT{displaystyle FQ ingredientQT} <img alt="{displaystyle FQ$ . Since this is true for any other point in the parable, it is concluded that the whole parable is on the same side of the parable. ${displaystyle MP}$ , and since inequality is strict, there is no other point in the parable that touches the straight ${displaystyle MP}$ , this means that ${displaystyle MP}$ is the tangent of the parable in $P$ .

Dual curve of the parabola.

The dual curve of the parabola with respect to an inner circle is an ellipse. If the center of the circle is the focus of the parabola then its dual is a circle. The dual of the parabola with respect to an outer circle is a hyperbola. If the center of the circle is on the parabola, its dual is another parabola.

Dual of the parable. Circle center inside the parable.
Dual of the parable. Circle center in the focus of the parable.
Dual of the parable. Circle center outside the parable.
Dual of the parable. Circle center on the parabola.

Radius of curvature

Be the point ${displaystyle M(x_{1},y_{1})}$ Then the curvature radius is

${displaystyle R={frac {(p+2x_{1})^{frac {3}{2}}}{sqrt {p}}}={frac {p}{sen^{3}u}}={frac {n^{3}}{p^{2}}}}$

being the equation of the parabola

${displaystyle y^{2}=2px}$ Where u is the slope of the tangent straight in M; n, normal length MN

Expressive expression

Given the general formula for the radius of curvature of a curve from its explicit equation:

{displaystyle R_{c}={frac {left[1+left({frac {df}{dx}}right)^{2}right]^{frac {3}{2}}}{left|{frac {d^{2}f}{dx^{2}}}rightvert }}}

if we have a parabola expressed in the general form:

{displaystyle y=Ax^{2}+Bx+C}

; its first derivative takes shape

{displaystyle y'=2Ax+B}

and its second derivative is

{displaystyle y''=2A}

Substituting these values in the previous general expression, we have:

${displaystyle R_{c}={frac {[1+(2Ax+B)^{2}]^{frac {3}{2}}}{2A}}}$
Curve in the vertex

In the vertex, where the tangent to the curve is horizontal, the first derivative of the parable is annulled (i.e., ${displaystyle (2Ax+B)=0}$ ). Accordingly,

{displaystyle R_{c}V={frac {1}{2A}}}

Practical applications

A consequence of great importance is that the tangent reflects the rays parallel to the axis of the parabola in the direction of the focus. The practical applications are many: satellite antennas and radio telescopes take advantage of the principle by concentrating signals received from a distant transmitter on a receiver placed at the focus position.

The concentration of solar radiation at a point, through a parabolic reflector, has its application in small solar cookers and large solar energy collecting plants.

Similarly, an emitting source located at the focus will send a beam of rays parallel to the axis: various lamps and headlights have mirrors with reflective parabolic surfaces to be able to send parallel beams of light emanating from a source in a focal position. The rays converge or diverge if the emitter is displaced from the focal position.

The parable reflects on the focus the parallel rays to the axis. Similarly, a emitter located in the focus will send a beam parallel to the axis.
Radiotelescopes concentrate signal beams on a receiver located in the focus. The same principle applies to a radar antenna.
Parabolic concentrator solar cooker. The same method is used in large solar power plants.
The lighthouses of the cars send parallel beams, if the bulb is placed in the focus of a parabolic surface.

Equations of a parabola

Parables type and = ax², with a = 4, 1, ¹♪₄ and ¹♪₁₀.

Geometric test of the relationship and=ax².

With the advent of analytical geometry began a study of geometric forms based on equations and coordinates.

A parable whose vertice is in the origin and its axis coincides with the axis of the ordained, has an equation of the form ${displaystyle y=ax^{2}}$ where the parameter $a$ specifies the scale of the parable, incorrectly described as the shape of the parable, since as was said before, all parables have the same form. When the parameter is positive, the parable opens “up” and when it is negative it opens “down”.

Although the expression in the form of an equation was not possible until the development of analytic geometry, the geometric relationship expressed in the above equation was already present in the works of Apollonius, and will be outlined below using modern notation.

Taking again the definition of parable as a section of a straight cone parallel to the directive, be it $V$ a point in the axis and ${displaystyle QV}$ perpendicular to the axis. ( ${displaystyle QV}$ corresponds to the value $x$ in the analytical version and ${displaystyle PV}$ value and). Considering the circular section passing through $Q$ and is parallel to the base of the cone, we get $H$ , $K$ parallel to $B$ and $C$ .

By the power of a point theorem:

$QV^2 = HVcdot VK$ .

Being ${displaystyle PM}$ parallel ${displaystyle AC}$ , triangles ${displaystyle HVP}$ , ${displaystyle HKA}$ and ${displaystyle BCA}$ They are similar and so:

$frac{HV}{PV} = frac{HK}{KA} = frac{BC}{AC}$ .

Using the parallels again:

$frac{VK}{PA} = frac{HK}{HA} = frac{BC}{BA}$ .

Clearing ${displaystyle HV}$ and ${displaystyle VK}$ to replace in the formula ${displaystyle QV^{2}}$ results

$QV^2=HVcdot VK=left(frac{BCcdot PV}{AC}right)left(frac{BCcdot PA}{BA}right) = left(frac{BC^2cdot PA}{BAcdot AC}right)PV$ .

But the value of $left(frac{BC^2cdot PA}{BAcdot AC}right)$ is a constant, because it does not depend on the position of $V$ , so doing

$a = frac{BAcdot AC}{BC^2cdot PA},$

throws the modern expression ${displaystyle y=ax^{2}}$ .

Vertical parables, with shape equations y=ax2+bx+c.

By applying a coordinate substitution we can now obtain the equation of a vertical parabola for any position of its vertex.

The equation of a parable whose axis is vertical and its vertice is ${displaystyle (u,v)}$ It has shape ${displaystyle (y-v)=a(x-u)^{2}}$ ,

grouping the terms and rearranging an equivalent form is obtained:

The equation of a parable whose axis is vertical is shaped $y = a x^2 + bx + c ,$ .

If the parabola is horizontal, similar equations are obtained, but exchanging y for x and vice versa. Thus we would have:

The equation of a parable whose axis is horizontal is shaped $x = a y^2 + by + c ,$ .

Equation involving focal length

Equation of a vertical parable.

There can be many parabolas that have the same vertex (varying the parameter a) in the first equation. However, given two fixed points, there is only one parabola that has them as vertex and focus, since the directrix is automatically fixed as the perpendicular to the line that joins the focus with the vertex and at the same distance from the latter.

Consider the special case in which the vertex is ${displaystyle (0,0)}$ and the focus is ${displaystyle (0,p)}$ . The guideline is therefore the horizontal line that passes through ${displaystyle (0,-p)}$ . At the distance between the vertex and the focus is called focal distanceso in this case the focal distance is equal to $p$ . With this configuration you have:

The equation of a parable with vertice in (0.0) and focus on (0,pIt is $,x^2=4py$ .

Alternately:

The equation of a parable with vertice in (0.0) and focus on (0,pIt is $y=frac{x^2}{4p}$ .

Note that the coefficient 4p is precisely the length of the straight side of the parabola.

Both equations refer to vertical parabolas that open "up". The equation of a parabola that opens downward is similar, except that a sign varies. In this case, the focus would be (0,-p) and thus:

The equation of a parable with vertice in (0.0) and focus on (0.-pIt is $,x^2=-4py$ .

When the parabola is horizontal "to the right", a similar equation is obtained by swapping the roles of x, y:

The equation of a parable with vertice in (0.0) and focus on (p,0) is $,y^2=4px$ ,

obtaining by a change of sign the equation of the parabolas to the left.

Finally, the equations when the vertex is not in the center are obtained by a translation. In the common case of the vertical parabola upwards we have

The equation of a parable with vertice in (h,k) and focus on (h,k + pIt is $,(x-h)^2=4p(y-k)$ ,

while for the horizontal parabola swap x with y:

The equation of a parable with vertice in (h,k) and focus on (h + p,kIt is $,(y-k)^2=4p(x-h)$ .

General equation of a parabola

The algebraic expression that describes a parable that occupies any position on a plane is:
${displaystyle ,ax^{2}+bxy+cy^{2}+dx+ey+f=0}$
Yes and only if
$,b^2 - 4ac = 0$
and coefficients a and c cannot be simultaneously null.

Through translations and rotations it is possible to find a reference system in which the previous equation is expressed by an algebraic formula of the form ${displaystyle ax'^{2}+bx'+c=0}$ Where a It's different from zero.

As trisector

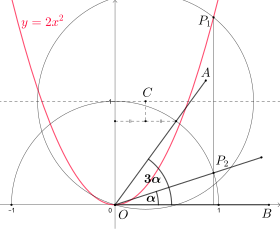
Trisection of an angle through a parable

The parabola can be used as a trisector, that is, it allows the exact trisection of an arbitrary angle to be carried out when used as an auxiliary means of a construction with a ruler and compass. This fact is not in contradiction with the impossibility of carrying out the trisection of an angle exclusively with a ruler and compass, since the use of parabolas is not allowed in the rules of constructions with a classical ruler and compass.

To trisecar ${displaystyle angle AOB}$ , place your cathet ${displaystyle OB}$ in the axis x so that the vertex $O$ is at the origin of the coordinate system. The coordinate system also contains the parable ${displaystyle y=2x^{2}}$ . The unit circle with radius 1 around the origin is crossed with the other angle caeto ${displaystyle OA}$ and, from this point of intersection, you should draw the perpendicular on the axis and. The parallel to the axis and that passes through the middle point of that perpendicular and tangent in the unit circle in ${displaystyle (0,1)}$ intersecting $C$ . The circle around $C$ with radio ${displaystyle OC}$ crosses with the parable in $P_1$ . The perpendicular $P_1$ axis x intersecting the unit circle in $P_2$ and ${displaystyle angle P_{2}OB}$ It's exactly a third of ${displaystyle angle AOB}$ .

The accuracy of this construction can be seen showing that the coordinate x of $P_1$ That's it. ${displaystyle cos(alpha)}$ . Solve the system of equations given by the circle around $C$ and the parable leads to the cubic equation ${displaystyle 4x^{3}-3x-cos(3alpha)=0}$ . The Triple Angle Formula ${displaystyle cos(3alpha)=4cos(alpha)^{3}-3cos(alpha)}$ allows to prove that ${displaystyle cos(alpha)}$ is in fact a solution to that cubic equation.

This trisection dates back to René Descartes, who described it in his book La Géométrie (1637).

Contenido relacionado

Más resultados...