Orthocenter

The triangle abc is the ortic triangle of the triangle ABC.

The orthocenter is the point where the three lines that contain the three heights of a triangle intersect.

The name derives from the Greek term ortho, which means straight, referring to the angle formed between the bases and the heights.

The orthocenter is inside the triangle if it is acute; coincides with the vertex of the right angle if it is right, and is on the outside of the triangle if it is obtuse.

Orthic triangle

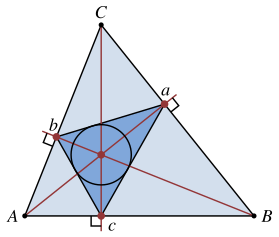
Given any triangle (excluding a right triangle), the 'orthic triangle or pedal triangle with respect to the given, is the one whose vertices are the feet of the three heights of this, that is, the projections of the vertices on the sides.

• The orthocentre of an acutaneous triangle is the incenter of its ortic triangle (as seen in the figure).

• The heights of a triangle are the bisectrices of the angles of the pedal triangle.

• In the case of a rectangle triangle, the vertex of the right angle, which with the foot on the hypotenuse, at most, form a segment, in this case there is no pedal triangle.