Orbital period

Image of trace of rays that shows the concepts of inclination, length of the ascending node and argument of the periapsis of a "menor" object in an elliptical orbit around a larger object.

The orbital period is the time it takes a star to complete its orbit. When it comes to objects that orbit around the sun there are two types:

• The period is the time that takes the object to take a complete spin around the sun, taking as a reference point a fixed star. It is considered the authentic orbital period of the object and would be the one who would see a still observer who would not orbit around the sun.
• The Synod period It is the time it takes for the object to re-appear at the same point in the sky regarding the sun, when it is observed from the Earth. This period takes into account that the Earth, where the object is observed, also orbits around the sun. It is, therefore, the time between two successive conjunctions with the sun, and it is the apparent orbital period.

The sidereal period and the synodic period differ since the Earth, in turn, revolves around the Sun.

Other periods related to the orbital period

There are many periods associated with the orbits of objects, each of which are often used in the various fields of astronomy and astrophysics. Examples of some of the most common are:

The sidereal period is the amount of time it takes an object to make a complete orbit, relative to the stars. This is the orbital period in an inertial (non-rotating) frame of reference.

The synodic period is the amount of time it takes for an object to reappear at the same point in relation to two or more objects (for example, the phase of the Moon and its position relative to the Sun and the Earth repeat every 29.5 synodic days, longer than its 27.3-day orbit around the Earth, due to the movement of the Earth around the Sun). The time between two successive oppositions or conjunctions is also an example of a synodic period. For the planets of the solar system, the synodic period (with respect to the Earth) differs from the sidereal period due to the Earth's orbit around the Sun.

The draconian period or draconic period is the time between two passages of the object through its ascending node, the point in its orbit where it crosses the ecliptic from the southern hemisphere to the northern hemisphere. This period differs from the sidereal period because both the orbital plane of the object and the plane of the ecliptic precess are separated with respect to the fixed stars, so their intersection, the line of nodes, also precesses with respect to the fixed stars. Although the ecliptic plane often remains fixed at the position it occupied at a specific epoch, the object's orbital plane still precesses causing the draconitic period to differ from the sidereal period.

The anomalistic period is the time that elapses between two passages of an object in its periapsis (in the case of the planets of the solar system, called perihelion), the point of its closest approach to the attractive body. It differs from the sidereal period because the semi-major axis of the object tends to move slowly.

In addition, the tropical period of the Earth (or simply its "year") is the time that elapses between two alignments of its axis of rotation with the Sun, also seen as two passages of the object in zero right ascension. An Earth year has a slightly shorter interval than the solar orbit (sidereal period) because the inclined axis and equatorial plane slowly advance (rotate with respect to the stars), realigning with the Sun before the orbit is complete. The Earth's precession cycle is completed in about 25,770 years.

Standard calculation of orbital period

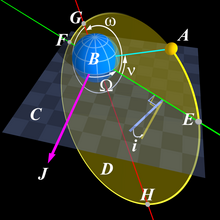
A small body orbiting a central body

The major semieje (a) and the minor semieje (b) of an ellipse.

Period recording chart (T) against semi-major axis (a). The 3/2 slope shows that T a a^3/2.

Given a circular or elliptical orbit around a massive central object, Kepler's third law, the orbital period T (in seconds) Is given by:

T=2π π a3μ μ {displaystyle T=2pi {sqrt {frac {a^{3}}{mu }}}}}}

where:

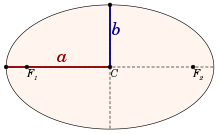
• a{displaystyle a} is the larger semi-axis of the orbit (in meters).
• μ μ =GM{displaystyle mu =GM}is the standard gravitational parameter in m3 s^-2
  • G It's the gravitational constant. G=6.674⋅ ⋅ 10− − 11m3kg− − 1s− − 2{displaystyle G=6.674cdot 10^{-11} m^{3}kg^{-1s}^{-2}.
  • M is the mass of the most massive object.

Note that this period is valid for all closed orbits, that is, circular and elliptical, regardless of their eccentricity.

Inversely we can calculate the semi-major axis of an orbit given its orbital period with the following expression:

a=μ μ T24π π 23=GMT24π π 23{displaystyle a={sqrt[{3}]{frac {mu T^{2}{4pi ^{2}}}}}}}{sqrt[{3}]{frac {GMT^{2}}{4pi ^{2}}}}}}}{

We could, for example, calculate a curious case that is not very viable in practice. If we wanted to orbit a light object with a mass of 100 kg with a period of 24 hours in a circular orbit, its radius should be 1.08 meters.

Two bodies orbiting each other

In celestial mechanics, when the masses of both orbiting bodies have to be taken into account, the orbital period T can be calculated as follows:

T=2π π a3G(M1+M2){displaystyle T=2pi {sqrt {frac {a^{3}}{Gleft(M_{1}+M_{2}right}}}}}}}}}}}

where:

• a is the sum of the semi-major axes of the ellipses in which the centers of the bodies are moved, or equivalent, the semi-major axis of the ellipse in which a body is moved, in the frame of reference with the other body in the origin (which is equal to its constant separation for circular orbits),
• M₁ + M₂ is the sum of the masses of the two bodies,
• G It's the gravitational constant.

Note that the orbital period is independent of size: for a scale model it would be the same, when the densities are the same (see also Orbit § Scaling in gravity).

In a parabolic or hyperbolic trajectory, the motion is not periodic, and the duration of the complete trajectory is infinite.

Calculation of the sidereal period

Assuming completely circular orbits, the Earth would move 360° in a time T of 365.2425 days, while the body would move 360° in a time P (sidereal or real period). That's equal to S time (synodic or apparent period) plus an offset for going faster or slower than Earth. Therefore, the following equation is obtained:

(360gradorsP)⋅ ⋅ S=(360gradorsT)⋅ ⋅ S± ± 360gradors{displaystyle left({360grades over P}right)cdot S=left({360grades over T}right)cdot Spm 360grades}

The sign of ±360° is a sum if the body turns its orbit in less time than the Earth —be it an inner planet (other than Mars or the Earth itself) or the Moon—, it is a subtraction if the star goes around its orbit in a longer time than the Earth —be it Mars, an outer planet or a dwarf planet.

Simplifying and clearing, using algebra, we obtain the following formula:

1P=1T± ± 1S{displaystyle {1 over P}={1 over T}pm {1 over S}}

From which if we clear the synodic period S we obtain this as a function of the sidereal periods of the Earth T and the planet P

S=T⋅ ⋅ P日本語P− − T日本語{displaystyle S={dfrac {Tcdot P}{vert P-Tvert }}}}

The synodic periods of the 7 planets are: 115.88 days for Mercury, 583.92 days for Venus, 779.94 days for Mars, 398.88 days for Jupiter, 378.09 for Saturn, 369.66 days for Uranus and 367.49 days Neptune.

And if what we want to calculate is the sidereal period P of the planet given its synodic period S and the sidereal period of the Earth T the expression is:

P=T⋅ ⋅ S日本語S− − T日本語{displaystyle P={dfrac {Tcdot S}{vert S-Tvert }}}}

Checking

To check the validity of the calculation of the sidereal period from the synodic period we will use a real case: the Moon. If we are on Earth and we observe the moon through the days we will see that it takes approximately 29 d 12 h 44 min in its synodic period (apparent from Earth with respect to the sun) or 29.530556 days, which is the value of S. We know that the Earth takes approximately 365.256363 days to go around the sun, which will be our T value. The operation looks like this:

1P=1365.256363+129.530556=0.036601{displaystyle {1 over P}={1 over 365.2563}+{1 over 29.530556}=0.036601}

The sign is positive since it goes around its own orbit faster than Earth does. The result is rounded to six decimal places. It is the value of 1/P and to obtain P (sidereal or real period, of the moon in this case) we only do the operation 1÷0.036601 = 27.321659 days.

We know that the sidereal period of the moon is approximately 27 d 7 h 43 min or 27.321529 days, so our result is very close to the true value.