Number

Multiple bingo chips showing different numbers.

A Numberis an abstract concept used to count (cantities), measure (magnitudes) and label. The simplest numbers, which we all use in everyday life, are the natural numbers: 1, 2, 3, etc. They are denoted by N{displaystyle mathbb {N} } and also serve as ordinales, to establish an order (first, second,...). Sometimes we use the term Number to talk about what is actually a numeral or number (e.g. our Arabic numerals). From a totally general point of view a number is any element of a logical-mathematic structure known as a numerical system.

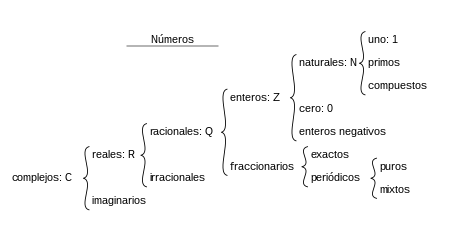
The numbers play a fundamental role in the empirical sciences; not only the natural ones, but many other numbers that contemplate mathematics. The whole set of numbers (represented by Z{displaystyle mathbb {Z} }) is an extension of the natural ones, including the negatives (we use to represent debts, and in the thermometers for temperatures below zero). If we include fractional numbers (1/3, 0,75, -3,25, etc.) you get the set of rational numbers, whose symbol is Q{displaystyle mathbb {Q} }. Already in ancient times it was discovered that there are unreasonable numbers: the diagonal of a square side 1 mide root of two, a number that cannot be represented as an integer or as a fraction; it is irrational. The rationals together with the irrationals form the set of the actual numbers, (R). Later, other types of numbers have been added: imaginary, transcendent, unreal, complex,...

Note that number theory is a branch of mathematics that deals with integers (not numbers in general).

Types of numbers

Classification of numbers.

The most known numbers are natural numbers. Denotated by N{displaystyle mathbb {N} }, are conceptually the simplest and most used to count discreet units. These, together with the "negative" numbers, make up the whole, denotated by Z{displaystyle mathbb {Z} } (German) Zahlen, ‘numbers’). Negative natural numbers formally represent debts, and generalize the subtraction of any two natural numbers. I mean, we already have a solution for operations like, for example, 3-2 = 1.

Another type of widely used numbers are fractional numbers, which represent both quantities below one unit, and mixed numbers (a set of units plus a lower part of the unit). Fractionary numbers can always be expressed as quotients of integers. The set of all fractional numbers is the set of rational numbers (which is usually defined to include both the positive rationals, the negative rationals and zero). This set of numbers is designated as Q{displaystyle mathbb {Q} }. As with the integers you can calculate the result of any subtraction, with the rationals it is possible to make divisions that have no whole result, such as 15/2 = 7.5 or 71⁄2.

The rational numbers allow to solve a lot of practical problems, but from the ancient Greeks it is known that certain geometric relationships (the diagonal of a square side unit) are not integer numbers that are not rational either. Likewise, the numerical solution of a polynomial equation whose coefficients are rational numbers is usually a non-sound number. It can be shown that any irrational number can be represented as a Cauchy succession of rational numbers that approach a numerical limit. The set of all rational and irrational numbers (obtained as limits of Cauchy successions of rational numbers) is the set of real numbers R{displaystyle mathbb {R} }. For a while it was thought that any existing physical magnitude could be expressed in terms of actual numbers exclusively. Among the real ones, there are numbers that are not solutions of a polynomial or algebraic equation, and they receive the name of transcendentals. The best known of these numbers are the number π (Pi) and the number e (this last base of the natural logarithms), which are interrelated by the identity of Euler.

One of the problems of real numbers is that they do not form an algebraicly closed body, so certain problems have no solution raised in terms of real numbers. That is one of the reasons why complex numbers were introduced C{displaystyle mathbb {C} }, which are the minimum algebraicly closed body that contains the actual numbers. In addition, in some practical applications, as well as in standard quantum mechanic formulations it is considered useful to introduce complex numbers. Apparently, the mathematical structure of complex numbers reflects existing structures in physical problems, so in theoretical physics and in various applications complex numbers are used on an equal footing with real numbers, even though they were initially considered only as a mathematical artifice without relation to physical reality. All sets of numbers N,Z,Q,R,C{displaystyle mathbb {N}mathbb {Z}mathbb {Q}mathbb {R}mathbb {C} } they were somehow "discovered" or suggested in connection with problems raised in physical problems or within elementary mathematics and they all seem to have important connections with physical reality.

Apart from real and complex numbers, clearly connected to problems in the natural sciences, there are other types of numbers that further generalize and extend the concept of number in a more abstract way and are more responsive to deliberate creations by mathematicians. Most of these generalizations of the number concept are used only in mathematics, although some of them have found applications in solving certain physical problems. Among them are hypercomplex numbers, which include quaternions, useful for representing rotations in a three-dimensional space, and generalizations of these, such as octonions and sedenions.

At a somewhat more abstract level, sets of numbers capable of dealing with infinite and infinitesimal quantities, such as hyperreals, have also been devised. ↓ ↓ R{displaystyle} {^{mathbb {R} } and transfinites. And equally the rational numbers can be extended in other ways, as by axis to form the p-addic numbers, among which are the p-addic integers. Zp{displaystyle mathbb {Z} _{p}}the p-addic rationals Qp{displaystyle mathbb {Q} _{p}} or the p-addic complexes Ω Ω =Cp{displaystyle Omega =mathbb {C} _{p}}that satisfy Zp Qp Cp{displaystyle mathbb {Z} _{p}subset mathbb {Q} _{p}subset mathbb {C} _{p}}}.

List of existing number types

Number theory basically deals with the properties of natural numbers and integers, while the operations of algebra and calculus make it possible to define most of the number systems, among which are:

Structure of number systems

In abstract algebra and mathematical analysis a number system is characterized by a:

• Algebraic structure, usually a commutative ring or mathematical body (in the case not commutative are an algebra on a body and in the case of natural numbers only a commutative monoid).
• Structure of order, usually an ordained set, in the case of natural, integer, rational and real numbers are totally ordained sets, although complex and hypercomplete numbers are only partially ordained assemblies. The real ones are also a well ordered set and with a dense order.
• Topological structure, numberable numerical sets are usually discrete sets, on which discreet topology is considered, while on non-numberable sets it is considered a topology that makes them suitable for mathematical analysis.

Another interesting property of many numerical sets is that they can be represented by Hasse diagrams, Euler diagrams and Venn diagrams, being able to take a combination of both in an Euler-Venn diagram with the characteristic shape of a quadrilateral and also being able to represent internally a Hasse diagram (it is a straight line). Both historically and conceptually, the various numerical sets, from the simplest of natural numbers, to transcendental extensions of real and complex numbers, elaborated through model theory during the XX, build from a simpler structure to a more complex one.

Special natural numbers

The study of certain properties of numbers has produced an enormous number of types of numbers, most of which are of no specific mathematical interest. They can be framed within recreational mathematics. Here are a few:

• Perfect: number equals the sum of its dividers (including 1). Example: 6 = 1 + 2 + 3.
• Sheldon: number 73, is the 21st prime number, which by multiplying 7 x 3 = 21; and by turning to their digits it gives 37 that is the 12th prime number.
• Narcissist: number of n digits that turns out to be equal to the sum of the powers of order n of their digits. Example: 153 = 13 + 53 + 33.
• Omirp: prime number that when you invest your digits gives another prime number. Example: 1597 and 7951 are cousins.
• Vampire: number that is the product of two numbers obtained from their digits. Example: 2187 = 27 x 81.
• Hamsteriano: Its arithmetic structure N= (a×b)²-1 where a and b are the two cousins, the sum of their divisors surpasses N, and the number of their divisors is  a×b/2; it goes as example: 1224 = (5×7)²-1
• Pythagorean: a pythagorean tenare are three numbers that meet the following conditions: the square of one of them, plus the square of another, is equal to the square of the third, for example: (3, 4, 5) since 3² + 4² = 9 + 16 = 25 = 5²

Once the problem of the nature and classification of numbers is understood, another one arises, more practical, but which conditions everything that is going to be done with them: the way to write them. The system that has been universally imposed is positional numbering, thanks to the invention of zero, with a constant base.

More formally, in The Fundamentals of Arithmetic, Gottlob Frege gives a definition of «number», which was taken as a reference by many mathematicians (among them Bertrand Russell, co-creator of mathematical principle):

“n” is a number, then it is the definition of “that there is a “F” concept for which “n” applies”, which in turn is explained as “n” is the extension of the concept “equinumerable with” for “F”, and two concepts are equalified if there is a “one to one” relationship (see that the “1” symbol is not used because it is not yet defined) among the elements that make it a bisection.

Note also that Frege, as much as any other mathematician, finds himself unable to define number as the expression of a quantity, because mathematical symbology does not necessarily refer to numerability, and the fact of «quantity» would refer to something countable, while numbers are adopted to define the cardinality of, for example, the elements that lie in the open interval (0, 1), which contains innumerable elements (the continuum).

Peano, before establishing his five propositions on the natural numbers, explicitly states that a definition is known (perhaps due to its «obviousness») of the words or concepts zero, successor and number. In this way he postulates:

• 0 is a natural number
• the successor of every number is a number
• two different numbers do not have the same successor
• 0 is not the successor of any number
• and inductive property

However, if one defines the concept zero as the number 100, and the concept number as the numbers greater than 100, then the five propositions mentioned above apply, not to the idea that Peano would have wanted to communicate, but to its formalization.

The definition of number is therefore not fully formalized, although there is a majority agreement in adopting the definition enunciated by Frege.

History of the concept of number

Ishango's bone.

Cognitively, the concept of number is associated with the ability to count and compare which of two sets of similar entities has the greatest number of elements. The first human societies were very soon faced with the problem of determining which of two sets was "greater" than the other, or of knowing precisely how many elements made up a collection of things. Those problems could be solved simply by counting. The human being's ability to count is not a simple phenomenon, although most cultures have counting systems that reach at least hundreds, some peoples with a simple material culture only have terms for the numbers 1, 2 and 3. and they usually use the term "many" for larger quantities, although when necessary they recursively use translatable expressions such as "3 plus 3 and 3 others".

The count must have been initiated through the use of physical objects (such as piles of stones) and tally marks, such as those found on carved bones: Lebombo's, with 29 notches etched into a baboon bone, has about 37,000 years old and another wolf bone found in former Czechoslovakia, with 57 marks arranged in five groups of 11 and two loose, has been estimated to be about 30,000 years old. Both cases constitute one of the oldest known count marks, having been suggested that they could be related to records of lunar phases. Regarding the ordinal origin, some theories place it in religious rituals. The numeral systems of most linguistic families reflect that the counting operation was associated with finger counting (which is why the decimal and vigesimal base systems are the most abundant), although the use of other numeral bases has been attested.

The move towards numeral symbols, like writing, has been associated with the appearance of complex societies with centralized institutions constituting bureaucratic accounting artifices in tax and property records. Its origin would be in primitive symbols with different shapes for the counting of different types of goods such as those found in Mesopotamia inscribed on clay tablets that in turn had come to progressively replace the counting of different goods with clay tokens (confirmed at least since 8000 BC) The oldest numeral symbols found are located in the Mesopotamian civilizations, being used as a numeral system not only for accounting or commerce but also for surveying or astronomy, such as records of planetary movements.

Overall, for 5000 years most civilizations have counted as we do today although the way of writing the numbers (although they all represent with accuracy of natural ones) has been very diverse. Basically we can classify it into three categories:

1. Additive notation systems. They match the symbols of all units, dozens, hundreds,..., necessary until the number is complete. Although symbols can go in any order, they always adopted a certain position (more than less). Of this type are the numbering systems: Egyptian, Hittite, Cretan, Roman, Greek, Armenian and Jewish.
2. Hybrid Notation Systems. They combine the additive principle with the multiplier. In the previous 500 is represented with 5 symbols of 100, in these the combination of 5 and 100 is used. The order of the figures is now fundamental (we are one step away from the positional system). Of this type are the numbering systems: Classic Chinese, Assyrian, Armenian, Ethiopian and Maya. The latter used symbols for 1, 5 and 0. This being the first documented use of the zero as we know it today (36 BC) as the one of the Babylonians was only used among other digits.
3. Positioning notation systems. The position of the figures indicates whether they are units, dozens, hundreds,..., or generally the power of the base. Only three cultures besides the Indian managed to develop such a system: The Chinese system (300 B.C.) that did not have 0, the Babylonian system (2000 B.C.) with two symbols, base 10 additive up to 60 and positional (based 60) onwards, with 0 up to 300 B. C.

Egyptian Unit Fractions (Ahmes/Rhind Papyrus)

In this papyrus acquired by Henry Rhind in 1858 whose content dates from 2000 to 1800 B.C. in addition to the numbering system described above we find his treatment of the fractions. They do not consider the fractions in general, only the unitary fractions (verses of the natural 1/20) that are represented with an oval sign above the number, the fraction 2/3 that is represented with a special sign and in some cases fractions of the type n/n+1{displaystyle n/n+1}. There are breakdown tables 2/n{displaystyle 2/n} from n=1 to n=101, for example 2/5=1/3+1/15{displaystyle 2/5=1/3+1/15} or 2/7=1/4+1/28{displaystyle 2/7=1/4+1/28}We don't know why they didn't use 2/n=1/n+1/n{displaystyle 2/n=1/n+1/n} but they seem to be trying to use smaller unit fractions than 1/n{displaystyle 1/n}.

Being a summative system, the notation is: 1+1/2+1/4. The fundamental operation is addition and our multiplications and divisions were done by "duplications" and "mediations", for example 69×19=69×(16+2+1), where 16 represents 4 duplications and 2 a doubling.

Babylonian Sexagesimal Fractions (Cuneiform Documents)

In the quaneiform tablets of the Hammurabi dynasty (1800-1600 BC) appears the positional system, previously referred to, extended to the fractions, but XXX is worth for 2× × 60+2{displaystyle 2times 60+2}, 2+2× × 60− − 1{displaystyle 2+2times 60-1} or 2× × 60− − 1+2× × 60− − 2{displaystyle 2times 60-1+2times 60-2} with a representation based on the interpretation of the problem.

To calculate, as we used before having machines, the numerous tables that were available: To multiply, of reverses, of squares and cubes, of square and cubic roots, of successive powers of a given number not fixed, etc. For example, to calculate a{displaystyle a}They took their best whole approach. a1{displaystyle a_{1}}and calculated b1=a/a1{displaystyle b_{1}=a/a_{1}} (one older and one younger) and then a2=(a1+b1)/2{displaystyle a_{2}=(a_{1}+b_{1})/2} is better approximation, proceeding the same we get b2=a/a2{displaystyle b_{2}=a/a_{2}}} and a3=(a2+b2)/2{displaystyle a_{3}=(a_{2}+b_{2})/2} obtained in the Yale-7289 2=1;24,51,10 (based decimal 1,414222) tablet as value of a3{displaystyle a_{3} starting from a1=1;30{displaystyle a_{1}=1;30} (see Babylonian algorithm).

They performed the operations in a similar way to today, division multiplying by the inverse (for which they use their inverse tables). In the table of inverses, those of 7 and 11 that have an infinitely long sexagesimal expression are missing. Yes, there are 1/59=;1,1,1 (our 1/9=0.111…) and 1/61=;0.59,0.59 (our 1/11=0.0909…), but they did not notice of periodic development.

Discovery of the immeasurables

The circumstances and date of this discovery are uncertain, although it is attributed to the Pythagorean school (the Pythagorean Theorem is used). Aristotle mentions a demonstration of the incommensurability of the diagonal of a square with respect to its side based on the distinction between even and odd. The reconstruction carried out by C. Boyer is:

Sean d:diagonal, s:lado and d/s rational that we can write it as p/q{displaystyle p/q} with p and q cousins. For the theorem of Pythagoras we have to d2=s2+s2{displaystyle d^{2}=s^{2}+s^{2}}}, (d/s)2=p2/q2=2{displaystyle (d/s)^{2}=p^{2}/q^{2}=2}, then p2=2q2{displaystyle p^{2}=2q^{2}} and therefore p2{displaystyle p^{2}} must be pair and also p, and therefore q impar. Being p pair we have p=2r{displaystyle p=2r}, then 4r2=2q2{displaystyle 4r^{2}=2q^{2}} and 2r2=q2{displaystyle 2r^{2}=q^{2}}, then q2{displaystyle q^{2}} it is par and q also, then q is par and odd with what we have a contradiction.

The Pythagorean theory of everything is number was seriously damaged.

The problem would be solved by Eudoxo de Cnido (408-355 a. C.) as indicated by Euclides in book V of The elements. To this end it established the Axiom of Archimedes: Two magnitudes have a reason if you can find a multiple of one of them that exceeds the other (excludes 0). Then in the Definition-5 gives the famous formulation of Eudoxo: Two magnitudes are in the same reason a/b=c/d{displaystyle a/b=c/d} if you give two natural numbers any m and n, yes ma=nb{displaystyle ma=nb} then. mc=nd{displaystyle mc=nd} (definition that exchanging the 2nd and 3rd terms is equivalent to our current procedure).

In the book of J.P. Colette observes that this definition is very close to the real number that Dedekind will give in the centuryXIXdivide the fractions into the m/n{displaystyle m/n} such that ma=nb{displaystyle ma=nb} and those that don't.

Creation of zero

In any positional numbering system arises the problem of the lack of units of certain order. For example, in the Babylonian system the number 32{displaystyle 32} written in base 60 can be 3× × 60+2{displaystyle 3times 60+2} or 3× × 602+0× × 60+2{displaystyle 3times 60^{2}+0times 60+2}. Sometimes the empty position was used to avoid this problem 3 _ 2; but the scribes should be very careful not to be mistaken.

Circa III century B.C. C., in Greece, nothing began to be represented by an "o" which means oudos 'empty', and which did not give rise to the concept of zero as it exists today. The idea of zero as a mathematical concept seems to have arisen in India long before anywhere else. The only old world ordinal notation was Sumerian, where zero was represented by a void.

In America, the first known expression of the pre-Hispanic vigesimal numeral system dates from the III century B.C. C. It is a late Olmec stela, which already had both the concept of "order" as the one of "zero". The Mayans invented four signs for zero; the main ones were: the cut of a snail for the mathematical zero, and a flower for the calendrical zero (which implied not the absence of quantity, but the fulfillment of a cycle).

Negative numbers

Brahmagupta, in AD 628, considers the two roots of quadratic equations, even if one of them is negative or irrational. In fact, it is the first time in his work that the arithmetic (+, -, *, /, powers and roots) of positive and negative numbers and zero appears systematized, which he called goods, debts and nothingness. So, for example, for the quotient, he states:

Positive divided by positive, or negative divided by negative, is yes. Number divided by number is nothing (0/0=0). Positive divided by negative is negative. Negative divided by affirmative is negative. Positive or negative divided by number is a fraction that has it as denominator (a/0=¿?)

He not only used negatives in the calculations, but considered them as isolated entities, without reference to geometry. All this was achieved thanks to his lack of concern for rigor and logical foundation, and his mixture of the practical with the formal.

However, their treatment of the negatives fell into a vacuum, and it took several centuries (until the Renaissance) for it to be recovered.

Apparently, the Chinese also had the idea of negative numbers, and were used to calculating with them using black rods for negatives and red rods for positives.

Transmission of the Indo-Arabic system to the West

Several authors of the centuryXIII They contributed to this diffusion, highlight Alexandre de Villedieu (1225), Sacrobosco (circa 1195, or 1200-1256) and above all Leonardo de Pisa (1180-1250). The latter, known as Fibonacci, traveled through the East and learned from the Arabs the Hindu positional system. He wrote a book, The Liber abaci, which deals in chapter I with positional numbering, in the following four elementary operations, in chapters VI and VII the fractions: common, sexagesimales and unitarian (do not use decimals, main advantage of the system!), and in chapter XIV the square and cubic radicals. It also contains the problem of rabbits giving the series: 1,1,2,3,5,8,...,un{displaystyle 1,1,2,3,5,8,...,u_{n}} with un=un− − 1+un− − 2{displaystyle u_{n}=u_{n-1}+u_{n-2}}.

Negative numbers do not appear, which the Arabs did not consider either, due to the identification of number with magnitude (an obstacle that would last for centuries!). Despite the advantage of their calculation algorithms, a fierce struggle between abacists and algorists would break out for various reasons, until the final triumph of the latter.

Continued Fractions

Pietro Antonio Cataldi (1548-1626), although with numerical examples, develops a square root in continuous fractions like today: We want to calculate N{displaystyle N} and be a{displaystyle a} the greater number whose square is less than N{displaystyle N} and b=N2− − a2{displaystyle b=N^{2}-a^{2}}We have: N− − a=(N2− − a2)/(N+a)=b/(2a+N− − a)=b/(2a+(b/2a+...)){displaystyle N-a=(N^{2}-a^{2})/(N+a)=b/(2a+N-a)=b/(2a+(b/2a+...))} that with his notation he wrote: n=a fanb/2.a. strangerb/2.a... Thus 18=4 fake2/8. stranger2/8, which gives approximations 4+(1/4), 4+(8/33)...

This being the irrational numbers accepted with all normality, since they could be easily approximated by rational numbers.

First formulation of complex numbers

The complex numbers were in few cases accepted as roots or solutions of equations (M. Stifel (1487-1567), S. Stevin (1548-1620)) and by almost none as coefficients). These numbers were initially called ficticii 'fictitious' (The term 'imaginary' currently used is reminiscent of this reluctance to consider them respectable numbers.) Despite this, G. Cardano (1501-1576) knows the rule of signs and R. Bombelli (1526-1573) knows the additive rules through haberes and debits, but they are considered formal manipulations to solve equations, without entity as they do not come from measurement or counting.

Cardano in the resolution of the problem divide 10 into two parts such that your product is worth 40 obtains as solutions 5+− − 15{displaystyle 5+{sqrt {-15}}} (in its notation 5p:Rm:15) and 5− − − − 15{displaystyle 5-{sqrt {-15}}} (in notation 5m:Rm:15), solutions that considered mere manipulations "sutiles, but useless".

In the resolution of cubic equations with the formula of Cardano-Tartaglia, although the roots are real, they appear in the intermediate steps roots of negative numbers. In this situation Bombelli says in his Algebra He had what he called "a crazy idea", this was that the radicals could have the same relationship as those living and operating with them, trying to eliminate them later. In a later text in 20 years he uses p.d.m. (+i){displaystyle (+mathrm {i}}}} for +− − 1{displaystyle +{sqrt {-1}}} and m.d.m. (− − i){displaystyle (-mathrm {i}}}} for − − − − 1{displaystyle}{sqrt {-1}}} giving the rules to operate with these symbols adding that whenever one of these expressions appears it also appears its conjugate, as in the equations of 2.o degree that solves correctly. Gives a method to calculate a+bi{displaystyle a+bmathrm {i} }.

Generalization of Decimal Fractions

Although there is a more than casual use of decimal fractions in medieval Arabia and Renaissance Europe, and as early as 1579 Vieta (1540-1603) proclaimed his support for them over sexagesimals, and they were accepted by mathematicians that were dedicated to research, its use became widespread with the work that Simon Stevin published in 1585 De Thiende (La Disme). In his first definition, he says that Disme is a kind of arithmetic that allows all accounts and measurements to be made using only natural numbers. In the following, it defines our integer part: any number that goes first is called beginning and its sign is (0), (first decimal position 1/10). The next one is said first and its sign is (1) (second decimal position 1/100). The next one is called second (2). That is, the decimal numbers you write: 0.375 as 3(1)7(2)5(3), or 372.43 as 372(0)4(1)3(2). He adds that no broken numbers (fractions) are used, and the number of signs, except 0, never exceeds 9 .

This notation was simplified by Joost Bürgi (1552-1632) by removing the mention of the order of the figures and replacing it with a «.» at the top of the units 372·43, shortly after Magini (1555-1617) used the «.» between the units and the tenths: 372.43, a use that would be generalized when it appeared in the Constructio of Napier (1550-1617) of 1619. The «,» was also used at the beginning of the century XVII by Dutchman Willebrord Snellius: 372.43.

The principle of mathematical induction

Its background is a demonstration method, called complete induction, by repeated application of the same siloge that extends indefinitely and used Maurolyco (1494-1575) to demonstrate that the sum of the first n{displaystyle n} odd natural numbers is the square of n{displaystyle n}- That's a term. 1+3+5+7+ +(2n− − 1)=n2{displaystyle 1+3+5+7+dots +(2n-1)=n^{2}}}. Pascal (1623-1662) used the mathematical induction method, in its abstract formulation, as we know it today, to test properties related to the numerical triangle bearing its name. The induction demonstration always consists of two parts: the base step and the inductive step, which are described below in modern notation:

Yeah. S{displaystyle S} is a subset of natural numbers (denoted by N{displaystyle mathbb {N} }) where each element n{displaystyle n} fulfills the property P(n){displaystyle P(n)} and you have to:

1. 0{displaystyle} belongs to S{displaystyle S}.
2. The fact that n{displaystyle n} be a member of S{displaystyle S} implies that n+1{displaystyle n+1} It is too.

then. S=N{displaystyle S=mathbb {N} }, i.e. all natural numbers n{displaystyle n} have the property P(n){displaystyle P(n)}.

Intuitively, induction is understood as a domino effect. Assuming you have an infinite row of dominoes, the base step is equivalent to throwing the first domino; on the other hand, the inductive step is equivalent to proving that if any tile falls, then the next tile will also fall. The bottom line is that all the tiles in that row can be dropped.

The geometric interpretation of complex numbers

This interpretation is usually attributed to Gauss (1777-1855) who made his doctoral thesis on the fundamental theorem of algebra, first enunciated by Harriot and Girard in 1631, with demonstration attempts made by D’Alembert, Euler and Lagrange, demonstrating that the previous tests were false and giving a correct demonstration first for the case of coefficients, and after complexes. He also worked with complex integers adopting the form a+bi{displaystyle a+bi}, with a{displaystyle a} and b{displaystyle b} Whole. This symbol i{displaystyle i} for − − 1{displaystyle {sqrt {1}} was first introduced by Euler in 1777 and disseminated by Gauss in his work Disquisitions arithmeticae 1801.

The graphical representation of complex numbers had already been discovered by Caspar Wessel (1745-1818) but it went unnoticed, and thus the plane of complex numbers is called «Gauss plane» despite not to publish his ideas until 30 years later.

Since Girard's time (mid-XVII century) it was known that real numbers can be represented in correspondence with points of a line. By now identifying the complexes with the points in the plane, mathematicians will feel comfortable with these numbers, seeing is believing.

Discovery of transcendental numbers

The distinction between algebraic and transcendent irrational numbers dates back to the centuryXVIIIat the time Euler showed that e{displaystyle e} and e2{displaystyle e^{2}} are irrational and Lambert that is π. Legendre's works on the hypothesis that π could not be the root of an algebraic equation with rational coefficients, pointed out the way to distinguish different types of irrational. Euler already made this distinction in 1744, but almost a century would have to be expected to clearly establish the existence of the transcendent irrationals in the works of Liouville, Hermite and Lindeman.

Liouville (1809-1882) showed in 1844 that all numbers of the form a1/10+a2/102!+a3/103!+...{displaystyle a_{1}/10+a_{2}/10^{2} +a_{3/10}^{3}+... ! (e.g., 0,101001) are transcendent.

Hermite (1822-1901) in memory On the exponential function of 1873 demonstrated the importance of e{displaystyle e} testing in a very sophisticated way that the equation: c0+c1e+...+cnen=0{displaystyle c_{0}+c_{1}e+c_{n}e^{n=} It can't exist.

Lindeman (1852-1939) in memory About the number e{displaystyle e} 1882 proves that the number and cannot satisfy the equation: c1ex+c2ex+............+cnex=0{displaystyle c_{1}e^{x}+c_{2}e^{x}+.........+c_{n}e^{x}=0} with x{displaystyle x} and ci{displaystyle c_{i}} algebraic, therefore the equation eix+1=0{displaystyle e^{ix}+1=0} has no solution for x algebraic, but doing x=π π {displaystyle x=pi } We've got eπ π i+1=0{displaystyle e^{pi i}+1=0}, then x=π π i{displaystyle x=pi i} cannot be algebraic and as i is then π is transcendent.

Hilbert's 7th Problem (1862-1943) ab{displaystyle a^{b}, with algebraic other than zero and one, and b irrational algebraic, it is transcendent was resolved affirmatively by Gelfond (1906-1968) in 1934. But it is not known whether they are transcendent or not: ee{displaystyle e^{e},eee{displaystyle e^{e^{e}}}, eeee{displaystyle e^{e^{e^{e}}}},... However, e and 1/e are transcendent.

Theories of irrationals

Until the middle of the 19th century mathematicians were content with an intuitive understanding of numbers and their simple properties were not established logically until the XIX century. The introduction of rigor in the analysis revealed the lack of clarity and imprecision of the system of real numbers, and required its logical structuring on arithmetic bases.

Bolzano had made an attempt to construct the real numbers based on sequences of rational numbers, but his theory went unnoticed and was not published until 1962. Hamilton made an attempt, referring to the magnitude of time, from partitions of numbers rational:

Yeah. a=n1m1{displaystyle a={cfrac {n_{1}}{m_{1}}}}},

When b=n12m12{displaystyle b={cfrac {n_{1}{2}}{m_{1}{2}}}}{1⁄2}}}}}}

And yes. a=n2m2{displaystyle a={cfrac {n_{2}}{m_{2}}}}}

When b=n22m22Δ Δ a=b{displaystyle b={cfrac {n_{2}{2}}{m_{2}{2}}}}}{quad longrightarrow quad a={sqrt {b}}}}}}}}

But he didn't develop his theory anymore.

But in the same year, 1872, five mathematicians, one French and four German, published their works on the arithmetization of real numbers:

• Charles Meray (1835-1911) in his work Nouveau précis d’analyse infinitesimale defines the irrational number as a limit of successions of rational numbers, without bearing in mind that the very existence of the limit presupposes a definition of the actual number.

• Hermann Heine (1821-1881) published in the Journal of Crelle In 1872, his article “The Elements of the Theory of Functions”, where he proposed ideas similar to those of Cantor, a theory which is now called “Heine-Cantor Theorem”.

• Richard Dedekind (1831-1916) publishes his Stetigkeit und irrationale zahlen. His idea is based on the continuity of the real line and the "holes"that there are if we only consider the rational numbers. In the section dedicated to "domain R» enunciates an axiom by which the continuity of the line is established: «each point of the straight divides the points of this into two classes such that each point of the first is to the left of each point of the second class, then there is a single point that produces this division». This same idea uses it in the section "creation of irrational numbers» to introduce your concept of «cut». Bertrand Russell would aim after it's enough with one class, because it defines the other.

• Georg Cantor (1845-1918). It defines the concepts of: fundamental succession, elemental succession, and limit of a fundamental succession, and from them defines the actual number.

• Karl Weierstrasss (1815-1897). He did not publish his work, continuation of those of Bolzano, Abel and Cauchy, but was known for his teachings at the University of Berlin. Its characterization based on the «intervals embedded», which can be contracted to a rational number but not necessarily do, is not as generalizable as the previous ones, but provides easy access to decimal representation of the real numbers.

Hypercomplex Algebras

The construction of obtaining the complex numbers from the real numbers, and its connection with the group of affine transformations in the plane suggested other similar generalizations known as hypercomplex numbers to some mathematicians. In all these generalizations the complex numbers are a subset of these new number systems, although these generalizations have the mathematical structure of algebra over a field, but in them the multiplication operation is not commutative.

Set Theory

Set theory suggested many different ways to extend the natural numbers and the real numbers in ways different from how the complex numbers extended the set of real numbers. The attempt to capture the idea of a set with a non-finite number of elements led to the arithmetic of transfinite numbers that generalize to natural numbers, but not to integers. Transfinite numbers were introduced by Georg Cantor around 1873.

The hyperreal numbers used in non-standard analysis generalize to reals but not to complex numbers (although they admit a complexification that would generalize to complex numbers as well). Although it seems that the hyperreal numbers do not provide interesting mathematical results that go beyond those obtainable in actual analysis, some mathematical proofs and demonstrations seem simpler in the formalism of the hyperreal numbers, so they are not without practical importance.

Socially

• Natural numbers due to the need to count.
• Fractionary numbers due to the need to measure parts of a whole, and share.
• Negative integers for dual sense phenomena: left-right, top-down, loss-winning.
• Real numbers for the need to measure segments.
• Complex numbers due to the requirements of solving algebraic equations, such as cubic or x² + 1 = 0.

Number representation systems

Cipher, digit and numeral

One of the most frequent ways of representing numbers in writing consists of a "finite set of symbols" or digits that, properly combined, make it possible to form numbers that function as representations of numbers (when a specific sequence of signs is used to represent a number is called a numeral, although a figure can also simply represent an identification code).

Number base

Both natural languages and most numeral systems use a finite inventory of units to express a much larger number of numbers. An important way to achieve this is the use of base arithmetic in those systems a number is generally expressed by addition or multiplication of numbers. Purely arithmetic systems use bases where each sign receives a different interpretation depending on its position. Thus in the following Arabic numeral (base 10):

13568{displaystyle 13568,}

The <8> because it is in the last position it represents units, the <6> represents tens, the <5> hundreds, the <3> thousands and the <1> tens of thousands. That is, that numeral will represent the number:

n 13568 =1⋅ ⋅ 104+3⋅ ⋅ 103+5⋅ ⋅ 102+6⋅ ⋅ 101+8⋅ ⋅ 100=13568{displaystyle n_{langle 13568rangle }=1cdot 10^{4+3cdot 10^{3}+5cdot 10^{2}+6cdot 10^{1}+8cdot 10^{0}=13568}

Many languages in the world use a decimal basis, just like the arabic system, although it is also common for languages to use vigesimal systems (base 20). In fact the idea of using a finite number of digits or signs to represent arbitrary large numbers works for any base bwhere b is an integer greater or equal to 2. Computers often use the binary base for their operations (b = 2), and for certain uses the octal base is also used (b = 8) or hexadecimal (b = 16). The base matches the number of primary signs, if a positional system has b primary symbols that we will designate for {0,1,2...... ,b− − 1!{displaystyle {0,1,2dotsb-1}}the numeral:

SnSn− − 1...... S2S1S0Si한 한 {0,1,2...... ,b− − 1!{displaystyle S_{n}S_{n-1}dots S_{2}S_{1}S_{0}S_{0}qquad S_{i}in {0,1,2dotsb-1}}

It will designate the number:

n SnSn− − 1...... S2S1S0 =Sn⋅ ⋅ bn+ +S2⋅ ⋅ b2+S1⋅ ⋅ b1+S0⋅ ⋅ b0=␡ ␡ k=0nSkbk{displaystyle n_{langle S_{n}S_{n-1}dots S_{2}S_{1}S_{0}rangle }=S_{n}{n}{ncdot b^n}{n}{nx1⁄2}{2}{2}{2}{2}

Numbers in natural languages

Natural languages use names or numerals for numbers often based on finger counting, which is why most languages use base 10 (fingers) or base 20 (fingers) numeral systems. and feet), although there are also some exotic systems that use other bases.