NP hard
In computational complexity theory, the complexity class NP-hard (or NP-complex, or NP-hard) is the set of decision problems that contains problems H such that every problem L in NP can be polynomially transformed into H. This class can be described as the one that contains decision problems that are at least as difficult as an NP problem. This statement is justified because if we can find an algorithm A that solves one of the NP-hard H problems in polynomial time, then it is possible to build an algorithm that works in polynomial time. polynomial for any NP problem by first executing the reduction of this problem in H and then executing the A algorithm.
Assuming the language L is NP-complete,
- 1. L It's in. NP
- 2. Русский NP, L' ≤ L
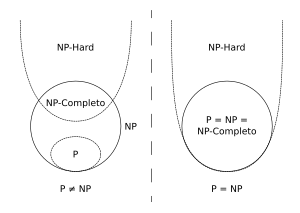
In the NP-Hard set it is assumed that the language L satisfies property 2, but not property 1.
The class NP-complete can alternatively be defined as the intersection between NP and NP-hard.
Some consequences of the definition are:
- As NP-complete is the most expensive type of NP class, the problem H is at least as expensive as NP, but H it doesn't have to be in NP and therefore it doesn't have to be a decision problem.
- NP-complete problems can be transformed into one another by a polynomial reduction, NP-complete problems can be solved in polynomic time by reduction to H, so all NP problems are reduced to H; however, this involves using two different types of transformations: from NP-complete decision problems to a NP-complete problem L and polynomial transformations L a H by polynomial reduction of Turing.
- If there is any polynomic algorithm to solve an NP-hard problem, then there are algorithms to solve all NP problems in polynomic time, this would mean that P=NP.
- If an optimization problem H has an NP-complete version, then H It's NP-hard.
- Yeah. H belongs to NP, then H It also belongs to NP-complete because in this case there is a polynomial transformation of Turing that meets the requirements of polynomial transformations.
A common mistake is to think that NP in NP-hard means non-polynomial, since although there are serious suspicions that there are no algorithms to solve these problems in polynomial time, this has never been proven.
Examples
The subset addition problem is an example of an NP-hard problem and is defined as follows: given a set S of integers, does there exist a non-empty subset of S whose elements sum to zero?
There are NP-hard problems that are not NP-complete, for example the stopping problem. This problem involves taking a program and its data and deciding whether to terminate or run forever. This is a decision problem and it is easy to show that it is NP-hard but not NP-complete. For example, the Boolean satisfiability problem can be reduced to the halting problem by transforming it into a description of a Turing machine that tests all variable values; when it finds a combination that satisfies the formula, it stops and otherwise retries from the beginning, staying in an infinite loop. To see that the stopping problem is not in NP, it is enough to note that all NP problems have an associated algorithm but the stopping problem is undecidable.
Naming convention including the initials NP
Problem family names with the acronym NP is somewhat confusing. The NP-hard problems are not all NP, despite the fact that these acronyms appear in the family name. However, the names are currently very entrenched and suggesting a change of nomenclature is unrealistic. On the other hand, the families of problems with the initials NP are all defined taking the NP family as a reference:
- NP-complete — means problems that are complete in NP, that is, the most difficult to resolve in NP;
- NP-hard - (NP-difficulty) means at least as complex as NP (but not necessarily in NP);
- NP-easy - (NP-easy) means a lot. as difficult as NP (but not necessarily in NP);
- NP-equivalent — it means equally difficult for NP, but not necessarily in NP.
Contenido relacionado
Nicolas Bourbaki
Diameter
Asymptote