Newton's laws

ImprimirCitar

Newton's first and second law, in Latin, in the original edition of his work Mathematica Principia

Newton's laws, also known as Newton's laws of motion, are three principles that explain a large part of the problems raised in classical mechanics, particularly those related to the movement of bodies, which revolutionized the basic concepts of physics and the movement of bodies in the universe.

They constitute the foundations not only of classical dynamics but also of classical physics in general. Although they include certain definitions and in a sense can be seen as axioms, Newton said they were based on quantitative observations and experiments; they can certainly not be derived from other more basic relationships. The proof of its validity lies in its predictions... The validity of these predictions was verified in every case for more than two centuries.

Specifically, the relevance of these laws lies in two aspects: on the one hand, they constitute, together with the Galileo transformation, the bases of classical mechanics, and on the other, by combining these laws with the law of universal gravitation, Kepler's laws of planetary motion can be deduced and explained. Thus, Newton's laws make it possible to explain, for example, both the movement of the stars and the movements of artificial projectiles created by humans and all the mechanics of machine operation. The mathematical formulation of it was published by Isaac Newton in 1687 in his work Philosophiæ naturalis principia mathematica .

Newton's dynamics, also known as classical dynamics, only holds in inertial reference frames (moving at constant velocity; the Earth, though it twists and turns, is treated as such for the purposes of many practical experiments). It is only applicable to bodies whose speed is considerably far from the speed of light; When the speed of the body approaches 300,000 km/s (which would occur in non-inertial reference systems), a series of phenomena called relativistic effects appear. The study of these effects (length contraction, for example) corresponds to the theory of special relativity, enunciated by Albert Einstein in 1905.

Theoretical foundations

Portrait of Sir Isaac Newton (1642-1727)

The first concept that Newton handles is that of mass, which he identifies with «amount of matter». Newton then assumes that the amount of movement is the result of the product of the mass times the velocity. Third, he points out the importance of distinguishing between the absolute and the relative whenever one speaks of time, space, place, or movement.

In this sense, Newton, who understands movement as a translation of a body from one place to another, to arrive at the absolute and true movement of a body:

[...] composes the movement (relative) of that body in the place (relative) in which it is considered, with the movement (relative) of the place itself in another place where it is located, and so on, step by step, until reaching a place immobileI mean, the system of references of absolute movements.

In accordance with this approach, it establishes that the apparent movements are the differences of the true movements and that the forces are their causes and effects. Consequently, the force in Newton has an absolute character, not a relative one.

The laws enunciated by Newton, and considered the most important of classical mechanics, are three: the law of inertia, the relationship between force and acceleration, and the law of action and reaction. Newton stated that all movements follow these three main laws, formulated in mathematical terms. One concept is force, the cause of movement, and another is mass, the measurement of the amount of matter set in motion; the two are usually referred to by the letters F and m.

Newton's first law or law of inertia

The first law of motion refutes the Aristotelian idea that a body can only be kept in motion if a force is applied to it. Newton states that:

Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.
Every body continues in its state of rest or movement uniform in a straight line, not far from the printed forces to change its position.

This law postulates, therefore, that a body cannot change its initial state by itself, either at rest or in uniform rectilinear motion, unless a force or a series of forces is applied whose resultant is not zero. Newton takes into account, thus, the fact that bodies in motion are constantly subjected to forces of friction or friction, which slows them down progressively, something new with respect to previous conceptions that understood that the movement or detention of a body was due exclusively to to whether a force was exerted on them, but never understanding friction as such.

Consequently, a body that moves with uniform rectilinear motion implies that there is no net external force or, in other words, a moving object does not stop naturally if a force is not applied to it. In the case of bodies at rest, it is understood that their speed is zero, so if it changes it is because a net force has been exerted on that body.

Newton returned to Galileo's law of inertia: the tendency of a moving object to continue moving in a straight line, unless influenced by something to throw it off its path. Newton assumed that if the Moon did not shoot out in a straight line, along a line tangential to its orbit, it was due to the presence of another force pushing it toward the Earth, constantly diverting its path into a circle. Newton called this force gravity and believed that it acted at a distance. There is nothing physically connecting the Earth and the Moon and yet the Earth is constantly pulling the Moon towards us. Newton used Kepler's third law and mathematically deduced the nature of the force of gravity. He showed that the same force that made an apple fall to Earth kept the Moon in its orbit.

Newton's first law establishes the equivalence between the state of rest and uniform rectilinear motion. Let us suppose a reference system S and another S´ that moves with respect to the first one at a constant speed. If a net force does not act on a particle at rest in the system S´, its state of motion will not change and it will remain at rest with respect to the system S´ and with rectilinear motion uniform with respect to the S system. Newton's first law is satisfied in both reference frames. These frames in which Newton's laws are satisfied are called inertial reference frames. No inertial reference system has preference over another inertial system, they are equivalent: this concept constitutes the Galileo or Newtonian principle of relativity.

The fundamental statement that we can extract from Newton's law is that

{displaystyle sum mathbf {F} =mathbf {0} ;Leftrightarrow ;{frac {mathrm {d} mathbf {v} }{mathrm {d} t}}=mathbf {0}.}

This expression is a vector equation, since the forces have direction and sense. On the other hand, it should be noted that the variation of the speed corresponds to the acceleration.

Inertial reference frames

Main article: Inertial reference system

Newton's first law serves to define a special type of reference frames known as inertial reference frames, which are those from which it is observed that a body on which no net force acts moves with constant velocity.

A reference frame with acceleration (and the normal acceleration of a rotating frame is included in this definition) is not an inertial frame, and observation of a particle at rest in the frame itself will not satisfy Newton's laws (since that acceleration will be observed without the presence of any net force). They are called non-inertial reference frames.

Variance of an approach to a problem due to the possibility of observing it from two points of view: the point of view of an external observer (inerial) or from an internal observer

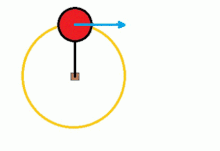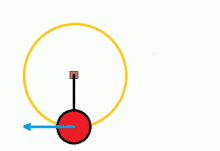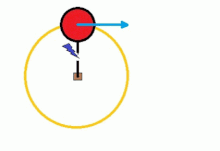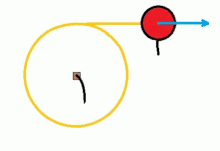
For example, consider a platform rotating with a constant angular velocity, ω, in which an object is tied to the axis of rotation by a rope, and suppose two observers, one inertial external to the platform and another non-inertial located on it.

Inertial observer: from his point of view the block moves in circle with speed v and is accelerated to the center of the platform with a centripetal acceleration ${displaystyle a={tfrac {v^{2}}{r}}}$ . This acceleration is the consequence of the force exercised by the tension of the rope.
Non-inertial observer: for the observer who rotates with the platform the object is at rest, a = 0. That is, it observes a fictitious force that counters the tension so that there is no centripetal acceleration. That force must be ${displaystyle F_{c}={tfrac {mv^{2}}{r}}}$ . This observer feels the strength as if it were perfectly real, even if it is only the consequence of the acceleration of the reference system in which it is located.

In reality, it is impossible to find an inertial reference frame, since there are always some kind of forces acting on the bodies; however, it is always possible to find a frame of reference in which the problem we are studying can be treated as if we were in an inertial frame. In many cases, the Earth is a good approximation of an inertial system, since despite having a translational and a rotational acceleration, both are of the order of 0.01 m/s² and, consequently, we can consider that a reference system of an observer on the earth's surface is an inertial reference frame.

Applications of Newton's First Law

A ball tied to a string can be considered as an illustrative example of this first law or law of inertia, so that the ball rotates following a circular path. Due to the centripetal force of the string (tension), the mass follows a circular path, but if the string were to break at some point, the ball would take a straight line in the direction of the ball's velocity at the instant of breakage..

After breaking, the net force exerted on the ball is 0, so it will experience, as a result of a state of rest, a uniform rectilinear motion.

Newton's second law or fundamental law of dynamics

Originally, Newton's second law states that:

Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa printitur.
The change of movement is directly proportional to the printed motor force and occurs according to the straight line along which the force is printed.

It is important to note that Newton did not have a single notion of force: these could be inertial forces (vis insita), impressed forces (vis impressa) or centripetal forces (vis centripeta). Specifically, according to the second law, any impressed force is the cause of an observable variation in the motion of an object. The second law that Newton originally proposed does not make an explicit mention of mass, acceleration or the variation of velocity in time, however the change in motion is considered as a way of describing the variation in "momentum"., which in its current form is a vector quantity. In modern terms, the motion of an object is described by its momentum (or moment):

${displaystyle mathbf {p} =mmathbf {v} }$ ,

where $m$ is the mass of the object and ${mathbf {v}}$ his speed. (This is the approximate form found in classical mechanics.) Thus, Newton's second law (or fundamental law of dynamics) can be applied mathematically as

${displaystyle mathbf {F} ={frac {dmathbf {p} }{dt}}}$

That is, the force that generates the movement is directly proportional to the change in momentum in each unit of time. From this equation, the unit of measure of force in the International System of Units, the Newton, is obtained:

${displaystyle 1,{text{N}}=1,{frac {{text{kg}}cdot {text{m}}}{{text{s}}^{2}}}}$

Newton's second law is only valid in inertial reference frames but even if the reference frame is non-inertial, the same equation can be used including the fictitious forces (or inertial forces).

Representation of the sum of forces. Here you are adding twice the force No. 2. The resulting (marked with red) responds to the following equation:

{displaystyle {overrightarrow {F}}_{rm {resultante}}={overrightarrow {F_{1}}}+2cdot {overrightarrow {F_{2}}}+{overrightarrow {F_{3}}}}

It should be noted that when multiple forces act on an object, Newton's second law refers to the net force acting on it. So the change in the momentum of an object is given by the vector sum of all the forces acting in it. This is known as the principle of superposition of forces: if $K$ forces act on the same object, then the net force is given by

${displaystyle mathbf {F} =sum _{i=1}^{K}mathbf {F} _{i}}$

In geometric terms, it is also known as the parallelogram rule. This principle appears included in Newton's Principia as Corollary 1, after the third law, but it is an essential requirement for the understanding and application of the laws, as well as for the vector characterization of forces.

Special cases

Introducing the definition of momentum, as mass times velocity, in Newton's second law, two important cases can be recognized: when the mass of the object is constant and when it varies.

Constant Mass

If the mass of the body remains constant, then Newton's second law implies that

${displaystyle mathbf {F} =m{frac {dmathbf {v} }{dt}}=mmathbf {a} }$

That is, the acceleration acquired by an object is proportional to the net force applied to it, the constant of proportionality being the inertial mass of the object. Since force and acceleration are vectors, the second law implies that these vectors are parallel.

Variable mass

When the mass of the object varies, then Newton's second law takes the form

${displaystyle mathbf {F} =m{frac {dmathbf {v} }{dt}}-mathbf {v} _{rel}{frac {dm}{dt}}}$

where ${mathbf {F}}$ is the net force on the object, ${displaystyle mathbf {v} _{rel}}$ is the relative speed of the mass that is entering or escaping with respect to the mass center of the object, and ${mathbf {v}}$ is the speed of the main object.

Impulse

The fundamental law of dynamics establishes that a variation in momentum can be expressed as a function of the force acting on it and the time interval during which the force is exerted:

${displaystyle Delta mathbf {p} =mathbf {F} Delta t}$

In the limit in which the time interval tends to 0, we have the differential form

${displaystyle dmathbf {p} =mathbf {F} dt}$

If the force is variable in time, this equation can be integrated between a given interval, say between ${displaystyle t_{1}}$ and ${displaystyle t_{2}}$ , being like

${displaystyle mathbf {I} =int _{t_{1}}^{t_{2}}mathbf {F} dt=int _{mathbf {p} _{1}}^{mathbf {p} _{2}}dmathbf {p} =mathbf {p} _{2}-mathbf {p} _{1}=Delta mathbf {p} }$

The vector quantity ${mathbf {I}}$ is called linear impulse and represents a physical magnitude that is also manifested in quick actions or impacts, such as shocks, carrying direction and sense module. Its units in the International System are ${displaystyle {text{kg}}cdot {frac {text{m}}{text{s}}}}$ . In this type of action it is appropriate to consider the duration of the impact and the force exercised during it.

Applications of Newton's second law

Among the possible applications of Newton's Second Law, we can highlight:

Free fall

Free Fall: It is a movement that is observed when an object falls from a certain height on the surface of the Earth, in which the only force on the object considered is its own weight. To study the movement you can choose a coordinate system where the origin of the axis and is on the latter and is positive in the direction contrary to the force of gravity at that point ("up"). In this system both the speed of fall and the acceleration of gravity have a negative sign. In the example represented, the object is supposed to fall from the rest, but it may fall from an initial rate other than zero.

Simple Module: Force Diagram

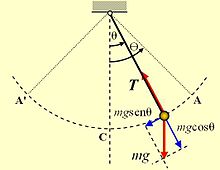
Simple Pendulum: M-Particle suspended from point O by an inextensible thread of length l and despicable mass. If the particle moves to a θ position₀ (angle that makes the thread with the vertical) and then looses, the pendulum starts to swing. The pendulum describes a circular trajectory, an arch of a radio circle l. The forces acting on the mass particle m are two, weight and tension T the thread.

If the second law is applied, in the radial direction:

${displaystyle mcdot a_{n}=T-mgcdot cos {theta }}$

where a_n represents the acceleration normal to the trajectory. Knowing the value of the speed v in the angular position, the tension T of the thread can be determined. It is maximum when the pendulum passes through the equilibrium position.

${displaystyle T=mg+{{mcdot v^{2}} over {ell }}}$ ,

where the second term represents the centrifugal force.

And the tension is minimal, at the ends of its trajectory, when the velocity is zero

${displaystyle T=mgcdot cos {theta }}$

in the tangential direction:

${displaystyle mcdot a_{t}=-mgcdot operatorname {sen} {theta }}$

where a_t represents the acceleration tangent to the trajectory.

Newton's third law or principle of action and reaction

Newton's third law states that whenever one object exerts a force on a second object, the second object exerts a force of equal magnitude and direction, but in the opposite direction, on the first. It is often stated like this: every action is always opposed by an equal reaction, but in the opposite direction. In any interaction there is a pair of action and reaction forces located in the same direction with equal magnitude and opposite directions. Newton's original formulation is:

Actioni contram semper " æqualem esse reactionem: sive corporum duorum actiones in se mutual semper esse æquales " in opposite parts direct.
Every action always occurs an equal and contrary reaction: it means that the mutual actions of two bodies are always equal and directed in the opposite sense.

This third law of Newton is completely original (since the first two had already been proposed in another way by Galileo, Hooke and Huygens) and makes the laws of mechanics a logical and complete set. It states that for each force acting on a body, it exerts a force of equal intensity, but in the opposite direction, on the body that produced it. In other words, the forces, located on the same line, always appear in pairs of equal magnitude and direction, but with opposite directions. If two objects interact, the force F₁₂, exerted by object 1 on object 2, is equal in magnitude with the same direction, but opposite directions to the force F₂₁ exerted by object 2 on object 1:

{displaystyle mathbf {F} _{12}=-mathbf {F} _{21}}

This principle presupposes that the interaction between two particles propagates instantaneously in space (which would require infinite speed), and in its original formulation it is not valid for electromagnetic forces since these do not propagate through space instantaneously but which do so at a finite velocity «c». This principle relates two forces that are not applied to the same body, producing different accelerations in them, depending on their masses. Otherwise, each of these forces separately obeys the second law. Together with the previous laws, this allows us to state the principles of conservation of linear momentum and angular momentum.

The reaction force (green arrow) increases as the force applied to the object increases (red arrow)

Applications of Newton's Third Law

Some examples where action-reaction forces act are the following:

If an ice skater pushes another of similar weight, the two move at the same speed but in the opposite direction.
By keeping a person standing on Earth, he is pushing the Earth down, not moving because of his great mass, and the Earth makes a push to the person with the same intensity up.
As you walk you push the Earth back with your feet, and the Earth responds by pushing the walker forward, making this advance.
The reaction force that a surface exerts on an object supported by it, called normal force with direction perpendicular to the surface.

Distance forces are not an exception, such as the force that the Earth exerts on the Moon and vice versa, its corresponding pair of action and reaction:

The force that the Earth exerts on the Moon is exactly equal (and of opposite sign) to that exerted by the Moon on the Earth and its value is determined by the law of universal gravitation enunciated by Newton, which establishes that the force that one object exerts on another is directly proportional to the product of their masses, and inversely proportional to the square of the distance that separates them. The force that the Earth exerts on the Moon is responsible for it not leaving its elliptical orbit.

In addition, the force that the Moon exerts on the Earth is also responsible for the tides, which consists of the elevation of the sea water level in some places; for this reason this force is also called tidal force. The tidal force from the Moon is compounded with the tidal force from the Sun providing the complete tidal phenomenon.

Conservation of the amount of movement

The interaction between two or more objects that occurs in a short period of time is called collision or collision.

Balls representing elastic shock

During a collision there are exchanges of energy and momentum between the interacting bodies. In general, according to Newton's first law, in an isolated system of interacting particles, the momentum of the system is conserved; however, the same may not happen with kinetic energy.

Depending on what happens to the kinetic energy during the collision, it can be classified as:

Elastic shock: when the amount of movement and the kinetic energy of the system remain constant. If the sum of the amount of movement of each of the particles is calculated before the shock, the result will be the same as if the sum is made after the particles have crashed. The same is valid for kinetic energy.

Cars representing inelastic shock

Inelastic shock: when the amount of movement remains constant and the kinetic energy varies. As a result, collision bodies may suffer deformations and increase their temperature. After a totally inelastic shock, both bodies have the same speed. The sum of its kinetic energies is less than the initial one because part of it has become internal energy; in most cases it becomes dissipated in the form of heat due to the warming produced in the shock. In the ideal case of a perfectly inelastic clash between macroscopic objects, these remain united with each other after the collision.

History

Aristotle Bust

Lucrecio's bust.

Dynamics is the part of physics that studies the relationships between the movements of bodies and the causes that cause them, specifically the forces that act on them. Dynamics, from the point of view of classical mechanics, is appropriate for the dynamic study of systems that are large in comparison to atoms and that move at speeds much slower than light. To understand these phenomena, the point of starting point is the observation of the everyday world. If you want to change the position of a body at rest, you need to push or lift it, that is, exert an action on it.

Apart from these basic intuitions, the problem of movement is very complex: all those that are observed in nature (falling of an object in the air, movement of a bicycle, a car or a space rocket) are complicated. This motivated that the knowledge about these facts was erroneous for centuries. Aristotle thought that the movement of a body stops when the force that pushes it stops acting. Later it was discovered that this was not true, but Aristotle's prestige as a philosopher and scientist made these ideas endure for centuries, until scientists like Galileo Galilei or Isaac Newton made very important advances with their new formulations. However, there were several physicists who came very close to Newton's formulations long before he formulated his laws of motion. Already in antiquity, Aristotle's physical observations were called into question by peripatetic philosophers such as Strato and Epicurean philosophers such as Lucretius, who declared that "through an undisturbed vacuum, all bodies must travel at the same velocity even when propelled." by unequal weights".

Soto Sunday Bus in Segovia

This is the case of the Spanish Juan de Celaya, a mathematician, physicist, cosmologist, theologian and philosopher who in 1517 published a treatise entitled In octo libros physicorum Aristotelis cum quaestionibus eiusdem, secundum triplicem viam beati Thomae, realium et nominatium , a work of special interest for the study of the origins of the modern science of movement. During his time in France he was a prolific writer, writing mostly about Aristotle's physics and motion. He also published numerous works on philosophy and logic. He was one of the promoters of nominalist logic and the Calculators' Mertonian ideas about dynamics. He was able to state, within Newton's laws, the first law of dynamics (one of the most important laws of physics) a century before Newton.

Another prominent pioneer was Domingo de Soto, also a Spaniard and a disciple of Celaya, a Dominican friar and theologian considered the promoter of modern physics. His theory of uniformly accelerated motion and the fall of basses was the precedent of Newton's law of gravity. He wrote numerous works on theology, law, philosophy and logic and also commented on several books on Aristotelian physics and logic, the most important of which was Quaestiones super octo libros physicorum Aristotelis (1551), on kinematics and dynamics., which was published in various Italian cities, influencing characters such as Benedetti or Galileo. Domingo de Soto was one of the first to establish that a body in free fall undergoes a uniform acceleration with respect to time —this affirmation had also been established by Nicolás Oresme almost two centuries earlier— and his conception of mass was advanced in his time.. In his book Quaestiones he explains the constant acceleration of a freely falling body in this way:

This kind of movement itself happens in the naturally-moved grave and in the projectiles. Where a weight falls from above by a uniform medium, it moves faster in the end than in the beginning. However, the movement of the projectiles is slower at the end than at the beginning: the first one increases evenly disformed, and the second instead decreases evenly disformed.

Domingo de Soto already related two aspects of physics: uniformly warp motion (uniformly accelerated motion) and bass fall (internal resistance). In his theory he combined mathematical abstraction with physical reality, key to understanding the laws of nature. He was crystal clear about this fact and expressed it in concrete numerical examples. He classified the different types of movement in:

Uniform movement over time:

It is the one by which the same mobile in equal intervals of time travels equal distances, as is perfectly given in the extremely regular motion of the sky.

Movement disagrees over time:

It is the one by which, in different parts of time, uneven distances are traveled, or in (times) uneven, (spaces) equal.

Movement evenly disformed over time:

It is the movement in such a disforming way, that if we divide according to time, (the speed of) the midpoint of the ratio exceeds (the speed of) the slowest end what is exceeded by the fastest.

The movement evenly dissimilar to time is the one whose diformity is such, that if it is divided according to time, that is, according to the parts that occur in time, in every part of the movement of the central point exceeds the extreme movement the least of that same part in quantity equal to that in which he himself is overcome by the most intense extreme movement.

Soto described the movement of free fall as an example of uniformly accelerated movement for the first time, an issue that would only appear later in Galileo's work:

[...] this kind of movement properly happens in the naturally moved (graves) and in the projectiles. Where a weight falls from above by a uniform medium, it moves faster in the end than in the beginning. However, the movement of the projectiles is slower at the end than at the beginning: the first increases evenly disformed, and the second instead decreases evenly diform.

Therefore, the law of average velocity was applicable to calculate the fall time:

This kind of movement is one of the bodies that move with natural movement and that of the projectiles.

In fact, every time a mass falls from a certain height and within a homogeneous medium, it moves at the end more in a hurry than at the beginning. But the movement of the projectiles is slower at the end than at the beginning, and so the first is intensified, and the second is weakened evenly.

Differently warp motion with respect to time:

It is the movement in such a disforming way, that if it is divided according to time, it does not occur that the midpoint of each part in the same proportion exceeds (at speed) to one end as it is exceeded by the other. This type of movement is the one we expect in the animals, where the increase and the decrease are observed.

Portrait of Galileo Galilei

This was a key discovery in physics and an essential foundation for the later study of gravity by Galileo Galilei and Isaac Newton. No scientist at the Universities of Paris and Oxford at the time had succeeded in describing the relationship between uniform time warp motion and bass decay as Soto did.

Following these scientists' groundbreaking ideas about motion, Galileo made a major breakthrough by introducing the scientific method which teaches that one should not always believe intuitive conclusions based on immediate observation, as this often leads to mistakes. Galileo carried out a large number of experiments in which the conditions of the problem were slightly changed and he measured the results in each case. In this way, he was able to extrapolate his observations to understand an ideal experiment, specifically, he observed how a body that moves with constant speed on a smooth surface will move forever if there is no friction or other external actions on it.

Immediately another problem arose: if speed does not reveal it, what movement parameter indicates the action of external forces?; Galileo also answered this question, but Newton did it in a more precise way: it is not the speed but its variation that results from the action of dragging or pushing an object. This relationship between force and change of velocity (acceleration) constitutes the fundamental basis of classical mechanics. Isaac Newton (circa 1690) was the first to give a complete formulation of the laws of mechanics and invented the necessary mathematical procedures to explain them and obtain information from them.

Limitations and further generalizations

After Newton formulated the three famous laws, numerous physicists and mathematicians made contributions to give them a more general form or easier application to non-inertial systems or systems with constraints. One of these first generalizations was d'Alembert's principle of 1743, which was a valid form for when there were ligatures that allowed the equations to be solved without the need to explicitly calculate the value of the reactions associated with said ligatures.

Around the same time, Lagrange found a form of the equations of motion valid for any inertial or non-inertial reference frame without the need to introduce fictitious forces. Since it is a known fact that Newton's Laws, such as were written, they are only valid for inertial reference frames, or more precisely, to apply them to non-inertial frames, they require the introduction of so-called fictitious forces, which behave like forces but are not directly caused by any material particle or agent. concrete, but are an apparent effect of the non-inertial reference frame.

Later, the introduction of the theory of relativity made it necessary to modify the form of Newton's second law (see (2c)), and Quantum mechanics made it clear that Newton's laws or general relativity are only approximations to dynamic behavior on macroscopic scales. Some macroscopic and non-relativistic modifications have also been conjectured, based on other assumptions such as MOND dynamics.

Relativistic Generalizations

Newton's laws are three principles approximately valid for small speeds. The way in which Newton formulated them was not the most general possible. In fact the second and third laws in their original form are not valid in relativistic mechanical theory of relativity however formulated in a slightly different way the second law is valid, and the third law admits a less restrictive formulation that is valid in relativistic mechanics.

First Lawin the absence of gravitational fields does not require modifications. In a flat space-time a straight line fulfills the condition of being geodetic. In the presence of curvature in space-time, Newton's first law remains correct if we replace the straight line expression by geodetic line.
Second Law. It remains valid if the force on a particle is said to match the rate of change of its linear moment. However, now the definition of linear moment in Newtonian theory and relativistic theory differ. In Newtonian theory the linear moment is defined according to (1a) while Einstein's relativity theory is defined by (1b(c):

(1a) ${mathbf {p}}=m{mathbf {v}}$

(1b) ${mathbf {p}}={cfrac {m{mathbf {v}}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}$

where m is the invariant mass of the particle and

{mathbf {v}}

the speed of this measure from a certain inertial system. This second formulation of fact implicitly includes definition (1) according to which the linear moment is the product of the mass by speed. As that implied assumption is not fulfilled within the framework of Einstein's relativity theory (where the definition is (2)), the expression of force in terms of acceleration in the theory of relativity takes a different form. For example, for the rectilinear motion of a particle in an inertial system the expression equivalent to (2a) is:

(2b) ${mathbf {F}}=m{mathbf {a}}left(1-{frac {v^{2}}{c^{2}}}right)^{{-{frac {3}{2}}}}$

If speed and force are not parallel, the expression would be as follows:

(2c) ${mathbf {F}}={frac {m{mathbf {a}}}{(1-{frac {v^{2}}{c^{2}}})^{{{frac {1}{2}}}}}}+{frac {m({mathbf {v}}cdot {mathbf {a}}){mathbf {v}}}{c^{2}(1-{frac {v^{2}}{c^{2}}})^{{{frac {3}{2}}}}}}$

Note that this last equation implies that except for the rectilinear movement and the uniform circular, the acceleration vector and the force vector will not be parallel and will form a small angle related to the angle that form the acceleration and speed.

Third Law. The original formulation of the third law by Newton implies that the action and reaction, besides being of the same magnitude and opposite, are colinear. In this way the third law is not always fulfilled in the presence of magnetic fields. In particular, the magnetic part of Lorentz's force that is exercised by two moving particles are not equal and of an opposite sign. This can be seen by direct compute. Two punctual particles with loads q₁ and q₂ and speeds ${mathbf {v}}_{i}$ , the strength of particle 1 on particle 2 is:

${mathbf {F}}_{{12}}=q_{2}{mathbf {v}}_{2}times {mathbf {B}}_{1}={frac {mu q_{2}q_{1}}{4pi }} {frac {{mathbf {v}}_{2}times ({mathbf {v}}_{1}times {mathbf {{hat {u}}}}_{{12}})}{d^{2}}}$

where d the distance between the two particles and ${mathbf {{hat {u}}}}_{{12}}$ is the unit director vector that goes from particle 1 to 2. Similarly, the strength of particle 2 on particle 1 is:

${mathbf {F}}_{{21}}=q_{1}{mathbf {v}}_{1}times {mathbf {B}}_{2}={frac {mu q_{2}q_{1}}{4pi }} {frac {{mathbf {v}}_{1}times ({mathbf {v}}_{2}times (-{mathbf {{hat {u}}}}_{{12}}))}{d^{2}}}$

Employing vectorial identity ${displaystyle mathbf {a} times (mathbf {b} times mathbf {c})=(mathbf {a} times mathbf {c})times mathbf {b} =(mathbf {a} times mathbf {b})times mathbf {c} }$ , it can be seen that the first force is on the plane formed by ${mathbf {{hat {u}}}}_{{12}}$ and ${mathbf {v}}_{1}$ that the second force is on the plane formed by ${mathbf {{hat {u}}}}_{{12}}$ and ${mathbf {v}}_{2}$ . Therefore, these forces do not always turn out to be on the same line, nor in general they are of equal magnitude. This example of two moving charged particles that interact with each other (expressed in a classic non-relativist way), is known as the Feynman paradox. And it is solved taking into account the equations of the Relativist Electrodynamic for the fields and particles

Ehrenfest's Theorem

Ehrenfest's theorem allows us to generalize Newton's laws to the framework of quantum mechanics. Although in this theory it is not lawful to speak of forces or trajectories, one can speak of magnitudes such as linear momentum and potential in a similar way to what is done in Newtonian mechanics.

Specifically, the quantum version of Newton's second Law states that the time derivative of the expected value of the momentum of a particle in a field equals the expected value of the "force" or expected value of the gradient of the potential:

${displaystyle {begin{aligned}{frac {d}{dt}}langle prangle =&int Phi ^{*}V(x,t)nabla Phi ~dx^{3}-int Phi ^{*}(nabla V(x,t))Phi ~dx^{3}-int Phi ^{*}V(x,t)nabla Phi ~dx^{3}\{}=&;0-int Phi ^{*}(nabla V(x,t))Phi ~dx^{3}-0\{}=&;langle -nabla V(x,t)rangle =langle Frangleend{aligned}}}$

Where:

V(x,t),

is the potential of which to derive “forces”.

PhiPhi ^{*},

, are the wave functions of the particle and its complex conjugate.

nabla ,

denotes the operator.

Contenido relacionado

Más resultados...