Neperian abacus

Neperian abacus

Napier's abacus is an abacus invented by John Napier who published the description of it in a work printed in Edinburgh at the end of 1617 entitled Rhabdologia. By this method, the products are reduced to operations of addition and the quotients to subtractions; As with the tables of logarithms, invented by himself, powers are transformed into products and roots into divisions.

Description

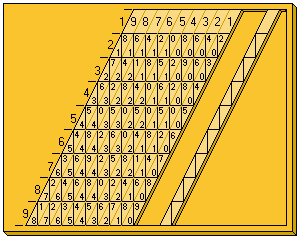
The abacus consists of a board with a rim on which the Neperian rods will be placed to carry out multiplication or division operations. The board has its left edge divided into 9 squares in which the numbers 1 to 9 are written.

The Neperian rods are strips of wood, metal or thick cardboard. The front face is divided into 9 squares, except for the upper one, divided into two halves by a diagonal line.

In the first box of each rod, write the number, filling the following ones with the double, triple, quadruple and so on until the nine times the number to which the rod corresponds.

The digits resulting from the product are written one on each side of the diagonal and in those cases in which it is less than 10, they are written in the lower box, writing a zero in the upper one.

A set consists of 9 rods corresponding to the digits 1 to 9. The figure also represents rod 0, which is not really necessary for the calculations.

Multiplication

Given the set described, suppose we want to calculate the product of the number 46785399 by 7.

On the board we will place the rods corresponding to the number, as shown in the figure, subsequently reading the result in the horizontal band corresponding to 7 of the box on the board, an operation that only requires simple additions, naturally with carrying of the digits located diagonally.

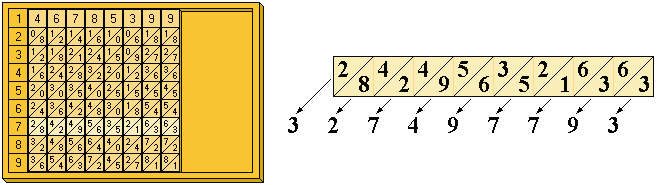
Starting from the right we will obtain the units (3), the tens (6+3=9), the hundreds (6+1=7), etc.

If any digit of the number we want to multiply were zero, it would suffice to leave a gap between the rods.

Suppose we want to multiply the previous number by 96,431; operating analogously to the previous case we will quickly obtain the partial products of the number by 9, 6, 4, 3 and 1, placing them correctly and adding, we will obtain the total result.

Division

Equally, divisions could be made once the 9 partial products of the dividend are known; Once these have been determined using the abacus, it is enough to select the one immediately below the rest without the need to carry out the annoying trial and error that divisions made by hand require.

In the example, to do the previous operation, the following method is followed:

• The dividend (46.785.399) has eight digits and the divider (96.431) has five. Therefore, the quotient will have 8 - 5 = 3 digits. At most, the quotient could have 8 - 5 + 1 = 4 digits, but since it is 4 of the dividend smaller than 9 of the divisor, the quotient is 3 digits. These issues belong to arithmetic.

That makes it necessary to move the 3 - 1 = 2 digits of the dividend, remaining the number 467.853 as the minuendo to which the proper substraendo must be sought.

Using the neperian board obtained, the smaller number closer to 467.853 is sought, which turns out to be 385.724, which is substrating the operation and whose associated number in the neperian table is the 4, number that forms part of the quotient. The result of the subtraction is 82,129.

• The resulting number (82.129) is added a nine that had previously been despised, remaining 821.299.

Again, the subtraction operation must be performed at 821,299 (low) with the nearest substraendo of the neperian table, which is 771,448, whose associated number is eight and whose subtraction is 49,851.

• The nearest number, which is 482,155, whose associated number is five. The subtraction results in 16,364.

• Since 16,364 is less than any of the numbers on the Neperian table and, in addition, the three digits of the quotient have already been obtained: 4, 8 and 5, the rest of the operation has already been obtained.

The result is therefore the following (as can be seen in the table):

Name	Value
Split	46.785.399
Split	96.431
Patient	485
Resto	16.364

Square root

As we know, to extract a square root first, the digits must be grouped two by two from the comma, both to the right and to the left, leaving the number as follows:

... xx xx xx xx, xx xx xx...

For example: the number 458938.34 would be 45 89 38, 34.

Taking the pair (which may be a single digit) on the left (xx), the integer number a is obtained such that its square is equal to or less than the pair. This will be the first digit of the solution. Subtracting from the pair the square of the integer thus found, we obtain the remainder:

r_a = xx - a2 (If the first pair was 07, the number would be 2, and the rest 7-4=3)

Later, and iteratively, the following pair is added to the remainder, leaving a number of the form yxx (y, the previous remainder, xx the added pair) that we will call Ra. The next digit of the solution must be such that the square of the partial solution ab (ab being a two-digit number, not a product) is less than xxxx (the first two pairs of the radicand):

(ab)2 = (a·10 + b)2 = (a·10)2 + 2·a·10·b + b2, xxx

Clearing:

2·a·10·b + b2 ك xxx - (a·10)2 = R

(2·a·10 + b)·b θ (I)

Operating in the same way once the digits ab are known, the third digit of the solution (c) and the following digits (d, e,...) must be determined, which, as can easily be demonstrated by operating analogously to the previous case, must achieve:

(2·(ab)·10 + c)·c  Rb (II)

(2·(abc)·10 + d)·d θ (III)

(2·(abcd)·10 + e)·e  Rb (IV)

...

The indicated products can be easily obtained with Napier's abacus, but for this an auxiliary rod is necessary so that in each horizontal strip it collects the squares of the corresponding numbers.

Once the first number a is known, we place the rod(s) corresponding to the double of a on the abacus. Once this is done, it will suffice to add the rod of the squares to find the number such that equation (I) is fulfilled, which will be the one corresponding to the band b. This number must be subtracted from Ra to find Rb.

Once b is found, we remove the auxiliary rod from the squares and place the rod corresponding to 2·b on the board; Two cases can occur, if b is less than 5, the double will have only one figure with which it will be enough to place the rod; otherwise (equal to or greater than 5) the double will be greater than 10, so it will be necessary to increase the last rod placed by one unit.

Let's see it with an example. We wish to obtain the square root of the number 46 78 53 99. We take the first pair (46) and determine the immediately lower square, which turns out to be 36 (49 which is the next is greater than 46), so that the first digit of the number solution is 6, and the remainder: 46 - 6 6 = 46 - 36 = 10.

We place the rods of 6·2 = 12 on the board, and then the auxiliary rod of the squares. We compose the remainder and the following pair obtaining the number 1078 that should not be exceeded by the square of (6b). We read in the abacus (1) the value 1024, finding that b= 8 and the new remainder 1078 - 1024 = 54, descending the next pair, we obtain a value of 545312.

We place the rods corresponding to the double of 8; Since it is 16 (>10), we will remove the last rod, the one for 2, replacing it with the one for 3 (that is, we add one unit) and add the rod for 6. The abacus remains as shown in (2a). As it can be observed, the figures placed are those corresponding to double the solution found so far (68·2 = 136); that is, the 2abc of the previous equations.

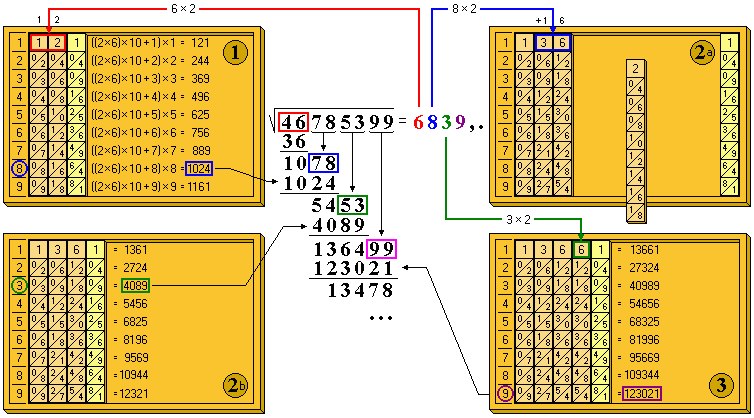
Once this is done, we replace the auxiliary rod, and operating as in the previous case, we obtain (2b) the third figure: 3, the rest being 1364. We descend the following pair obtaining a value 136499, we place the rod 6 (3·2) and find the next digit 9 and the remainder 13478. As long as the remainder is different from zero, we can continue obtaining significant figures.

For example, to obtain the first decimal, we would lower the pair 00 obtaining the number 1347800 and we would place the rods of 9·2 = 18, leaving the following on the board: 1-3-6-7(6+1) -8-auxiliary. Doing the check, we get the first decimal = 9.

Modifications

During the 19th century, the Neperian abacus underwent a transformation to make it easier to read. The rods began to be manufactured with an inclination of the order of 65º, so that the triangles that had to be added would be vertically aligned. In this case, in each box of the rod, the unit is recorded on the right and the ten (or zero) on the left.

The rods were made in such a way that the vertical and horizontal engraving was more visible than the joints between the rods, making reading much easier as the pair of components of each digit of the result remained in a rectangle.

Thus, in the figure it is immediately apparent that:

987654321 x 5 = 4938271605

Abacus of tiles

Abbey of the National Archaeological Museum, Madrid

Detail

In addition to the above abacus, Napier constructed a token abacus. Both gathered in a single device constitute a historical jewel, unique in Europe, which is owned by the Spanish National Archaeological Museum.

The apparatus is a magnificent wooden box inlaid with bone. In the upper part it contains the rhabdological abacus, while in the lower part there is the second abacus that consists of 300 cards stored in 30 drawers, of which 100 are covered with figures and two hundred show small triangular holes that allow only certain figures of the number cards when they overlap those, in such a way that thanks to the skilful placement of one and the other, multiplications can be carried out up to the astonishing limit of a number of 100 figures by another of 200.

The first powers of the digit numbers, the coefficients of the terms of the first powers of the binomial and the numerical data of the regular polyhedra are also found on the doors of the box.

It is unknown who the author of this extremely rich jewel was, nor if it was made in Spain or came from abroad, although it is likely that it originally belonged to the Academy of Mathematics created by Felipe II or that the Prince of Wales brought it as a gift. The only thing that can be assured is that it was kept in the Palace, from where it went to the National Library and later to the National Archaeological Museum, where it is still kept.

In 1876, the Spanish government sent the apparatus to the exhibition of scientific instruments held in Kensington, where it attracted extraordinary attention, to the point that various societies consulted the Spanish representation about the origin and use of the apparatus, which motivated D. Felipe Picatoste to write a monograph that was later sent to all nations, surprising the fact that the abacus was only known in England, the country of origin of its inventor.