Mollweide projection

Mollweide Projection.

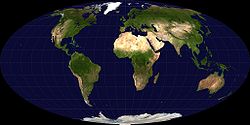
The Mollweide projection, also known as the Babinet, is a pseudocylindrical, equal mapping projection, generally used for maps of the Earth or the night sky.

The projection was first published by the mathematician and astronomer Karl Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name of the homalographic projection.

Its purpose is to represent the ratio of areas as accurately as possible.

Properties

Mapmundi represented using Mollweide projection.

The equator is twice as long as the short axis, the central or type meridian, is straight. Meridians at 90° are circular arcs. The parallels are straight but unequally spaced. The scale is false only along the standard parallels of 40:44N and 40:44S, so it has a greater representation by the equatorial zone. The Mollweide projection is used for world maps, especially to represent low latitude areas.

Mathematical formulation

Latitude and longitudes in x and y coordinates by means of the following equations:

${displaystyle x=R{frac {2{sqrt {2}}}{pi }left(lambda _{0}right)cos left(theta right),}}$

${displaystyle y=R{sqrt {2}}sin left(theta right),,}$

where θ is an auxiliary angle defined by

${displaystyle 2theta +sin left(2theta right)=pi sin left(varphi right)qquad (1)}$

y λ is longitude, λ₀ is the central meridian, φ is latitude, and R is the radius of the balloon to be projected. The map has an area of 4πR², according to the surface of the generating globe. The x coordinate has a range of [−2R√2, 2R√2], and the y coordinate has a range of [−R√2, R√2].

Equation (1) can be solved with fast convergence (but slow near the poles) using the iteration of the Newton–Raphson Method:

${displaystyle theta _{0}=varphi,}$

${displaystyle theta _{n+1}=theta _{n}-{frac {2theta _{n}+sin left(2theta _{n}right)-pi sin left(varphi right)}}{2+2cos left(2theta _{n}right)}}}}}}}}.$

If φ = ±π/2, then also θ = ±π/2. In that case iteration should be avoided; otherwise, it could result in division by zero.

There is a closed form of inverse transformation:

${displaystyle varphi =arcsin left[{frac {2theta +sin left(2theta right)}{pi }}{right],,}$

${displaystyle lambda =lambda _{0}+{frac {pi x}{2R{sqrt {2}}cos theta },,}$

where θ can be found by the relation

${displaystyle theta =arcsin left({frac {y}{R{sqrt {2}}}right}.$

Inverse transformations allow you to find the latitude and longitude corresponding to the x and y coordinates.