Millikan's experiment

Millikan installation for the oil drop experiment.

The oil drop experiment was performed by Robert Millikan and Harvey Fletcher in 1912 to measure elementary charge (the charge of an electron).

This experiment involved balancing the gravitational force (directed downwards) with the buoyancy (directed away from gravitational) and electrical forces in the tiny charged oil droplets suspended between two strongly accelerated metal electrodes. Since the density of the oil was known, the masses of the 'droplets', and thus their gravitational and buoyant forces, could be determined from their observed radii. Using a known electric field, Millikan and Fletcher were able to determine the charge on the oil droplets in mechanical equilibrium. Repeating the experiment for many drops, they confirmed that the charges were all multiples of a fundamental value, and calculated that it is 1.5924|(17).10^-19 C, to within one percent of positive of the currently accepted value of 1.602176487|(40).10^-19 C. They proposed that this was the charge of a single electron.

Base

Robert Millikan in 1891.

Beginning in 1915, while a professor at the University of Chicago, Millikan, with important input from Fletcher, worked on the oil-drop experiment, which measured the charge of a single electron. After a publication of his first results in 1910, the conflicting observations of Felix Ehrenhaft started a controversy between the two physicists. After improving his experimental setup, he published his seminal study in 1913.

His experiment measures the intensity of the electrical force against the force of gravitational attraction in the tiny drops of oil, charged by friction, suspended between two metal electrodes. Knowing the electric field, the charge on the drop is determined. Repeating the experiment for many drops, Millikan showed that the results could be explained as integer multiples of a common value 1.592x10^-19 C, the charge of a single electron.

At the time of Millikan and Fletcher's oil drop experiments, the existence of subatomic particles was not universally accepted. Experimenting with cathode rays, Thomson discovered in 1897 negatively charged corpuscles (as he called them), with a mass about 1800 times smaller than that of a hydrogen atom. Similar results had been found by George Francis FitzGerald and Walter Kaufmann. Most of what was then known about electricity and magnetism, however, could be explained on the grounds that charge is a continuous variable, just as many of the properties of light can be explained by treating it as a continuous wave rather than as a stream of photons.

The so-called elementary charge e is one of the fundamental physical constants and its exact value is of great importance. In 1923 Millikan won the Nobel Prize in Physics partly for this experiment.

Measurement aside, the beauty of the oil drop experiment is that it is a simple and elegant practical demonstration that charge is actually quantized. Thomas Edison, who had considered charge as a continuous variable, became convinced after working with the Millikan and Fletcher apparatus. This experiment has been repeated by generations of physics students, although it is quite expensive and difficult to do correctly.

Experimental procedure

Simplified scheme of Millikan oil drop experiment.

Robert Millikan's apparatus incorporates a pair of horizontal parallel metal plates. By applying a potential difference between the plates, a uniform electric field is created in the space between them. A ring of insulating material was used to keep the plates apart. Four holes were cut in the ring, three for illumination with a bright light, and one to allow viewing through a microscope.

A fine mist of oil droplets is sprayed into a chamber above the plates. The oil was of a type normally used in vacuum apparatus and was chosen because it had extremely low vapor pressure. Ordinary oil would evaporate under the heat of the light source causing the mass of the oil drop to change over the course of the experiment. Some oil droplets became electrically charged through friction with the nozzle when sprayed, while others discharged to become cations and others became neutral. Alternatively, charging could be accomplished by including a source of ionizing radiation (such as an X-ray tube).

Method

A scheme of the apparatus of the experiment of the drop of the oil drop. En: The Electron: Its Isolation and Measurements and the Determination of Some of its Properties, Robert Andrews Millikan, 1917.p. 109.. Legend: D = bronze container; m = mercury manometer; w = 80 cm long water cell; d = copper chloride cell; A= bow; M & N = condensation plates; G: immersion tank of the container D in a 40 l gas-oil bath to keep the temperature constant; A = atomizer; e= air input.

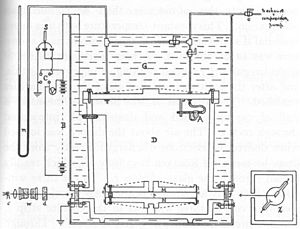
Initially the oil droplets are dropped between the plates with the electric field turned off. Very quickly they reach terminal velocity due to friction with the air in the chamber. The field is then turned on, and if it is large enough, some of the droplets will start to rise. (This is because the upward electrical force F_E is greater than the downward gravitational force F_g). One drop is selected to observe the likely fall and is held in the center of the field of view by alternately turning the voltage on and off until all other drops have fallen. The experiment is then continued with this single drop.

The drop is dropped and its terminal velocity v₁ is calculated in the absence of an electric field. The friction force acting on the drop can be calculated using Stokes' law:

Fd=6π π rMIL MIL v1{displaystyle F_{d}=6pi reta v_{1},}

where v₁ is the terminal velocity (i.e., the velocity in the absence of electric field) of the falling drop, η is the viscosity of air, and r is the radius of the drop.

The weight F_g is the volume V multiplied by the density ρ and the acceleration due to gravity g. However, what is needed is the apparent weight. The apparent weight in air is the actual weight minus the weight of the air displacing the drop (upthrust). For a perfectly spherical drop the apparent weight can be expressed as:

W=43π π r3g(ρ ρ − − ρ ρ air){displaystyle W={frac {4}{3}}pi r^{3}g(rho -rho _{air}),}

At terminal velocity, the oil drop is not accelerating. Thus the total force acting on it must be zero. Thus the two forces F_d and F_g must cancel each other (that is, F _d = F_g). This implies that:

r2=9MIL MIL v12g(ρ ρ − − ρ ρ air).{displaystyle r^{2}={frac {9eta v_{1}}}{2g(rho -rho _{air}}}}}}.

Once r has been computed, F_g can be easily computed.

Now the field is turned back on, and the electric force on the drop is:

FE=qE{displaystyle F_{E}=qE,}

where q is the charge on the oil drop and E is the electric field between the plates. For parallel plates:

E=Vd{displaystyle E={frac {V}{d}}{,}

where V is the potential difference and d is the distance between the plates.

One of the conceivable ways to calculate q would be to adjust V until the drop of oil remains stable. Then we could equate F_E with F_g. But in practice this is very difficult to do accurately. Furthermore, the determination of F_E is difficult because the mass of the oil drop is difficult to determine without reverting back to the use of Stokes' Law. A more practical approach is to make V up a bit larger so that the oil drop rises with a new terminal velocity v₂. So:

qE− − Fg=6π π rMIL MIL v2=Fgv2v1.{displaystyle qE-F_{g}=6pi reta v_{2}={frac {F_{g}{v_{2}}{v_{1}}}}}.

Fraud accusations

There is some controversy raised by historian Gerald Holton about the use of selectivity in Millikan's results from his second experiment for the measurement of electron charge. Holton (1978) noted that Millikan discarded a large set of oil droplets obtained in his experiments for no apparent reason. Allan Franklin, a former high-energy researcher and current philosopher of science at the University of Colorado has tried to refute Holton's point. Franklin claims that Millikan's exclusions of data do not affect the final value of e which Millikan got, but admits there was substantial "facelift" which Millikan performed and which had the effect of reducing the statistical error in e. This allowed Millikan to cite that he had calculated e with an error of less than a mean of one percent, in fact, if Millikan had included all the data he obtained, it would have been 2%. Although all of this might have translated to Millikan having measured the value of e better than anyone else at the time, the slightly larger uncertainty might have allowed for more disagreement with his results in the physics community. David Goodstein recounts that Millikan clearly states that he only included the drops that had been subjected to "a complete series of observations"; and he did not exclude any drop from this group.

Millikan's experiment and pseudoscience

In a keynote address given at the California Institute of Technology (Caltech) in 1974 (and reprinted in Are you kidding, Mr. Feynman?), physicist Richard Feynman noted:

We have learned a lot from the experience about how to handle some of the ways we deceive ourselves. One example: Millikan measured the load of an electron in an oil drop-down experiment, and received an answer that we now know is wrong. He's a little grabbed by the hairs because he had the wrong value for the air viscosity. It is interesting to observe the history of the measurements of the load of an electron, after Millikan. If a chart of the measurement of the load is drawn depending on the time, it is discovered that a data is a little larger than that of Millikan, and the next one is a little bigger than that, and the next one is a little bigger than that, until they finally settle in a larger number.

Richard Feynman

Why didn't they find out that the new number was the immediate superior? It is something that scientists are ashamed of - of this story - because it is evident that people thought things like this: When they came to a number that was too high above Millikan, they thought something should be wrong - and they searched and found a reason why something might be wrong. When they reached a number close to Millikan's value, they didn't find it that difficult. And so they removed the numbers that were too far away, and other things like that. We've learned those tricks today, and now we don't have that kind of evil.

Richard Feynman

As of 2008, the accepted value for the elementary charge is 1.602176487|(40).10^-19 C, where 40 indicates uncertainty in the last two figures. In his Nobel lecture, Millikan gave his measurement as 4.774(5).10^-10 uec, which is equal to 1.5924(17).10^-19 C The difference is less than one percent, but it is more than six times the Millikan standard deviation, so the disagreement is significant.

Further reading

• Serway, Raymond A.; Faughn, Jerry S. (2006). Holt: Physics. Holt, Rinehart and Winston. ISBN 0-03-073548-3.
• Thornton, Stephen T.; Rex, Andrew (2006). Modern Physics for Scientists and Engineers (3rd ed.). Brooks/Cole. ISBN 0-495-12514-8.
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
• — PDF (in English) Millikan article of 1913 On the elementary electrical charge and the avogadro constant, archived in archive.org
• — PDF (in English) Presentation of Millikan during the Nobel Prize award ceremony in 1923: The electron and the light-quant from the experimental point of view, filed in archive.org