Microeconomics

Microeconomics is a part of economics that studies the economic behavior of individual agents, such as consumers, companies, workers and investors; as well as their interrelation in the markets. Consider the decisions each one makes to meet certain goals of their own. The basic elements on which microeconomic analysis focuses are goods, prices, markets and economic agents. In contrast, macroeconomics is the part of economic theory that deals with the general study of the economy, through the analysis of aggregate variables such as the total amount of goods and services produced, the level of employment, the balance of payments, the exchange rate and the general behavior of prices.

History

The difference between microeconomics and macroeconomics was introduced in 1933 by the Norwegian economist Ragnar Frisch, co-recipient of the first Nobel Prize in Economic Sciences in 1969. However, Frisch did not actually use the word "microeconomics" 34;, but made distinctions between "micro-dynamic" and "macro-dynamic" in a similar way to how the words "microeconomics" and "macroeconomics". The first known use of the term in a published paper was by Pieter de Wolff in 1941, who expanded the term "micro-dynamics" to "microeconomics".

Branches

The supply and demand model describes how prices vary according to the balance between product availability at different prices (offer) and the wishes of those with purchasing power according to the price (demanda). The chart shows a scroll to the right of D₁ a D₂ with the corresponding increase in the price and quantity required to achieve a new balance point in the market in the supply curve (S).

Microeconomics has several branches of development, of which partial equilibrium, general equilibrium and Nash equilibrium stand out to understand consumer and producer problems in goods and services markets.

These branches or sub-disciplines cannot be considered entirely separate because the results of some aspects influence others (in particular, general equilibrium theory speaks of the interaction between them). For example, companies not only offer goods and services, but also demand goods and services in order to produce their own. Microeconomics proposes mathematical models that develop certain assumptions about the behavior of economic agents, the conclusions reached using these models will only be valid, as long as the assumptions are met, which rarely happens, especially if deals with very strong or restrictive assumptions.

One of the most important additions to the study of microeconomics is the Nash equilibrium, as a solution concept to the proposed games. Game theory is a mathematical theory that studies the behavior of various agents when the decisions made by each one influence the decisions of the others.

Despite the successes of neoclassical microeconomic theory in understanding some of our economic problems, it does not understand them all because in these models the institutional relations of societies are practically absent, beyond the markets of goods and services. When assessing its scope and limits, it could be said that neoclassical theory is like Taylor's first polynomial, it is a first approximation, valuable but insufficient. There is hope that recent advances in "institutional microeconomics" and "microeconomics of complex economies" will provide a better understanding of the role of institutions, evolution and learning in the behavior of agents inside and outside the markets.

Consumer theory

In what follows and, unless otherwise stated later, everything said will refer to the theory of the consumer to the dominant neoclassical theory. The neoclassical consumer theory is based on preferences that an individual has. Based on them, the consumer will make a rational choice between the available goods and those that he can acquire with his budget.

Consumer preferences

Consumers have preferences on goods and services, that is, given baskets of goods (sets of goods and services that an individual consumes, in which, of each type of good, there can be zero, one or another quantity of goods, even a non-integer amount), if given a choice between two bundles, a consumer will prefer one over the other (he may also be indifferent between them).

It is assumed, then, that for the majority of consumers there will be some preferences that they could manifest for any set of baskets that are presented to them. Each individual will have his preferences and they would not have to coincide with those of another subject, although it could be so. However, it is expected that for the majority of consumers these preferences do have some common properties. The theory of consumer behavior is based on these assumptions or basic properties of the preferences of individuals for one basket over another, which are exposed. So if these conditions were not met, the conclusions drawn in consumer theory would not be fully valid. These properties would be:

• Completion: the consumer could classify all types of baskets, i.e. all sets of indifference have no fissures.
• UniversalityGiven any pair of baskets imaginable in an economy, a consumer could always say if he prefers one basket to another. Note that it is also possible that you cannot consider a basket really better than the other, but you are expected to say that a basket is at least as good as the other. That is, it will not be necessary that the preference is always strict, but given any two baskets, the consumer can always say, or that the same gives him the one that the other, or that considers one of the two better than the other.
• Transitivity: Generally, if a consumer prefers basket A to basket B, and basket B to C, you should also prefer basket A to C.
• Monotony or the more, the better: If a basket A has the same goods as another basket B, and some more, or more of any of them, then A is preferred or considered at least as good as B. Consequently, consumers always prefer a greater amount of any good to a minor.
• Convexity: It is expected, although this assumption is somewhat restrictive, that given two baskets A and B of goods, both are preferred a basket C that was a convex combination of both. That is to say, a basket that is composed in a percentage of the quantities of each of the goods present in A and in the rest of the percentage (up to 100%) of the quantities of B goods. This assumption is related to the decreasing marginal utility principle.

Budget Constraint

Taking into account that goods have prices, and considering these data, it is clear that a consumer cannot trivially get the basket that he prefers among all the possible ones. If we take into account, in addition to the prices of goods, the consumer's disposable income, we have what is called the budget constraint. This is what tells us which baskets of goods are the ones that the consumer can choose and get, taking into account the money he has available and market prices. The consumer's mission will then be to find, among all these baskets, the one that he prefers to all the others (or one of the baskets that he considers to be at least as good as all the others). Finding this is what is called consumer maximization. Generally, it is common for the consumer's chosen bundle to be on the budget constraint frontier, that is, to be a bundle whose value (multiplying the prices of the goods by the quantities of these in the bundle) is exactly equal to the consumer disposable income. Therefore, the consumer will always choose the basket that provides the maximum utility, the one that produces the greatest possible well-being.

Utility function

One way to represent preferences, when they have the right properties, is by what is called a utility function. In this case, the baskets of goods can also be represented as numerical vectors, where each component of the vector tells us how much of each good is in that basket. By introducing two vectors of goods into the same utility function and seeing what numbers it returns, it is possible to see if one basket is preferred over the other or considered equal to the other from the consumer's point of view. Then, the consumer problem could be considered as the mathematical problem of maximizing a mathematical function (often of several variables), which would be the utility function, within the set represented mathematically by all baskets of goods (vectors) that meet the restriction budgetary, that is, that its value (result of multiplying the vector of goods in the basket by the vector of the corresponding prices) was equal to or less than the value of disposable income.

Note that the utility function is considered a monotonic increasing function of goods, but that its value is purely ordinal, that is, it serves to order baskets but not to say how much better a basket is than another, that is, it is not a cardinal function. In fact, different utility functions can be used to represent the same preferences, and when solving the maximization problem they would all give the same result.

Indifference Curves

This section is a Curva extract of indifference.[chuckles]edit]

Figure 1. An example of indifference map with two eligible goods X and Y and three indifference curves, that is, three different levels of satisfaction.

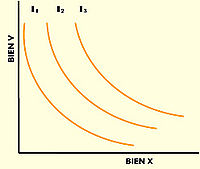
In microeconomy the indifference curves (also called preference curves) are combinations of goods, represented as sets of points in space, for which the satisfaction of a consumer is identical. This means that for all points belonging to the same curve, the consumer has no preference for one combination or another. Consumer satisfaction is characterized by the utility function, where the variables are the amounts of each good, represented by the value on each axis.

Consumer preferences allow you to choose between different consumer baskets. If you offer a consumer two different baskets, you will choose the one that best suits your tastes. If both satisfy their tastes to the same extent, it is said that the consumer is "indifferent" between the two baskets. There are discrepancies between authors about whether the continuity, derivability and convexity of such curves are guaranteed and this has strong implications in the discussion of the existence or not of balance points. From a mathematical point of view the discussion implies the axiom of choice.

Figure 2. Deduction of indifference curves. First, it is shown that the marginal utility is decreasing compared to the two variables (requirement for the curves to be convex and balance). Below is a representation of the function in which Z is the utility. Finally the level curves are projected on the XY plane.

The most common graphic representation presents two alternative properties X and Y (Figure 1), among which the consumer can choose. The points of each curve represent the combinations of X and Y goods that provide the same utility to the consumer.

Another issue of importance in the study of consumer theory are the so-called indifference curves. An indifference curve would represent all bundles that have the same value for a given utility function.

The main use of indifference curves is to find the utility maximization points by superimposing them with the consumer's budget constraints, which define the points available to each individual depending on their availability in monetary units.

On the other hand, the marginal rate of substitution tells us how much a consumer is capable of exchanging one good for another so that its utility remains the same.

Types of goods

You can study how the solutions to the consumer's problem change when the parameters of the utility function change or the consumer's prices or disposable income change. For example, if the price of one of the goods changes, the change in the slope of the budget constraint will lead to a change in the chosen bundle of goods, in which the good whose price has changed will also change in quantity (and possibly the quantity of goods). other of the goods also change). Depending on the effect that occurs, goods can be classified. Thus, normally goods decrease in quantity demanded when their price increases, although there are exceptions to this, in which they increase (called Giffen goods). What makes a good change is the sum of two effects, the income effect and the substitution effect.

The income effect is derived from the fact that by increasing a price, in a certain way, it is as if income were lost, while the substitution effect is related to how the consumer may tend to substitute the consumption of a good for that of another If the price of the good increases, the income effect will tend to decrease its consumption, but the substitution effect can affect it in two ways. Normally it will tend to make it also decrease, because the consumer is also going to consume other types of goods whose price has not changed, but on other occasions it could make it increase. Naming the above in Marshallian terms, we can say that the value of the succeeded merchandise is replaced by equivalent money, thus achieving that the consumer has the same level of satisfaction with a different curve. In the latter case we would have what is called an inferior good (one whose substitution effect tends to increase consumption when the price rises). If, on the other hand, the substitution effect were of the same sign as the income effect, we would be dealing with a normal good. But it is the sum of the two effects that would produce the total effect. In the case of normal goods, the income effect will cause their consumption to decrease as the price increases, and this will also happen with inferior goods, except when, in the case of some of the latter, the substitution effect becomes stronger. than that of the income effect, and therefore we would have a Giffen good. When income increases and prices remain constant, normal goods tend to increase in consumption while that of inferior goods decreases.

Note that we have mentioned that when the price rises the consumption of a good will decrease, the analysis is completely symmetrical when the price falls, that is, consumption will increase with the particularities already mentioned in the previous paragraphs. It must also be known that consumption, of course, will also vary with disposable income, increasing or decreasing as it does, until what is called the satiation point is reached for the goods, which would be the maximum possible for the utility function, a point beyond which the consumer would no longer be interested in having more of any of the goods.

Another way goods are related to one another is as complements or substitutes. Complementaries tend to share the same fate when the price of one of them rises or falls, while it is the opposite in the case of substitutes.

It is also possible to consider some goods as evils, the consumption of which produces disutility or negative utility. The evils would be those of which the consumer, unlike the others, would be interested in having as little as possible. For example, in certain microeconomic analyses, wages can be presented as a good and work as a bad and have to study the decision to optimize time taking into account the restriction, that is, more hours of work (bad) produce more wages. (good) and the limit, budget constraint, is the time available for a hypothetical worker.

Demand curve

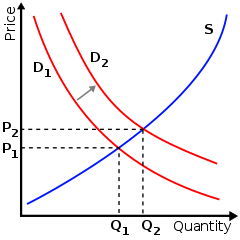
The theory of demand can be derived from the consumer, that is, adding the individual demands of a good and seeing how much the total demand would be for each consumer price. This would lead us to the total demand curve of the good, which is usually represented as a descending curve (negative dependent), because the orderly axis represents the price, and in the abscises the amount of well demanded. It means the lower the price, the higher the demand. The simplified mathematical formula that summarizes this concept, which expresses demand as a straight line is as follows: Qd=a− − bp{displaystyle Q_{d}=a-bp}Where P{displaystyle P} represents the price and a{displaystyle a} and b{displaystyle b} They're constant.

Mathematical representation of the consumer problem

Microeconomics is studied mathematically, using models that avoid the ambiguity of spoken language. Most of the developments and studies of consumer theory are based on the following problem that is represented as follows:

maxU(x1,x2, ,xn){displaystyle max;U(x_{1},x_{2},cdotsx_{n}}}}

s.a:␡ ␡ i=1npixi≤ ≤ M{displaystyle s.a:sum _{i=1}{n}p_{i}x_{i}leq M}

The meaning of this problem is the following: It is about maximizing, that is, obtaining the maximum value of a function, the highest of all that it can give, as well as what values are those that produce that maximum. In this case it would be U{displaystyle U}, which is the utility function of a consumer, which is supposed to depend on the values of the quantities of the n{displaystyle n} goods (represented by variables xn{displaystyle x_{n}} from value 1 to n{displaystyle n}). There is a limit to the values that these variables can take, which is defined by the restriction (s.a{displaystyle s.a} means 'subject to') that as much the total value of the basket of goods can be equal to M{displaystyle M}, that would be the total available rent. This is if we multiply the prices of each good (the pn{displaystyle p_{n}}) for every amount of good, and we add it, and so we get the value of a basket of goods, and that value has to be less or equal (≤ ≤ {displaystyle leq }) M{displaystyle M}, the value of the rent available.

This model is solved using a mathematical technique called the Lagrange Multiplicators (if all available income is supposed to eventually be consumed, which is equivalent to assuming that ␡ ␡ i=1npixi=M{displaystyle sum _{i=1}^{n}p_{i}x) or that of the Karush-Kuhn-Tucker Conditions, if it is believed that it may be on rent (case in which we maintain that the restriction is of the type ≤ ≤ {displaystyle leq }).

The solutions obtained serve us for the previously mentioned analysis, to obtain how the quantities demanded would react if prices changed, and it is possible to study, through modifications to this basic problem, what happens if taxes are introduced on income, indirect taxes, subsidies, what would happen if we consider savings as a good, what happens if we also consider goods whose value is uncertain (as in the case of financial assets), etc., and see how they influence not only the amount of good consumed but also the utility that the consumer receives.

Theory of the producer

In microeconomics, production is simply the conversion of productive factors into products and a company is any organization that is dedicated to the planning, coordination and supervision of production. The company is the decision agent that chooses among the factor-product combinations available to it and maximizes its profit. The problem shares similarities with that of the consumer. In the case of the consumer, microeconomics often reduces it to the question of maximizing a utility function with a budget constraint. In the case of production, it is about maximizing the profit function taking into account technological restrictions (assuming, in principle, that prices are given, a very strong assumption that is subsequently relaxed).

Production function

It begins by considering, for reasons of simplification, that a single good (or service) is produced by a company and that to produce it a series of elements called production factors (they can also be called inputs or inputs) is necessary. The good or service produced is called output. The function that would relate the quantities of the quantity of production factors used with the output obtained is called the production function. The inputs used would be the raw materials, intermediate products (purchased from another company or obtained in another production process of the same company), the human labor used, the supplies of energy, water and the like, the cost of replacing the capital used, machinery, tools), since it suffers wear and tear from use in the manufacturing process. A frequent simplification is to reduce the factors to two: capital and labor. Labor would represent human labor, capital the rest.

Production functions can also have a series of properties that should be highlighted. One of them is that of what are called Economies of scale.

The Profit Maximization Problem

Generally the profit maximization problem can be studied both in the short run and in the long run. In the short term it is considered that one of the inputs, such as capital, has already been decided for the company and the price for it has already been paid. In the long run, however, all the inputs involved may change, for example, if the company varies the amount of capital available. This problem can be represented mathematically as follows:

max(And1,...... ,Andn)한 한 ≈ ≈ P1And1+ +PnAndn− − (C1X1+ +CmXm){displaystyle max _{(Y_{1},dotsY_{n})in Phi }P_{1}Y_{1}+dots +P_{n}Y_{n}Y_{n}-(C_{1}X_{1}+dots +C_{m}X_{m}},with≈ ≈ ={(And1,...... ,Andn)한 한 (R+)n日本語Andi≤ ≤ Fi(xi1,...... xim)!{displaystyleqquad {mbox{con}}Phi ={(Y_{1},dotsY_{n})in (mathbb {R} ^{+}){n}{n}{n}{i}leq F_{i}(x_{i1},dots x_{im}}}}}}}}}}}}

Where the conditions of use of the inputs acquired by the company must also be taken into account. [They can be rewritten for some outputs, see later in (*)]

Xi=␡ ␡ j=1nxi1{displaystyle X_{i}=sum _{j=1}^{n}x

The objective of the company is to maximize its profit, which is the difference between revenue and costs. The total revenues are equal to the outputs produced by the prices at which they are sold (note that we assume that all the company's production is sold, which is not always the case in reality), and the costs are those of multiplying the inputs used by the prices of the outputs. Now, the restrictions would be that the outputs are a function (of production) of the amounts of each of the inputs used, even if an input were not used, it could be considered that the amount of that input used is zero.

(*) If, for example, type 1 input were used in the production of the different possible outputs, the sum of the total used for each of the outputs should be equal to the total of input 1 acquired by the company (That is, if it uses x11 of input 1 to manufacture output 1, x21 to manufacture output 2, etc., then x11+...+xn1=X1, and X1 would be the total of input 1 used). However, and this is important, in some cases it is possible that when using some inputs "they are not consumed" when using them in the manufacture of certain outputs, so it could be that these conditions were not written like that. For example, if we consider the labor time, in hours, of a certain machine as an input, and that machine could produce two or more types of output at the same time, the corresponding restriction would not be introduced in this model, that is, if for For example, the machine would work 8 hours making two different outputs at the same time, it would not distribute the 8 hours between each one of them but would invest the entire time in each one.

This problem can also be solved using the Lagrange Multipliers or the Karush-Kuhn-Tucker conditions.

Cost curves

A common way to simplify the problem is to assume that only one good is produced and that there is only going to be one input that varies according to the output of the firm, all the others being fixed (Note: In a given model, suppose that a set of variables can change while the rest of the variables will remain constant, regardless of their relationships with the rest of the model, it is what is called ceteris paribus, a simplifying technique but one that can lead to error when compared to reality, in which ultimately everything is related to and influences everything) With this, for example, one can study how a company's production of a good will determine the demand for labor by that company.

All the inputs for which the company has already paid, and which will not change in the short term, their total value would give us what is called the Fixed Cost.. On the contrary, the value of the inputs that will change depending on the level of production is decided, will be the Variable Cost.. The sum of the two will be the Total Cost. As the company's production varies, these costs will vary, so-called Cost Curves are obtained for the microeconomic study. The most important would be Variable Cost, Total Cost, Average Cost, and Marginal Cost.

The variable cost curve relates the total variable costs to the level of production. It is generally increasing, but may tend to grow at a slower rate. The Total Cost is practically identical, since it would be a translation of the Variable in the magnitude of the Fixed Cost, which is important especially in Industrial Production Theory because high Fixed costs discourage companies from entering the market.

The average cost curve, on the contrary, can be ascending or descending, even ascending in some sections and descending in others, since this curve informs us of how much, on average, it costs us to produce each output depending on the level of production. For example, it is possible that with a certain production function the value of producing 300 units of output is such that each one costs 1.5 units of money, while producing 600 can each cost us only 1 unit of money. This would possibly be related to the existence of economies of scale, as mentioned before.

The marginal cost curve is of great importance for analysis, which is why certain economic studies are sometimes called "marginalist". This curve, which is mathematically equivalent to the derivative of the Total Cost Curve, represents the more it costs us to produce a unit of output from the previous level of production. For example, if to produce 100 units of a good we have a cost of 1000 monetary units, and to produce 101 units of that same good the cost is 1020 monetary units, the curve would be worth 20 (1020-1000) at the 100 level of production.

The most general analysis to decide the level of production of a company starts from the fact that the company wants to maximize its profit. The benefit is equal to the income (I) minus the costs (C), both are functions dependent on the level of production. From the mathematical point of view, maximizing a function means equaling the derivative of that function to zero with respect to the variable that we want to maximize; If we derive the benefit function, it would be the derivative of its components: income minus costs:

dIdx− − dCdx=0{displaystyle {frac {dI}{dx}}}-{frac {dC}{dx}}=0}

Which leads to the marginal revenue (obtained by the first derivative of the revenue of the company in the profit function) must be equal to the marginal cost, which is the derivative of the Costs of the company, as a condition for the level of production to be the one that maximizes the benefit. If we assume that market prices cannot change due to the performance of the company, but that they are given (because we are in what is called perfect competition, in which there are many companies and none can influence the price), then the condition is: Price must be equal to marginal cost.

One example is: if the company's Benefit function is B(And)=PAnd− − C(And){displaystyle B(Y)=PY-C(Y)} (Price by production is income, to which the total Cost of that production is subtracted), then, if we apply the condition of the first order of maximum of a derivable function (we assume that C{displaystyle C} is a derivable function), we have that condition is P− − C♫(And)=0{displaystyle P-C'(Y)=0}, this is, C♫{displaystyle C'} represents the Marginal Cost of producing the quantity And{displaystyle Y} of output. This is already said to be valid only for a company in perfect competition.

Market structure

The market is made up of four basic elements: consumers, producers, (relative) prices and products. According to the neoclassicalists, the pure market is not (and should not be affected) by foreign agents such as the government or the financial system. In the market of each good or service, different types of situations can occur. These situations are known as market structures, which are grouped as follows:

The perfect competition model

Price and market quantities in the case of a monopolist and the perfect competition.

The perfect competition model describes a market structure that meets the following assumptions:

1. There are no barriers to the entry of new companies and leaving does not imply a cost.
2. There is perfect information about prices, goods and inputs.
3. A homogeneous product, that is, goods are perfect substitutes.
4. There are no externalities, that is, property rights are perfectly defined.
5. Contracts are met because there is an efficient legal apparatus.
6. There are no growing yields in scale or in production or consumption.

If the assumptions are met, we can be sure that the allocation generated by the market is efficient. In fact, in a general equilibrium model, allocations are Pareto efficient.

The market optimality condition requires that price be equal to marginal cost. If the price is lower, some companies exit the market, pushing the price up due to the reduction in the quantity supplied, and if the price is higher, some companies enter the market expecting positive benefits, but in doing so, they push the price down because the offer expands.

The perfect competition model is an ideal entity that tries to capture the essence of economic behavior, both of companies and individuals. Most of the literature deals with analyzing the impact on welfare or efficiency that any of the aforementioned assumptions is not met. Perhaps one of the most important is that of information.

In a competitive market millions of companies (producers) and millions of households (consumers) participate in voluntary trade, seeking to improve their own economic situations. Their actions are coordinated, as by an invisible hand, by a price system, which has an internal logic and works without a central direction.

The main function of the market is to determine the price of goods. The price is generally understood as the value of the good in monetary terms. However, neoclassical models are conceptualized in relative prices, that is, the relationship between different merchandise. The importance of the price mechanism is so great that microeconomic theory is sometimes called “price theory”.

Imperfect competition

Imperfectly competitive markets are those in which producers are large enough to have a noticeable effect on the market price. There are several models of this type of market, including the monopolistic market and the various oligopolistic models.

The fundamental difference with perfectly competitive markets lies in the influence capacity of the supplying companies to control the price. In these markets, the price is not accepted as foreign data, rather the bidders actively intervene in its determination.

In reality, almost all markets are imperfect, with perfect competition being almost a theoretical optimum. On the contrary, in strongly monopolistic markets, competition occurs between capitals, which seek the maximum benefit in competition with investments in other markets. In general, it can be stated that the higher the number of participants, the more competitive the market will be, but monopoly does not imply that there is no competition.

Monopoly

Monopoly (from the Greek, mono=unique and polio=seller) is a market structure characterized by the presence of a single company, which produces a homogeneous good and which behaves non-parametrically in prices, and by the existence of barriers to entry and exit in the market. In general, it has been proven, in the microeconomic models that study it, that when the Monopoly cannot discriminate between its buyers (that is, when it cannot set different prices for each consumer based on his or her possibilities), it instead sets the same price for all possible buyers, in this case, the equilibrium price in the market and the quantity produced of that good, which are determined from where they intersect the Marginal Cost Curve (which depends on the production function of the monopolistic firm) and the Marginal Revenue Curve (which depends on the Demand for the good produced by the firm, demand that depends on the buyers of that good), are such that, generally, they fulfill this:

• The price put by the company is higher than in cases where there is no monopoly.
• The amount produced by the company is also lower than in cases of non-monopoly.
• The total utility perceived by all agents, both the buyers and the monopolistic company, the sum of these profits, is usually lower than in non-monopoly cases.

For all these reasons, and some more, monopolies are viewed negatively in the markets (For example, remember the Anti-Monopoly laws of the U.S.A.). However, there are some unavoidable monopolies, called Natural Monopolies. Sometimes attempts are made to resolve the problems of this type of monopolies in such a way that a public institution (which is supposed to have no interest in maximizing its own benefit, but global well-being) is the one that controls the price and production of that monopoly or that allows you to vary them depending on the users or buyers of the Monopoly.

Oligopoly

In oligopoly (from the Greek oligo=few, polio=seller), it is assumed that there are several companies, but in such a way that none of them can fully impose itself on the market. For this reason, there is a constant struggle between them to be able to take most of the market share in which companies continuously make strategic decisions, taking into account the strengths and weaknesses of the business structure of each one.

The problem can sometimes be posed using game-theoretic methods. For example, given the cost functions of each of the companies involved, each one will dare to offer a certain price, a certain quantity, to the market. But, these offers of the companies, when observed from the point of view of demand, will have an effect on how much quantity is actually demanded for each company, and given the price that each one has set, they will give each one of them a certain profit level. The idea of companies trying to "differentiate" their product with respect to the product of the others, so that they do not seem so "substitutes" and therefore they can be considered as "different" by consumers. Although often these differences in the product are in minimal things such as the presentation of the product, its "quality", the packaging in which it comes, after-sales services, distribution networks, the proximity of the product to the domicile of the consumer, etc. (for this it is necessary to study more the commercial strategies of each company in particular). All this can lead to the study of different types of models.

Generally, when Game Theory is applied, it is assumed that each company can make decisions in its own set of decisions, and that depending on which ones that company and the others take, that company and the others will obtain a certain result. Sometimes this can be represented as each company having a "Reaction Curve" to the actions of the other companies. For example, if the rest of the companies make a series of decisions, and our company in question knows (quite a strong assumption, of course) what decisions the others have made, in order to obtain the maximum benefit it should make certain decisions at its own discretion. time, which depend on those taken by the others.

Hypothetically, if the "reaction curves" of all firms intersect somewhere, that set of decisions for all firms involved would imply "Balance of the Game," because all firms would simultaneously be doing what is best for themselves given what the rest of the companies are doing. This is what is known as a Nash equilibrium. Nash tested under what conditions this Equilibrium can occur. Examples of market equilibria are Cournot's, when firms compete in quantities supplied, and Bertrand's, when they compete in prices.

However, a common case is also that one of the companies is Leader and the rest Followers. In this case, instead of assuming that an equilibrium is going to be reached in which all the companies more or less reach that equilibrium situation simultaneously, the advantage of the Leading company (for example, by having some overwhelming business advantage over the other companies) leads him to first make a decision to which they respond, that is, they are made later by the Follower companies. This is what leads the Leader to take into account, for each decision, that the followers are going to respond in a certain way, so she readjusts her way of deciding taking into account what the decisions of the others will be, as if in In a certain way, he could also control them and put them at the service of his own benefit.

It is also possible that the oligopoly companies agree to act in coordination when offering their goods and setting their prices, thereby achieving greater total benefit for each one of them than when they act separately. The agreement between companies to agree on production or prices is called collusion and the group of companies that have colluded is called a cartel. In these agreements, the price is higher than the marginal cost, being socially inefficient and producing a similar situation, from the point of view of consumers, to that of a monopoly.

Monopolistic competition

Monopolistic competition is a market structure characterized by the presence of many firms that sell heterogeneous products that are close but imperfect substitutes for one another. As these are heterogeneous products, each producer has a certain market power over the good they produce, so monopolistic competition can be defined as an intermediate market structure between monopoly and perfect competition.

The classical model of monopolistic competition was developed by British economist Edward Chamberlin. Chamberlin stated that, due to the heterogeneous nature of the goods and the certain market power that each producer has over them, companies believe they are facing an estimated or "imaginary" demand curve, according to which decisions of the rest of the producers are given. However, for the rest of the competitors it is not optimal to maintain their decisions in the face of a unilateral variation in the production of the i-th company. In this way, there is a real demand curve, which includes the decisions of all producers and which will determine the market equilibrium. In the short run, market equilibrium is reached when the decisions made by firms according to the "imaginary" are compatible with the real demand curve. That is, at the point where both are equal. In the long run, under the assumption of free market entry and exit, there can be no windfall profit, so that equilibrium is reached at the point where the "imaginary" it is tangent to the long-term average cost and coincides with the real market demand. The result is Chamberlin's Excess Capacity Theorem, according to which the company does not reach the efficient level of production in the long run (minimum average cost).

The key to monopolistic competition models is the existence of non-homogeneous products. This is usually explained by the existence of product differentiation, that is, companies produce different varieties of the same good, which gives them a certain market power over it. Product differentiation can be: horizontal, consumers demand goods with different characteristics, or vertical, consumers have a different willingness to pay for the same characteristic. The classic model of horizontal differentiation is that of spatial competition (Hotelling's Law) (1929).

Recent developments

With rational choice theory and other modern approaches, economists increasingly tried to understand social phenomena in which incentives and disincentives existed for people in certain situations. These studies in a way continue the tradition of classical microeconomics.