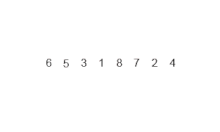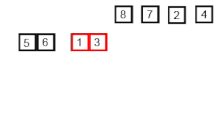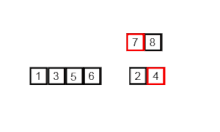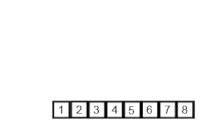Merge Sort

The merge sort algorithm (merge sort) is a stable external sorting algorithm based on the divide-and-conquer technique. It is of complexity O(n log n).

Example of order by mixture.

Description

It was developed in 1945 by John Von Neumann.

Conceptually, merge sort works as follows:

1. If the length of the list is 0 or 1, then it is already ordered. In another case:
2. Split the messy list into two sublists of about half the size.
3. Sort each sublist recursively applying the order by mixture.
4. Mix the two sublists in a single orderly list.

Merge sort incorporates two main ideas to improve its execution time:

1. A small list will need less steps to be ordered than a large list.
2. Less steps are needed to build an orderly list from two also orderly lists, starting from two messy lists. For example, it will only be necessary to link each list once ordered.

The following describes the algorithm in pseudocode (note that special cases for empty vectors etc. are not included; an implementation in a real programming language should take these details into account):

function mergesort(m)
var list left, right, result
if length(m) ≤ 1
return m
else
var middle = length(m) / 2
for each x in m up to middle - 1
add x to left
for each x in m at and after middle
add x to right
left = mergesort(left)
right = mergesort(right)
if last(left) ≤ first(right)
append right to left
return left
result = merge(left, right)
return result

function merge(left, right)
var list result
while length(left)  0 and length(right)
if first(left) ≤ first(right)
append first(left) to result
left = rest(left)
else
append first(right) to result
right = rest(right)
if length(left)  0
append rest(left) to result
if length(right) 
append rest(right) to result
return result

MergeSort sorting It was developed in 1945 by John Von Neumman. The QuickSort method splits the structure in two and sorts each half recursively. The case of mergesort is the opposite, in this method two ordered structures are joined to form a single correctly ordered one. This type of ordering is useful when you have an ordered structure and the new data to be added is stored in a temporary structure and then added to the original structure so that it is ordered again. • Conceptually, merge sort works as follows: • If the length of the list is 0 or 1, then it is already sorted. In another case: • Split the unordered list into two sublists of about half the size. • Sort each sublist recursively by applying merge sort. • Merge the two sublists into a single ordered list. Merge sort incorporates two main ideas to improve its execution time: 1. A small list will need fewer steps to sort than a large list. 2. It takes fewer steps to build an ordered list from two also ordered lists than from two unordered lists. For example, it will only be necessary to interleave each list once they are sorted.

Comparison with other sorting algorithms

Although heapsort has the same time limits as merge sort, it requires only Θ(1) auxiliary space instead of the Θ(n) of merge sort, and is often faster in practical implementations. Quicksort, however, is considered by far to be the fastest general purpose sorting algorithm. On the plus side, merge sort is stable sorting, parallelizes better, and is more efficient at handling slow-access sequential media. Merge sort is often the best option for sorting a linked list: in this situation it is relatively easy to implement merge sort in a way that requires only Θ(1) extra space, and the poor performance of linked lists under random access causes others to algorithms (like quicksort) give poor performance, and for others (like heapsort) it is impossible.

For Perl 5.8, merge sort is the default sorting algorithm (quicksort was in earlier versions of Perl). In Java, Array sorting methods use merge sort or a modification of quicksort depending on the data types and for efficiency reasons switch to insertion sort when sorting less than seven elements in the array.