Mechanical energy
The mechanical energy of a body or physical system is the sum of its kinetic energy and its potential energy. It is a scalar quantity related to the movement of bodies and to forces of mechanical origin, such as gravitational forces and forces of elastic origin, whose main exponent is Hooke's law. Both are conservative forces. The mechanical energy associated with the movement of a body is kinetic energy, which depends on its mass and its speed. On the other hand, the mechanical energy of potential origin or potential energy, has its origin in the conservative forces, comes from the work done by them and depends on its mass and its position. The principle of conservation of energy relates both energies and expresses that the sum of both energies, the potential energy and the kinetic energy of a body or a physical system, remains constant. This sum is known as the mechanical energy of the body or physical system.
However, in real systems, non-conservative forces, such as friction forces, are present and the conservation of mechanical energy is not rigorously verified. However, if the magnitude of the friction forces is negligible in relation to the forces of conservative origin, the mechanical energy of the body changes little and its conservation is applied as a good approximation. When appreciable matter is multiplied, a more general principle of conservation of energy must be applied, which includes work due to frictional forces. In calculating the mechanical energy of a physical system or in applying the principle of conservation of energy, it is crucial to know the type of forces, conservative or non-conservative, to which the physical system is subject, as well as the environment in which they apply.
Introduction
Humans have known how to take advantage of mechanical energy since very early times and in many different applications, starting with the inventions of the Greeks with pulleys and gears or with the Phoenician and Roman war machines. In the case of Roman catapults, the compression work of the catapult arm allows energy to be stored in the machine in the form of potential energy. Most of this energy is then transmitted to the projectile which is fired with energy due to motion, kinetic energy. But part of the energy is also transmitted to the movement of the lever arm and the displacement of the slingshot (both in the form of kinetic energy) and the other part is used in the friction of the strings and in the gears that heat up.
Energy is a scalar magnitude that represents a first integral of the movement and as such, easier to use than the force itself that acts on a mobile. It is a concept that appears in all fields of physics (mechanics, electromagnetism, waves, etc.) and technology, however it is expressed differently in each of them depending on its specific application. The concept of energy in physics is directly related to two other physical quantities, work and heat, which exchange energy with the physical system.
Energy satisfies an important conservation principle so that in any physical process it is conserved. Therefore, the energy balance before carrying out a process is the same as once it is finished (Principle of conservation of energy in its most general sense, including friction forces).
Mechanical energy has two basic contributions, that related to movement and to forces of mechanical origin. The energy associated with the movement of a body is kinetic energy, which depends on its mass and its speed.
In addition to kinetic energy, the other manifestation of mechanical energy is mechanical potential energy related to the nature of the interactions put into play in the physical process that is being developed. In the specific case of Mechanical Energy, it will be gravitational forces or elastic forces. In both cases, the potential energy is a function of the mass of the body involved and its position. A basic example of potential energy is that due to the weight of a body of mass m near the Earth's surface.
The sum of the kinetic and potential energies of an object in a given position in space and at a given instant, is what is defined as the mechanical energy of the material object. In the article these notions are considered as well as the different ways of expressing energy according to the force present or the application that is made, to fluids or solids. Another aspect to consider is the friction between the interacting bodies. In this case, the exchange of energy in the form of heat intervenes, which affects the very formulation of the principle of conservation of energy.
In addition to energy, work or heat, another basic quantity is mechanical power for numerous practical applications in the home and in industry, involving the production and consumption of energy. To use and know the mechanical energy of a body, it is necessary to know the expressions of the kinetic energy in translation and rotation movements as well as the potential energy in the gravitational case or the elastic potential energy of a spring. It goes on to consider the simple expression of gravitational potential energy in the vicinity of the earth's surface.
When dealing with mechanical energy, as explained, it is necessary to take into account its kinetic or potential origin, the type of movement involved, be it rotation or translation, and the main forces that give rise to that mechanical energy. The study would not be complete without considering the role played by mechanical energy when friction forces intervene and the loss of mechanical energy produced by them. On the one hand, with the generation of heat and on the other, generating a change in the structure of the bodies that touch. In such circumstances, the application of the principle of conservation of energy is again considered. For this, it is necessary to introduce the notion of internal energy. To better consider these processes, the notion of conservative forces and non-conservative forces is introduced.
Other physical formulations of mechanical energy and the principle of conservation of energy are, on the one hand, the application to fluids in motion (Bernoulli's Equation). It represents another form of the principle of conservation of energy. And secondly, the role played by the concept of energy in Thermodynamics applied to gases is also briefly included. The first law of thermodynamics relates heat, work, and the change in internal energy of the system to each other. This principle intervenes as a practical case of application of the principle of conservation of energy. In the case of intervening heat and work, there are also limitations on the use of the transformation of heat into work in thermal machines, which is included in the second law of thermodynamics. It is about the First Law of Thermodynamics, which intervenes as a practical case of application of the principle of conservation of energy. Finally, the concepts of mechanical energy are applied in oscillatory movements when there is no friction (simple harmonic movement) and in more real cases with friction (damped movements).
Some devices transform mechanical energy into another type of energy. The large electrical generators at power plants, for example, transform mechanical energy into electrical energy. Electric motors or steam turbines transform electrical energy or heat, respectively, into mechanical energy. And you cannot miss the conversion of wind energy generated by wind turbines into mechanical energy from the propeller and the latter into electrical energy.
Principle of conservation of energy
The conservation of energy is a law that allows a balance to be made of the energy of a physical system when it interacts with its surroundings before and after the interaction. The balance of the energy of the system in all its manifestations, of electrical, gravitational, chemical origin, etc. does not change, remains constant. While it can be converted from one form of energy to another. It constitutes a conservation law or principle that is fulfilled in nature and that imposes restrictions on the evolution of physical systems, just as it happens with other conservation principles of physics.
However, mechanical energy by itself is not always conserved, since some mechanical energy can be transformed into another form of non-mechanical energy. For example, if a block is falling down a ramp and there is friction, the initial mechanical energy of the block will not be equal to the final one, since part of that initial mechanical energy will have been dissipated as heat on the ramp and in the block itself., due to the friction of the block with the ramp. The dissipated energy will be the difference of the initial mechanical energy minus the final mechanical energy of the block. If non-conservative frictional forces are included, the principle of conservation of energy states that the sum of the mechanical energy available to the block before it travels down the ramp is equal to the mechanical energy of the block after its travel plus the energy it loses due to friction. In other words, the principle of conservation of energy in its most general sense includes all the available energy of the system (the block), at a given instant and position, including the energy exchanged by the system outside or with other bodies in the system. around. Energy has different ways of manifesting itself and each of them has a different mathematical expression. In the first place, there is the mechanical energy in its expression of movement or kinetic energy or of potential origin such as gravitational energy due to the gravitational force, or elastic energy due to the forces of elastic origin of fluids and solids, going through other forms of energy such as electrical energy, chemical energy, radiant energy, nuclear energy, mass energy, etc. In turn, energy can be transformed into heat or work and, vice versa, heat and work can increase or decrease the energy of a system.
The notion of energy presents a great interest in practice because it is a first integral of the movement for conservation forces and to satisfy the principle of conservation of energy in its different manifestations, as will be seen throughout the article. To do this it is necessary to know the forms of kinetic and potential energy, the mechanical energy of an object or the internal energy of a system as well as the energy exchanged with its environment. If, for example, it is considered a mobile that ascends and descends on a mountain on the surface of the earth, the principle of conservation of energy expresses that whatever its position on the mountain, in the absence of friction, the sum of kinetic energies Ec=12mv2{displaystyle E_{c}={frac {1}{2}}mv^{2} due to its speed and potential Ep=mgH{displaystyle E_{p}=mgH} due to its height H{displaystyle H}It stays steady. That constant is mechanical energy Emec=Ec+Ep{displaystyle E_{mec}=E_{c}+E_{p}}} on the phone. If the lower position of the mountain is considered the mechanical energy will be all of kinetic origin, Emec=Ecmax=cornstante{displaystyle E_{mec}=E_{cmax}=constant and if it is considered the highest position of the mountain where the potential energy is maximum and the minimum kinetic (if it comes with zero speed) Emec=Epmax=cornstante{displaystyle E_{mec}=E_{pmax}=constant. Any form of energy, in general, is measured in July (J{displaystyle J}) in the International Unity System.
Work
Work is a physical magnitude directly related to the energy of the bodies, has its same dimension and therefore is also measured in July (J{displaystyle J}) in the International System. When forces act upon a body, they perform a job and the two physical quantities involved are, the very displacement carried out by the body and the force that acts on it. Considering conservative forces such as gravitational force or elastic force due to a dock, the work done by these forces on a body increases its kinetic energy Ec{displaystyle E_{c}}or otherwise, it decreases. In both cases, the cause for which Ec{displaystyle E_{c}} the body has varied in a quantity Δ Δ Ec{displaystyle Delta E_{c}}, is due to the work done by forces on material objects. The theorem of kinetic energy specifies the amount of Ec{displaystyle E_{c}} that gains or loses the body under the action of the forces that act upon it.
If a force F→ → {displaystyle {vec {F}}} is applied on a particle that describes a curviline trajectory and dr→ → {displaystyle {vec {dr}}} is an elementary shift on the curve, the work done by force to move the particle from position P1{displaystyle P_{1}} until P2{displaystyle P_{2}}It is
W=∫ ∫ P1P2F→ → ⋅ ⋅ dr→ → {displaystyle W=int _{P1}{P2}{vec {F}}{cdot {vec {dr}}}}}{cdot {vec {dr}}}}}}} which can also be expressed as, W=∫ ∫ P1P2Fsds=∫ ∫ P1P2F# θ θ ds{displaystyle W=int _{P1}{P2}F_{s};ds=int _{P1}{P2}F;cos {theta };ds}
being P1{displaystyle P1} and P2{displaystyle P2} the starting and end points of the path, Fs{displaystyle F_{s}} the projection of the force on the tangent direction to the curve, F{displaystyle F} the force module, ds{displaystyle ds} the length of elementary displacement (ds=日本語dr→ → 日本語){displaystyle (ds=associated{vec {dr}} and θ θ {displaystyle theta } the angle formed by force and tangent to the trajectory at each point.
In simpler cases such as a constant force applied to the mobile and in the same direction and sense of movement F→ → =F⋅ ⋅ i→ → {displaystyle {vec {F}}=Fcdot {vec {i}}}This one will travel a distance s→ → =s⋅ ⋅ i→ → {displaystyle {vec {s}}=scdot {vec {i}}} describing a rectilinear trajectory. The force will do a job (W{displaystyle W}) on the particle given by
W=F→ → ⋅ ⋅ s→ → =Fs{displaystyle W={vec {F}}cdot {vec {s}}=Fs}(singing) # θ θ =1{displaystyle cos {theta }=1;} in this case).
Power
Power is defined (P{displaystyle P}) as the speed with which the work is done. Average power (Pmed{displaystyle P_{med}}) is the work (Δ Δ W{displaystyle Delta W}) performed for a time (Δ Δ W{displaystyle Delta W}) divided by the value of such time(Δ Δ t{displaystyle Delta t}).
Pmed=Δ Δ WΔ Δ t{displaystyle P_{med}={frac {Delta W}{Delta t}}}}
Instantaneous power is defined as:
P=F→ → ⋅ ⋅ v→ → {displaystyle P={vec {F}}cdot {vec {v}}}
being F→ → {displaystyle {vec {F}}} the force that acts on the particle and v→ → {displaystyle {vec {v}}} Instant particle speed.
The power has power units in the time unit and is measured in watts (W{displaystyle W}) in the International System (IS).
Kinetic energy
Kinetic Energy Theorem
For any net force acting on a mass particle m{displaystyle m} that moves along any curviline trajectory, you can prove that your work is equal to the variation of the kinetic energy of the particle.
W=∫ ∫ P1P2F→ → ⋅ ⋅ dr→ → =∫ ∫ t1t2F→ → ⋅ ⋅ v→ → dt=m∫ ∫ t1t2a→ → ⋅ ⋅ v→ → dt=m2∫ ∫ t1t2d(v2)dtdt=m2∫ ∫ v12v22d(v2)=mv222− − mv122=Δ Δ Ec=Ec2− − Ec1{cHFFFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFF}{cHFF}{cHFF}{cHFFFF}}{cHFF}{cHFF}{cHFFFFFFFF}{cHFF}{cHFF}{cHFF}{cHFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFF}{cHFF}{cH}{cHFFFF}{cHFF}{cHFFFFFF}{cHFF}{cHFF}{cHFFFFFF}{cHFF}{cHFFFF}{cHFF}{cHFFFF}{cH}{cHFF}{cHFF}{cH}{c
being,
a→ → {displaystyle ;{vec {a}};} the vector particle acceleration, F→ → =m⋅ ⋅ a→ → {displaystyle ;{vec {F}}=mcdot {vec {a};} the Second Law of Newton applied to the mass particle m{displaystyle m}, v→ → {displaystyle ;{vec {v}};} your vector speed, dr→ → =v→ → dt{displaystyle ;{overrightarrow {dr}}={vec {v}},dt;} the vector elemental movement of the mobile over the curve t1{displaystyle ;t_{1},} and t2{displaystyle t_{2},} initial and final moments associated with positions P1{displaystyle P_{1},} and P2{displaystyle P_{2},} initial and end of the trajectory, respectively.
This relationship expresses that: the work performed by a F force on a particle along a curve from an initial moment to a final one, is equal to the variation of kinetic energy of the mobile between both moments of time, is the Theorem of variation of kinetic energy. It is always verified, regardless of the nature of force F{displaystyle F} which can be conservative, non-conservative or can be the result of forces of different nature.
- NOTE: justification of the intermediate steps for the demonstration of kinetic energy theorem
d(v2)dt=d(v→ → .v→ → )dt=dv→ → dt.v→ → +v→ → .dv→ → dt=2dv→ → dt.v→ → =2a→ → .v→ → {cHFFFFFF}{cHFFFFFF}{cHFFFFFF}}{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFFFF}{c}{cHFFFFFFFFFFFFFFFF}{cH00}{c}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}}{cH00}{c}{cH00}{cHFFFFFFFFFFFF00}{c}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Kinetic energy
Kinetic energy is presented with different expressions depending on the type of movement described and the nature of the material medium.
Translation
According to the theorem of kinetic energy, kinetic energy of a mass block m{displaystyle m} that moves through a horizontal surface with a speed v{displaystyle v} is the work done by force to carry the block from the rest (v=0){displaystyle (v=0)} up to speed v{displaystyle v} determined. This body has won a mechanical energy equal to the kinetic energy reached at speed v{displaystyle v}, as a result of the work performed by the force that is applied until reaching the aforementioned speed.
Ec=12mv2{displaystyle E_{c}={frac {1}{2}}mv^{2}
Another interpretation that can be given to kinetic energy is that of the work that performs a force on a motion particle, with a certain initial speed, opposing it, until stopping it. The kinetic energy is a scale, therefore without direction or sense, as is all kinds of energy, and is always greater or equal to 0 (J){displaystyle (J)}. On this occasion, the particle has lost all its initial mechanical energy.
To analyze this type of energy in motion we can consider a pendulum. If the mass of the pendulum is released from one end so that it swings from one side to the other, it loses height in its movement until it reaches the lowest point. The potential energy is minimal in this place, despite which, the mass does not stop and continues its movement. This is thanks to a different energy, independent of its trajectory and the mechanism that originates it, which allows it to rise again, the kinetic energy. In turn, when reaching the maximum height, this other form of energy disappears, the potential energy reaches a maximum and the process is repeated.
In order to obtain a formula that expresses the energy associated with the movement, it is necessary to take into account that at the lower point there must be a quantity of energy that allows it to rise again to a certain height. As this energy is associated with the movement receives the name of kinetic energy. The kinetic energy reached at the lowest point is equivalent to its maximum potential energy, that is, to the weight P=mg{displaystyle P=mg} multiplied by height h{displaystyle h} which can reach the pendulum in correspondence with its speed: Ec=Ph{displaystyle E_{c}=ph}. If this formula is expressed according to the variables v{displaystyle v}, speed of movement, and g{displaystyle g}, motion acceleration, you get: Ec=12gPv2{displaystyle E_{c}={{frac {1}{2g}}}Pv^{2}}}}, since h=v22g{displaystyle h={frac {v^{2}}{2g}}}}}. This is because the mechanical energy of the pendulum is preserved and all the potential energy it stores, at a maximum height h{displaystyle h}, transforms into maximum kinetic energy, due to movement with speed v{displaystyle v} in its lower part.
The fact that the movement is associated with energy has nothing to do with the fact that the pendulum is in a gravitational field. The previously derived formula for kinetic energy is incorrect for high speeds due to the need for a relativistic correction.
Rotation
It will deduce the expression of the kinetic energy of a solid body that revolves around an axis with a angular velocity ω ω {displaystyle omega } and is subject to a couple of forces at the moment Δ Δ {displaystyle tau }. Instead of the notion of mass m the moment of inertia must be used I{displaystyle I} of the solid with respect to the axis of rotation, instead of distances we must employ angles θ θ {displaystyle theta } and instead of linear accelerations a{displaystyle a} angular accelerations must be used α α {displaystyle alpha }.
Work W{displaystyle W} produced by the pair of forces Δ Δ {displaystyle tau } when making a angular shift θ θ 1{displaystyle theta _{1}} a θ θ 2{displaystyle theta _{2}} expressed by the integral θ θ 1{displaystyle theta _{1}} and θ θ 2{displaystyle theta _{2}} of elementary work Δ Δ {displaystyle tau } δ δ θ θ {displaystyle delta theta }:
W=∫ ∫ θ θ 1θ θ 2Δ Δ ⋅ ⋅ δ δ θ θ {displaystyle W=int _{theta _{1}}{theta _{2}{2}tau cdot delta theta }
If the pair of forces Δ Δ {displaystyle tau } was constant and the finite described angle Δ Δ θ θ =θ θ 2− − θ θ 1{displaystyle Delta theta =theta _{2}-theta _{1} the general expression would be reduced to the product of the pair (θ θ {displaystyle theta }) for angular displacement (θ θ 2− − θ θ 1){displaystyle (theta _{2}-theta _{1})}:
W=Δ Δ ⋅ ⋅ Δ Δ θ θ {displaystyle W=tau cdot Delta theta }
In a general case of rotation dynamics where Newton's law is replaced by Δ Δ =Iα α {displaystyle tau = Ialpha } the elementary work performed would be
Δ Δ dθ θ =Iα α dθ θ =Idω ω dtdθ θ =Iω ω dω ω =I12d(ω ω 2){displaystyle tau dtheta =Ialpha dtheta =I{frac {domega }{dt}}dtheta =Iomega domega =I{frac {1}{2}}d(omega ^{2})}} and the variation of the corresponding kinetic energy would be represented by the expression:
W=∫ ∫ ω ω 1ω ω 2I12d(ω ω 2)=(12I(ω ω 2)2− − 12I(ω ω 1)2)=Ec2− − Ec1{displaystyle W=int _{omega _{1}}{omega _{2}{2}I{frac {1}{2}}{2}}{2})=({frac}{2}{2}}{2}}{2}}{2}{2}{2}{2}{2}{1}{1}{1}{1}{1}{2}{1}}}{1}}}{1}{1}{1}}{1}}{1}{
Where ω ω 1{displaystyle omega _{1}} and ω ω 2{displaystyle omega _{2}} represent the values of angular speed and α α 1{displaystyle alpha _{1}} and α α 2{displaystyle alpha _{2}} those of the angular acceleration of the solid in situations 1 and 2, respectively. This is the Theorem of kinetic Energy for a work done by a couple of forces in a angular displacement. The expression of the kinetic energy of rotation, therefore, is
Ec=12Iω ω 2{displaystyle E_{c}={frac {1}{2}}Iomega ^{2}}.
An example of interest is the conical pendulum of length l{displaystyle l}, which acts as a speed selector, to a greater pair of forces exerted on the pendulum, greater speed will reach, greater will be its kinetic energy of rotation and greater, therefore will be the height reached. This is because the angle φ φ {displaystyle phi } which forms with vertical increases by increasing angular speed, according to law corsφ φ =gl.ω ω 2{displaystyle cosphi ={frac {g}{l.omega ^{2}}}}}}
Instant power developed in the rotation movement, if the pair Δ Δ {displaystyle tau } is constant, expressed by:
P=dWdt=Δ Δ ⋅ ⋅ ω ω {displaystyle P={frac {dW}{dt}}=tau cdot omega }
Potential energy
Gravitational Potential Energy
The gravitational force (attractive) that the Earth exerts on a mass body m{displaystyle m} is given by the expression:
Fg=GmTmr2{displaystyle F_{g}=G{frac {m_{T}m}{r^{2}}}}}}}}{
where mT{displaystyle m_{T}} is the mass of the Earth, r{displaystyle r} the distance from the body to the center of the Earth and G is the constant universal gravitation which has a value approximately equal to 6,6742 × 10−11 N.m2/kg2.
The expression of the work performed by the gravitational force by moving the body from the height r1{displaystyle r_{1}} up to the height r2{displaystyle r_{2}} will be the following:
Wgrav=∫ ∫ r1r2Fr⋅ ⋅ dl{displaystyle W_{grav}=int _{r_{1}}}^{r_{2}F_{r}cdot dl}
Where Fr{displaystyle F_{r}} is the radial component (taken according to the vertical) of the gravitational force Fg{displaystyle F_{g}} and dl{displaystyle dl} a small variation of height.
Replace the component Fr{displaystyle F_{r}} in the expression of work W{displaystyle W}, is obtained for the work of gravitational force:
Wgrav=− − GmTm∫ ∫ r1r2drr2=GmTmr2− − GmTmr1=U2− − U1{displaystyle W_{grav}=-Gm_{T}mint _{r_{1}{r_{r_{2}}}{frac {dr}{r^{2}}}}}}=G{frac}{m}{r_{2}{2}}}}{r-G{frac {m}{r_{1}{1}{1}{1}}}}}{1}}}{1}}}}{r}}{1⁄2}}}}}}{r}}}}}}{1⁄2}}}}}}}}}}}{r}}{r
Where U=− − GmTmr{displaystyle U=-G{frac {m_{T}m}{r}}}} is the expression of potential gravitational energy. Note that the potential energy is nullified in infinity (at very large distances) and grows in module as it approaches the center of the Earth. In other words, the value of potential energy is being measured with respect to a very distant point where the origin of potential energies is considered.
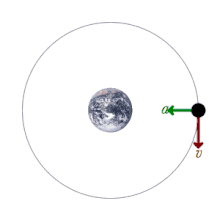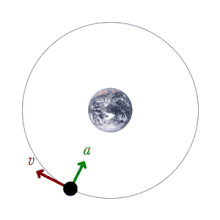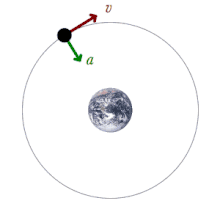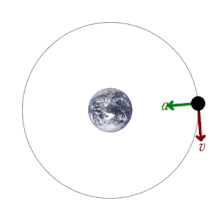
In the event that the orbit described was circular, which can be quite close to reality, the speed of the satellite would be constant and the movement described circular uniform. Calling v{displaystyle v} at speed, T{displaystyle T} the period used by the satellite in orbit and r{displaystyle r} the height of the same measured relative to the center of the earth can be applied the second law of Newton, the force that acts is the gravitational, the mass of the satellite is m{displaystyle m} and acceleration is centrifugal acceleration a=v2r{displaystyle a={frac {v^{2}}{r}}}}}. Therefore the dynamic balance situation requires: GmTmr=mv2r{displaystyle G{frac {m_{T}m}{r}}}}={frac {mv^{2}{r}}}}}}Wherever it clears v{displaystyle v} obtained v=GmTr{displaystyle v={sqrt {G{frac {m_{T}}{r}}}}}}}.
From this it can be deduced that the speed of the satellite does not depend on its mass, but solely and exclusively on the mass of the Earth and the height measured with respect to its center.
Second, the period T{displaystyle T} which takes the satellite to describe a complete orbit is obtained from the following expression:
v=2π π rT{displaystyle v={frac {2pi r}{T}}}
for this reason, clearing the T and substituting the expression of the v, we obtain:
T=2π π rrGmT=2π π r3/2GmT{displaystyle T=2pi r{sqrt {frac {r}{Gm_{T}}}}}}{frac {2pi r^{3/2}{sqrt {Gm_{T}}}}}}}}}}It can be observed that the larger the orbit, the lower the speed and the greater the satellite period.
Gravitational potential energy in the vicinity of the earth's surface

The expression of the potential gravitational energy in the vicinity of the earth's surface acquires a simple and very practical way. However, infinity is not taken as the source of potential energy, as has been done in the previous paragraph, but it is much more practical to take the Earth's surface as a potential source of energy (potential zero energy). The expression of this energy will be deduced. To do so, the position of the mass body m{displaystyle m} measured by height h{displaystyle h} which has measurement with respect to the soil and taken according to the vertical. The condition of closeness of the body to the earth surface is expressed mathematically by condition <math alttext="{displaystyle h<h;RT{displaystyle h vis within<img alt="{displaystyle h<Where RT{displaystyle R_{T}} represents the terrestrial radio.
Ep(h)=(− − GmTmRT+h)− − (− − GmTmRT)=mGmTRT2h=mgh{displaystyle E_{p}(h)=(-G{frac {m_{Tm}{R_{R}}{T+h}}})-(-G{frac {m_{T}m}{R_{T}}}}})=m{frac {Gm_{T}}}{R_{T}{2}{
where g=GmTRT2{displaystyle g={frac {Gm_{T}}{R_{T}^{2}}}}}}is a constant (obtained from three other constants) that has acceleration dimensions and is the acceleration of gravity on the surface of the earth.
Ep(h)=mgh{displaystyle E_{p}(h)=mgh} is the well-known expression of potential energy Ep(h){displaystyle E_{p}(h)} due to weight P=mg{displaystyle P=mg} of a mass m{displaystyle m} near the surface of the Earth at a height h{displaystyle h} above your lower position.
An intuitive way to know the potential energy due to the weight of a body is due to the mathematician Simon Stevin. In his epitaph he appears a chain in balance on a tilted plane. The number of balls that remain in the vertical part of the plane provides an idea of the potential energy of the balls on the tilted plane. If the plane had more slope, greater would be in number of balls in the vertical and greater part would be the potential energy of the balls on the tilted plane. And vice versa, if the height is diminishing, less will be the number of balls in the vertical and lower their potential energy to reach the height h=0{displaystyle h=0} where in the vertical there is no ball and correspondingly the potential energy of the chain would be zero.
Elastic Potential Energy
As already mentioned in the introduction, the simplest system to analyze the behavior of elastic forces is the spring applied to a block of small dimensions and mass m. To keep a stretched spring in a length x{displaystyle x} beyond its natural or equilibrium length, one must apply a force whose module can be expressed as: 日本語Fx日本語=k日本語x日本語{displaystyle 日本語F_{x}{x}Where k{displaystyle k} is the elastic constant of the spring that is measured in N/m in the SI. When the spring is stretched or compressed, with a fixed end and the other is subject to the mass, a recovering force appears Fx{displaystyle F_{x}} on this dough subject to the dock equal and otherwise sense, so Fx=− − kx{displaystyle F_{x}=-kx} and this force always tends to lead the mass to the position of balance, where the dock is in its natural length (both if it has been stretched as if it has been contracted). This expression establishes a linear relationship between elastic force and distance x{displaystyle x} that the dock has been compressed or stretched, and is known as the law of Hooke.
If you want to calculate the work of the elastic force done on the dough attached to the dock at the free end, just stretch the dough a distance x{displaystyle x} and observe the shift to the balance position x=0{displaystyle x=0}produced by elastic force Fx{displaystyle F_{x}}. The work done by the elastic force is stored in the spring in the form of potential elastic energy Ep{displaystyle E_{p}}. You can calculate this work of elastic force acting on the mass more intuitively as the area under the straight Fx=kx{displaystyle F_{x}=kx}with the linear relationship between the elastic force Fx{displaystyle F_{x}} and variable x{displaystyle x}, which represents the stretched or compressed amount of the dock. As the spring's recovery force is conservative, you can relate this work to the potential energy available for the mass, depending on the distance x{displaystyle x} and the energy stored at the dock.
To calculate this work, it is of interest to resort to the graphic representation of linear law Fx=kx{displaystyle F_{x}=kx} and calculate the work W{displaystyle W} performed against the elastic force to transfer the mass subject to the dock, stretching it from the balance position x=0{displaystyle x=0} to a position 0}" xmlns="http://www.w3.org/1998/Math/MathML">x▪0{displaystyle x 2005}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>. Therefore, if an elongation is represented in a figure x{displaystyle x} in the horizontal axis and strength Fx{displaystyle F_{x}} in the vertical axis, Hooke's law is described by a slope line k{displaystyle k}.
The work done against the elastic force to transfer the mass m from the resting position (x=0){displaystyle (x=0)} until position x{displaystyle x} It will be: W=∫ ∫ 0xFxdx=∫ ∫ 0xkxdx=12kx2{displaystyle W=int _{0}^{x}F_{x},dx=int _{0}^{x}kx,dx={1over 2}kx^{2}}}, which graphically corresponds to the area of triangle understood between 0{displaystyle} and x{displaystyle x}. As discussed, the elastic force is conservative and its work represents the variation of a potential energy that stores the dock according to elongation x{displaystyle x} and from which the m mass is available in its oscillatory movement. This elastic potential energy that acquires the dough subject to the dock, when it is in position x{displaystyle x}It's: Ep=12kx2{displaystyle E_{p}={1over 2}kx^{2}}}
The work done on mass m, against elastic force, in a stretch of x1{displaystyle x_{1}} a x2{displaystyle x_{2}} will be given by the expression:
W=∫ ∫ x1x2Fxdx=∫ ∫ x1x2kxdx=12k(x22− − x12)=Ep2− − Ep1{displaystyle W=int _{x_{1}}^{x_{2}}}F_{x},dx=int _{x_{1}}}{xx_{2}}}}kx,dx={1 over 2}k(x_{2}{2}{2}-x_{1}{2}}{2})=What represents the increase of potential elastic energy that acquires mass m by stretching the dock x1{displaystyle x_{1}} a x2{displaystyle x_{2}}. If the spring is compressed over its natural length, instead of stretching, the reasoning is analogous but elongation x{displaystyle x} of the dock regarding its balance position will be negative. In this way the m mass will oscillate around the position of balance x=0{displaystyle x=0} between a maximum stretch position xmax{displaystyle x_{max}} and another maximum compression − − xmax{displaystyle -x_{max}}. The potential elastic energy will be maximum in the extreme positions of elongation and compression and will be zero in balance.
If on the body that acts the elastic force also acts the gravitational force, for having a mass m{displaystyle m}, as both are conservative have a potential energy associated. The total potential energy that the body then acquires, by virtue of its position, will be the sum of the gravitational and elastic potential energies: Ep=Ep(elast.)+Ep(grav.){displaystyle E_{p}=E_{p(elast)}+E_{p(grav.)}}.
Other forms of energy
We have just considered how the energy due to the elastic force that manifests itself when the spring is under tension or under compression. If a small block attached to a compressed spring is placed in a horizontal position (so that the effect of gravity does not affect the system) and is released, its oscillatory movement can be observed as the spring is alternately stretched and compressed, each time passing through the equilibrium position. Due to air resistance, the block after a certain time comes to a stop. It happens then that all the potential energy of which the block was available at the beginning in the form of elastic potential energy ends up dissipating abroad in the form of heat. Heat is, therefore, another form of energy originated by the movement of the particles that make up the internal structure of the solid material from which the spring is made. This new manifestation of energy represents the thermal agitation of the surrounding air molecules that causes the temperature of the environment to increase.
There are many other forms of energy of which a brief description will be made. Electrical energy that is related to the movement of electrical charges; Radiant energy, which is the electromagnetic energy carried by waves of the electromagnetic spectrum, of special interest when they are in the region of the visible spectrum. Mention of interest also chemical energy that is released in chemical reactions, and nuclear energy whose forces govern the laws of particles within the nucleus.
When considered particles with very high speeds (near to speed of light in vacuum), according to the theory of relativity, it is necessary to modify the expressions of the kinetic energy of such particles. Considering a mass particle m{displaystyle m}as in the relativistic expression the mass depends on the speed m(v){displaystyle m(v)}His mass of rest m0{displaystyle m_{0}} already has an energy m0c2{displaystyle m_{0}c^{2}}Where c{displaystyle c} is the speed of light in the vacuum and the total energy of the particle is E=mc2{displaystyle E=mc^{2}}. In addition the kinetic energy of the relativist particle can be calculated based on its total energy and its resting energy: Ec=mc2− − m0c2{displaystyle E_{c}=mc^{2}-m_{0}c^{2}. If the velocity of the particle is much lower than that of light the previous expression is reduced to the already known Ec=12mv2{displaystyle E_{c}={frac {1}{2}}mv^{2}. The expression of relativistic energy E=mc2{displaystyle E=mc^{2}} It gives an important meaning, when analyzing the principle of energy conservation, since it takes into account the energy that a body possesses as a result of its mass. When it is attached to this principle in its most general expression, the mass-energy equivalence of Special Relativity is implied. There are many forms of energy and energy due to the mass can be considered as one of them. As an example, there is an example of energy conservation that takes into account energy associated with the mass of particles. If in a PET team they collid a positron and an electron, both with the same resting mass, as a result of their annihilation give rise to a certain amount of radiant energy equivalent, which can be measured and calculated in the experience. To do this, it is enough to know, at the time of the collision, the mass of the two particles that annihilate each other, thus releasing the energy due to the mass they contain: E=mec2+mpc2{displaystyle E=m_{e}c^{2}+m_{p}c^{2}
Loss of mechanical energy
Heat
Heat is a form of energy transfer between a system and its surrounding medium. When analyzing the microscopic origin of this energy transfer, we observe that when the molecules that make up the system receive heat from outside, there is an increase in their average kinetic energy, that is, an increase in their thermal agitation kinetic energy. and vice versa, a decrease in its average kinetic energy means a transfer of energy in the form of heat to the outside. However, the energy stored in a system is not heat, nor is work, both physical magnitudes represent energy in transit that is absorbed or released by bodies. In addition, the heat is usually dissipated in the surroundings of the system, which means a loss of energy by the bodies involved in the process. In 1845, James Prescott Joule published a paper 'The Mechanical Equivalent of Heat', in which he derives a concrete numerical value for the amount of mechanical work needed to produce one unit of heat, it is the mechanical equivalent of heat that allows expressing the unit of heat, the calorie, in joules.
The SI unit of heat is the joule (J), although it can also be expressed in calories (the traditional unit for heat):
1 (calorie) = 4.1840 (joules)
Heat is a form of energy exchange in physical systems when they are subjected to a series of processes in which they absorb or release energy. A system to absorb heat and increase its internal energy, increases its temperature. The notion of temperature is related to the state of thermal agitation of the particles that make up the system. Therefore, when there is no exchange of energy with the outside, it is said that the system is in thermal equilibrium and the objects that make up the system will all have the same temperature and equal to that of the surroundings.
For there to be thermal equilibrium between two systems, the average kinetic energies of the particles of the interacting systems have to be the same. This is because the average kinetic energy of the system is a measure of its state of thermal agitation.
Defining the average kinetic energy (by particle) for a system N{displaystyle N} particles each of them of mass mi(i=1,2,3,...N){displaystyle m_{i};(i=1,2,3,...n)} like:
Ec=1N(・ ・ i12mivi2){displaystyle E_{c}={frac {1}{n}}}(sigma _{i}{frac {1}{2}{2}}m_{i}v_{i}{2}}}{2}}}}}
-N{displaystyle N} is the total number of particles
-vi{displaystyle v_{i}} is the speed of the i-sima particle of the system
Applied to a gas containing N molecules, the approximate form of its kinetic energy is: Ec=12Nmv2! ! {displaystyle E_{c}={frac {1}{2}}Nm{overline {v^{2}}}}, being mv2! ! {displaystyle m{overline {v^{2}}}}} the average quadratic velocity of the gas molecules. In addition, the kinetic theory of gases states that the average quadratic velocity of molecules can be expressed as: v2! ! =3kBTm{displaystyle {overline {v^{2}}}{3k_{B}T over m}}, being kB{displaystyle k_{B}} Boltzmann's constant and m{displaystyle m} molecular mass. So the absolute temperature of the gas T{displaystyle displaystyle T} can be expressed based on kinetic energy Ec{displaystyle E_{c}} of the system as:
T=mv2! ! 3kB{displaystyle displaystyle T={m{overline {v^{2}}} over 3k_{B}}}}}
and therefore the temperature,
T=23EcNkB{displaystyle displaystyle T={frac {2}{3}}{frac {E_{c}}{Nk_{B}}}}}}{Nk,
This is an important result of kinetic theory: "the average kinetic energy of molecules is proportional to the absolute temperature of the ideal gas".
Thus the temperature appears as a quantity related to the average kinetic energy of the particles of the system. It can be stated that: two systems in thermal equilibrium must be at the same temperature, and that energy can be exchanged in the form of heat only when the temperature of two systems is different, heat being transferred naturally from the higher to the lower temperature body (direction of the arrow of an irreversible process). The direction of the arrow (the only direction in which the process is carried out) in natural processes is regulated by the second principle of Thermodynamics through the entropy function. The entropy function of the system added to that of the surroundings that interact with it always increases when an irreversible process takes place.
Work of non-conservative forces
The work done by the dissipative, friction or non-conservative forces is manifested as a loss of mechanical energy Δ Δ Emec{displaystyle Delta E_{mec}}. It has its origin in the forces of friction between solids, which provide the W mechanical work that finally gives the loss of energy, when the body is moving on a unpolished surface and its mechanical energy is measured at the beginning and end of the route: Efinal− − Einicial=Δ Δ Emec{displaystyle E_{final}-E_{inicial}= and Δ Δ Emec=Wnorcornservativas{displaystyle Delta E_{mec}=W_{no conservative}}}. This type of force does not derive from potential energy unlike conservative forces such as gravity or elastic force. While dissipative forces have empirical laws whose effects are manifested in deformations of the solids and in losses of mechanical energy, they originate, at the molecular level of matter, in the electromagnetic forces. Thus, the loss of mechanical energy is exchanged with the outside in the form of heat. If we consider all available energy including heat loss by the body subject to dissipative forces, it must be the same as the initial mechanical energy. In this sense we speak of a principle of conservation of the most general energy: The total energy of an isolated system remains constant, that Albert Einstein generalized in his principle of equivalence of mass-energy
Frictional forces
Work of the friction force
The force of friction is a force that opposes the movement. If considered a force F{displaystyle F} constant, work W{displaystyle W} performed the force on an object, produces a displacement 0}" xmlns="http://www.w3.org/1998/Math/MathML">Δ Δ x▪0{displaystyle Delta x 20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80ff8f6a17e8b6069576699d4e44ebdc920a581e" style="vertical-align: -0.338ex; width:7.526ex; height:2.176ex;"/> positive
W=F→ → .Δ Δ x→ → =FΔ Δ xcorsθ θ {displaystyle W={vec {F}}.,{overrightarrow {Delta x}}}=FDelta x,costheta }
Yeah. F{displaystyle F} is a force of friction will have an opposite sign to the displacement and therefore at angle between the force and the displacement vector θ θ =π π {displaystyle theta =pi } and therefore work W{displaystyle W} realized will also be negative.
<math alttext="{displaystyle W=-F,Delta xW=− − FΔ Δ x.0{displaystyle W=-F,Delta x vis0}<img alt="{displaystyle W=-F,Delta x
Friction between solids
Law of conservation of energy when friction forces appear
Due to the friction between solids, there is a heat dissipation to the outside of them. This is due to the roughness of the common surfaces of separation that causes a change in the mechanical energy of the solids subject to friction forces, freeing it in the form of heat and also deforming the bodies. If the internal structure of the two bodies whose surfaces are subject to friction is considered, there may be a change in their structure as a result of dynamic friction. In that case, the energy associated with changing its structure or changing the temperature of the two bodies causes a change or variation in the internal energy of the material or materials involved that will not be considered. The bodies subject to friction heat up their temperature until they reach a balance temperature. Once they reach their balance temperature, the loss of energy in the form of heat to the outside of the bodies begins. What must always be taken into account, therefore, is the dissipation of energy, in the form of heat to the outside, as a result of the work of the friction forces. In the case of mass block m{displaystyle m} sliding down the rough surface, this work is equal to the reduction of the kinetic energy of the block that by slowing down its speed ends up standing. With the help of the theorem of kinetic energy, TEC, you can verify this reasoning. If the mechanical power variation of the block is calculated by sliding on a horizontal surface not polished from position 1 with a speed v1{displaystyle v_{1}} up to position 2 with speed v2{displaystyle v_{2}}, applying the TEC, you get:
Δ Δ Emec=Emec1− − Emec2=Δ Δ Ec=12mv22− − 12mv12=Wdis{displaystyle Delta E_{mec}=E_{mec_{1}}}-E_{mec_{2}=Delta E_{c}={1 over 2}mv_{2}{2}-{2}-{1 over 2}mv_{1}{2}=
The calculation of the work of the disipative force Wdis{displaystyle W_{display} is obtained by expressing the force of friction of the block with the surface as
Fdis=− − μ μ N{displaystyle F_{dis}=-mu N}, being μ μ {displaystyle mu } the coefficient of friction between both surfaces and N{displaystyle N} the normal pressure force between the two, allows to obtain
Wdis=− − μ μ NΔ Δ x{displaystyle W_{dis}=-mu NDelta x}, negative for always being the sense of displacement opposite to the force of friction. Thus, the TEC is expressed: <math alttext="{displaystyle Delta E_{mec}=Delta E_{c}={1 over 2}mv_{2}^{2}-{1 over 2}mv_{1}^{2}=-mu NDelta xΔ Δ Emec=Δ Δ Ec=12mv22− − 12mv12=− − μ μ NΔ Δ x.0{displaystyle Delta E_{mec}=Delta E_{c}={1 over 2}mv_{2}^{2}-{1 over 2}mv_{1⁄2}{2}=-mu NDelta x Â0}<img alt="{displaystyle Delta E_{mec}=Delta E_{c}={1 over 2}mv_{2}^{2}-{1 over 2}mv_{1}^{2}=-mu NDelta x,
for what <math alttext="{displaystyle v_{2}v2.v1{displaystyle v_{2}{1}{1}}<img alt="{displaystyle v_{2} and <math alttext="{displaystyle E_{mec_{2}}Emec2.Emec1{displaystyle E_{mec_{2}}}{mec_{1}}}}<img alt="{displaystyle E_{mec_{2}}as justified.
Therefore it can be said that the decrease (negative sign) in mechanical energy is equal to the work performed by the friction or friction forces. To analyze the difference between the work performed by a dissipative force and a preservative is shown, then the result of the work done in a cycle, in two different examples, one by the force of friction and another by the conservative force of the weight. When you want to calculate the total work of the friction force Wdis{displaystyle W_{display}, back and forth, as the body moves through a rough surface a distance d{displaystyle d}, this total work is negative and in absolute value is twice that of one. In fact, if the force of breaking the block with the surface is: Fdis=− − μ μ N{displaystyle F_{dis}=-mu N}, being μ μ {displaystyle mu } the coefficient of friction between both surfaces and N{displaystyle N} the normal pressure force between the two,<math alttext="{displaystyle W_{dis}(total)=W_{dis}(ida)+W_{dis}(vuelta)=-mu Nd-mu Nd=-2mu NdWdis(tortal)=Wdis(ida)+Wdis(vuelta)=− − μ μ Nd− − μ μ Nd=− − 2μ μ Nd.0{displaystyle W_{dis}(total)=W_{dis}(ida)+W_{dis}(Vol)=-mu Nd-mu Nd=-2mu Nd<img alt="{displaystyle W_{dis}(total)=W_{dis}(ida)+W_{dis}(vuelta)=-mu Nd-mu Nd=-2mu Nd.

By contrast, if the force were conservative the total work done by force on the back and forth block (a cycle), it would be zero. It is the case of the work done to raise gradually (passing successive positions of balance) a mass body m{displaystyle m} a height h{displaystyle h} against gravity and then perform the work in the opposite direction, in favor of gravity, through the reverse path. Now, the total work, is void because they are equal and opposite jobs and there would be, loss of mechanical energy in the system.
Therefore, considering the work of the friction force on the block sliding down the rough surface, the mechanical energy Emec{displaystyle E_{mec}} of the body shall not be preserved:
<math alttext="{displaystyle Delta E_{mec}=W_{dis}=W_{no-conserv}Δ Δ Emec=Wdis=Wnor− − cornserv.0{displaystyle Delta E_{mec}=W_{dis}=W_{no-conserving}}0}<img alt="{displaystyle Delta E_{mec}=W_{dis}=W_{no-conserv} which corresponds to a decrease in the mechanical energy of the block.
Then the variation of the mechanical energy of a moving system is analyzed in a more general example, considering that the block is moved by an inclined plane of unpolished surface having, in an initial position, some kinetic energies Ec1{displaystyle E_{c1}} and potential due to weight Ep1{displaystyle E_{p1}} after having traveled a distance over the rough surface to a final position of energies Ec2{displaystyle E_{c2}} and Ep2{displaystyle E_{p2}} respectively. If mechanical energy is written as a sum of kinetic energies and potential due to the weight of the block, Emec=Ec+Ep{displaystyle E_{mec}=E_{c}+E_{p}}}the principle of energy conservation can be expressed as:
Ec2− − Ec1=Wcornserv+Wdis=Ep1− − Ep2+Wdis{displaystyle E_{c_{2}}-E_{c_{1}}}=W_{conserv}+W_{dis}=E_{p_{1}}}-E_{p_{2}}}or also, Emec2=Emec1+Wdis{displaystyle E_{mec_{2}}=E_{mec_{1}}.
Like <math alttext="{displaystyle W_{dis}Wdis.0{displaystyle W_{dis} implied}<img alt="{displaystyle W_{dis}, Emec1=Emec2+日本語Wdis日本語{displaystyle E_{mec_{1}}}=E_{mec_{2}}}}Or, Δ Δ Emec+日本語Wdis日本語=0{displaystyle Delta E_{mec}+ATAW_{display}
Thus, if the energy dissipated outside the system is also taken into account, the principle of conservation of energy leads to an energy balance in which the mechanical energy of a system subject to non-conservative forces, before suffering The interaction with the dissipative force is equal to the mechanical energy of the system after undergoing said interaction plus the energy dissipated abroad in the form of work of the dissipative force.
Other considerations of the principle of conservation of energy
The importance of the law of conservation of energy lies in the ability to analyze processes without directly considering the forces that act on the system or its movement as a consequence of them. There are other conservation laws analogous to the conservation of energy for the conservation of other physical magnitudes, one of them is the conservation of linear momentum and another is the conservation of angular momentum.
In general, these conservation principles have a different reading in classical mechanics and in quantum mechanics due to the continuous nature of matter at the macroscopic level and discrete at the microscopic level. Thus, in quantum mechanics, the energy of a photon is an integer multiple of Planck's constant, and electromagnetic energy is absorbed and emitted by bodies, in a similar way, in the form of quanta.
Three other conservation laws should be highlighted: the conservation of electric charge, that of baryons, and that of leptons. The first refers to the fact that the balance of positively charged and negatively charged particles in a physical system is always the same, even though these charged particles interact with each other. The second refers to the fact that, when two atomic nuclei interact with each other, the number of baryons after the interaction will always be equal to the number of baryons before the reaction. The conservation of leptons affirms that the same thing that happens with baryons, also happens with leptons, as experience confirms. In quantum mechanics, when the interactions between the different fundamental particles are analyzed, certain types of interaction are observed that are allowed and common, while others are prohibited. Those allowed are related to the laws of conservation, invariances or symmetries of the particles and that are associated with specific quantum numbers, in addition to the baryonic or lepton quantum number mentioned and collected by the standard model.
And finally, the concept of energy conservation is considered taking into account the notion of usable energy. The laws that govern useful energy are given by thermodynamics and incorporate the concept of entropy. Energy can be produced from a wide variety of sources: sun, rain, coal, etc. All of them are dependent on the energy received from the Sun. This energy production is governed by the First Law of thermodynamics (see below) which is the conservation of energy applied to systems of many particles, the molecules that make up matter. However, some of these transformations to produce useful energy present certain limitations, regulated by the Second Law of thermodynamics.
Energy in the movement of fluids
In physics, the principle of conservation of energy is very present to explain the phenomena that occur in nature and in particular when dealing with the movement of fluids (liquids and gases). When dealing with fluids in motion by conduction on the Earth's surface and to explain and calculate how their velocity changes when their height or pressure varies, Bernoulli's principle (1738) must be applied. It is a principle of conservation of energy applied to the fluid considered as a continuum, incompressible (with constant density) that ignores losses due to friction. Even considering ideal conditions, Bernoulli's equation is capable of explaining phenomena as important as the Venturi effect, the Magnus effect or aerodynamic lift.
Bernoulli's Equation
If an ideal fluid is considered that circulates through a conduction in a non-uniform way and the variation of kinetic energy and the variation of potential energy of a slice of it are analyzed in the time it takes to move from a position that will be called 1, to another position of the conduction that will be called 2, the equation of conservation of energy will be expressed:
this sum of variations of the kinetic energy and the potential energy of the system, is due to the work done on the two ends of the tube by the external fluid.
In order to obtain the Bernouilli equation, each term of the equation of the conservation of energy per unit of volume is developed, in the two positions 1 and 2 depending on its pressure, speed and height. The physical conditions for the: first slice are pressure p1{displaystyle p_{1}},speed v1{displaystyle v_{1}} and measured height regarding a given reference h1{displaystyle h_{1}}. For second pressure p2{displaystyle p_{2}},speed v2{displaystyle v_{2}} and height h2{displaystyle h_{2}}. If fluid density is ρ ρ {displaystyle rho }the conservation equation is then expressed as:
12ρ ρ Δ Δ V(v22− − v12)+ρ ρ Δ Δ Vg(h2− − h1)=A1p1Δ Δ s1− − A2p2Δ Δ s2{displaystyle {frac {1}{2}}{2}rho Delta V (v_{2}{2}{2}{1⁄2})+rho Delta V g (h_{2}-h_{1})=A_{1}{1} p_{1}Delta s_{1}{1}{2}{2}{2}{2}{2}{2}{1}{1}{1}{2}{2}{1}{1}{2}{2}{1⁄2}{2}{2}{1}{2}{1}{1}{1}{1}{1}{1}{1}{1⁄2}{1}{1}{1}{1⁄2}{2}{1}{1}{1}{1}{1}{1}{1}{1}{1⁄2}{1⁄2}{1⁄2}{1⁄2}{1⁄2}{1} Delta s_{2}}
This is because the variation of kinetic energy Δ Δ Ec{displaystyle Delta E_{c}} it is written as Δ Δ Ec=12Δ Δ mv22− − 12Δ Δ mv12{displaystyle Delta E_{c}={frac {1}{2}}}Delta m v_{2}^{2}-{frac {1}{2}}}}{1}}{2}}}{1}{2}}}{2}}}, the potential energy variation Δ Δ Ep{displaystyle Delta E_{p}} Like Δ Δ Ep=Δ Δ mgh2− − Δ Δ mgh1{displaystyle Delta E_{p}=Delta m gh_{2}-Delta m gh_{1}}}, due to the weight of the fluid slice (which has the same mass as passing from position 1 to position 2), to the difference of heights between the two slices and expressing the slice mass as Δ Δ m=ρ ρ Δ Δ V{displaystyle Delta m=rho Delta V}.
In addition, the total net work done on the fluid in the driving is Δ Δ W=F1Δ Δ s1− − F2Δ Δ s2{displaystyle Delta W=F_{1} Delta s_{1}-F_{2}Delta s_{2}}} due to the work performed by the external fluid at both ends of the driving and that the fluid located on the right side of point 2 exerts a force F2{displaystyle F_{2}} against displacement Δ Δ s2{displaystyle Delta s_{2}} being, therefore, his negative work. Finally, expressing strength as the product of pressure p{displaystyle p} by the cross section area A{displaystyle A}taking into account that the volume of the slice is Δ Δ V=AΔ Δ s{displaystyle Delta V=A Delta s and divide by Δ Δ V{displaystyle Delta V} In the three terms of the energy conservation equation, the Bernouilli equation is obtained:
p1− − p2=12ρ ρ (v22− − v12)+ρ ρ g(and2− − and1){displaystyle p_{1}-p_{2}={frac {1}{2}{2}rho (v_{2}{2}-v_{1}{2}})+rho g (y_{2}-y_{1}}}}}}}}}
Bernoulli's equation states that the work done on a unit volume of fluid by the surrounding fluid is equal to the sum of the changes in kinetic and potential energy per unit volume that occur during the process.
A more practical way of expressing the equation is as follows:
p1+ρ ρ gh1+12ρ ρ v12=p2+ρ ρ gh2+12ρ ρ v22=L=cte{displaystyle p_{1}+rho g h_{1}+{frac {1}{2}}}}rho v_{1}^{2}=p_{2}+rho g h_{2}+{frac}{1}{1}{2}{2}{2}{2}{2}{2} +rhocte}
It can be seen that all the terms in the above equation represent energy per unit volume. It can also be interpreted as an application of the principle of conservation of energy per unit volume to a fluid in motion.
First law of thermodynamics
The first principle of thermodynamics is a way of expressing the principle of conservation of energy when on a physical, solid, liquid or gas system, heat and work transfers are made from the outside of it. More specifically, it is usually applied to the operation of thermal machines, than when fed with a certain amount of heat. Q{displaystyle Q}, they are able to perform mechanical work W{displaystyle W}.
The use of the energy generated by a thermal machine both to produce a mechanical job, to generate electrical energy and to function as a cold machine, must, first of all, comply with the above-mentioned principle of energy conservation. Both the work done and the heat taken from the outside are manifested as variations of the internal energy of the system U{displaystyle U} (energy of the molecules that make up the system).
The first principle is expressed saying that heat Q{displaystyle Q} supplied to a thermal machine is used to perform a work W{displaystyle W} and to modify its internal energy U{displaystyle U},
First Principle of Thermodynamics: Q=W+Δ Δ U{displaystyle Q=W+Delta U}Where Δ Δ U{displaystyle Delta U} is the variation of the internal energy suffered by the system by exchanging heat and working with the outside.
The application of the First Law of Thermodynamics presents some restrictions expressed in the second law of thermodynamics that establish an added limit to the maximum production of work. The limit imposed by the Second Law gives rise to the reversible heat engine, distinguishing it, in turn, from the non-reversible one, with lower performance.
For a possible practical application of these two principles, one could turn to power generating equipment. In thermal power plants, heat is produced by the combustion of a fuel (coal, oil, gas, etc.). In nuclear power plants, heat is produced from nuclear energy. In both cases there is a fluid (water) that is heated until it is transformed into very hot steam. The steam drives a turbine producing work. The residual steam has cooled and leaves the turbine, but it still has an increase in internal energy relative to the water that was heated. This increase in internal energy does not generate work and is eliminated abroad, cooling the steam until the water is recovered, which is ready for further heating.
The reasoning of the previous paragraph has consisted of an application of the First Law of Thermodynamics. The reasoning can be continued by applying the principle of conservation of energy, noting that the work developed by the turbine is transmitted in the plant itself to an alternator. The alternator generates electrical energy that is distributed to users through an electrical network. Users will transform electrical energy into work, heat or other types of energy.
Energy in vibratory movements
Energy in simple harmonic motion
To analyze the simplest oscillatory movement, the M.A.S., is considered the most basic system: a small mass body m{displaystyle m} oscillating at the end of a resort, despicable mass and constantly recovering k{displaystyle k}placed horizontally. Assuming that the air does not offer appreciable resistance to the movement of the mass subject to the spring, the recovery force of the spring is the only horizontal force (according to the direction of the axis x{displaystyle x}) that acts on the body and in first approximation obeys the Hooke law Fx=− − kx{displaystyle F_{x}=-kx}with its balance position in x=0{displaystyle x=0}. Being the elastic force F{displaystyle F} a conservative force, the dock mass system has an elastic potential energy [section 5.3.3], so that the mechanical energy of the system Em=Ec+Ep{displaystyle E_{m}=E_{c}+E_{p}}} It's constant. The kinetic energy of the body is Ec=12mv2{displaystyle E_{c}={1over 2}mv^{2}}} and the potential energy of the spring, when you are stretched or compressed a distance x{displaystyle x}is as seen in the section of potential elastic energy (5.3.3): Ep=12kx2{displaystyle E_{p}={1over 2}kx^{2}}}. Because there are no friction forces that do a job, the mechanical energy is preserved and is a constant:
Em=12mv2+12kx2=cornstante{displaystyle E_{m}={1 over 2}mv^{2}+{1 over 2}kx^{2}=constant}The energy is related to the breadth, A{displaystyle A}of the generated movement. When the movement of the mass over the balance position is maximum, x=A{displaystyle x=A} being A{displaystyle A} the amplitude of the movement, the potential energy is maximum Ep=12kA2{displaystyle E_{p}={1over 2}kA^{2}}} and proportional to the width to the square, and the kinetic energy is zero, since its speed is v=vx=0{displaystyle v=v_{x}=0}. Therefore, in that position, mechanical energy is only of potential origin, Em=12kA2{displaystyle E_{m}={1over 2}kA^{2}}}. Therefore:
Em=12mv2+12kx2=12kA2=cornstante{displaystyle E_{m}={1 over 2}mv^{2}+{1 over 2}kx^{2}={1 over 2}kA^{2}=constant}From this equation you can deduce the expression of the speed v=vx{displaystyle v=v_{x}} for any displacement of x:
vx=± ± km(A2− − x2){displaystyle v_{x}=pm {sqrt {{k over m}(A^{2}-x^{2}}}}}}}}}}}On the other hand, you can see that the maximum speed is obtained for x=0{displaystyle x=0}. Calling ω ω =km{displaystyle {omega }={sqrt {k over m}}}}It follows: vmax=ω ω A{displaystyle v_{max}=omega A}. According to the new notation, the mass oscillates with a speed between − − ω ω A{displaystyle} and +ω ω A{displaystyle +omega A}. The physical magnitude described by ω ω {displaystyle omega }, which is measured in cycles/s, receives the natural pulsation name of the M.A.S.
Energy in damped oscillations. Loss of energy due to friction
In oscillatory movements the friction forces inevitably appear, so that the oscillation is damped with time and ends up extinct, giving rise to the damped oscillations. In addition to the conservative recovery force proper to the harmonic movements Fx=− − kx{displaystyle F_{x}=-kx}, appears a buffering force that is not conservative. It is not difficult to understand the existence of this force, since in practice it is observed its appearance, for example in a pendulum clock or in a bell. They are mechanical systems where their respective movements of oscillation do not last forever: in them there appears a force that acts against the movement and that slows it gradually. This leads to the conclusion that the mechanical energy of this type of system is not constant, but decreases over time, due precisely to the work of that non-conservative force that cushions the oscillation. The work of the friction forces of the oscillating system, either due to the friction with the air, either due to the friction between its own operating mechanisms (friction between the gears of a watch), to its axis of sustainability (iscillation of a bell) or to a combination of all of them, in short, consumes an energy. This energy ends, in most cases, dissipating outside the system in the form of heat. The buffering or friction force F→ → dis{displaystyle {vec {F}}_{displaystyle}} which appears between a solid body and a fluid within which it moves can be expressed as: F→ → dis=Fdxi→ → =− − bvxi→ → {displaystyle {vec {F}}_{dis}=F_{d_{x}}{vec {i}}}}{=-bv_{x}{vec {i}}}}}}}in which b{displaystyle b} is the constant proportionality that reflects the intensity of the buffering force and vx{displaystyle v_{x}} the speed of the body in the direction of the movement. Note that the friction force carries the same direction as the speed, is proportional to it and, in addition, it is of opposite sense to it. Incorporating the friction force, applying Newton's second law is obtained:
␡ ␡ Fx=− − kx− − bvx=max[chuckles]1]{displaystyle sum F_{x}=-kx-bv_{x}=ma_{x}qquad} [1]Other expressions can be deduced from this expression, including the law of damped harmonic motion. In particular, the deduction of the loss of mechanical energy is of interest. It is known that, at any instant, the mechanical energy is equal to:
Em=12mvx2+12kx2[chuckles]2]{displaystyle E_{m}={{1over 2}mv_{x}^{2} +{{{1over 2}kx^{2}}qquad [2]}where the first addend is the kinetic energy and the second addend is the potential energy. If the expression is derived with respect to time:
dEmdt=mvxdvxdt+kxdxdt[chuckles]3]{displaystyle {{dE_{m} over dt}=mv_{x}{dv_{x} over dt}+kx{dx over dt}}qquad [3]}Since the derivative of velocity with respect to time is acceleration, and the derivative of position with respect to time is velocity, it follows:
dEmdt=vx(max+kx)[chuckles]4]{displaystyle {{dE_{m} over dt}=v_{x};(ma_{x}+kx}}qquad [4]}}From [1] it is obtained:− − bvx=max+kx{displaystyle -b;v_{x}=ma_{x}+kx}. And finally:
dEmdt=vx(− − bvx)=− − bvx2[chuckles]5]{displaystyle {{dE_{m} over dt}=v_{x};(-b;v_{x})=-bv_{x}^{2}qquad [5]}It follows that, whatever the sense of speed, the energy of the oscillatory system decreases. The oscillations are decreasing from breadth, losing their energy until, in the end, it stops. Also, knowing that mechanical power Pm{displaystyle P_{m}} is: <math alttext="{displaystyle P_{m}={dE_{m} over dt}=-b;v_{x}^{2}Pm=dEmdt=− − bvx2.0{displaystyle P_{m}={dE_{m} over dt}=-b;v_{x}^{2}{2}{2}{cH00}<img alt="{displaystyle P_{m}={dE_{m} over dt}=-b;v_{x}^{2}and can also be expressed as:<math alttext="{displaystyle P_{m}={dE_{m} over dt}={vec {F_{d}}};.{vec {v}}=F_{d_{x}};v_{x}=-b;v_{x}^{2}Pm=dEmdt=Fd→ → .v→ → =Fdxvx=− − bvx2.0{displaystyle P_{m}={dE_{m} over dt}={vec {F_{d}}}}{;.{vec {v}}=F_{d_{x}}}}{;v_{x}=-b;v_{x}{x}{2}{2}{}{x}}}}}}{x<img alt="{displaystyle P_{m}={dE_{m} over dt}={vec {F_{d}}};.{vec {v}}=F_{d_{x}};v_{x}=-b;v_{x}^{2}. This expression is the dampening power of the movement or dissipative power due to the friction force, which represents the speed with which the damping force acts and, therefore, the speed with which the mechanical energy of the system is reduced due to friction.
Technologies associated with mechanical energy
Some types of mechanical energy are:
- Hydraulic energy: water drops and takes advantage of the potential energy obtained. It is used to generate electric energy and to move flour mills.
- Wind energy: produced by winds generated in the Earth's atmosphere. It is used to generate electric energy, such as groundwater extraction mechanism or certain types of mills for agriculture. It's a kind of kinetic energy.
- Energy dizziness: product of the movement of the tides and waves of the sea, is a type of kinetic energy.
Contenido relacionado
Edme Mariotte
Magnetic susceptibility
Diode



















































































































































































































![{displaystyle sum F_{x}=-kx-bv_{x}=ma_{x}qquad [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb31c666565ad487e2262406b853a0411c9bc06b)
![{displaystyle E_{m}={{1 over 2}mv_{x}^{2}}+{{1 over 2}kx^{2}}qquad [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/111dce8484d1e4b0751a83ec6935afb060d9a94f)
![{displaystyle {{dE_{m} over dt}=mv_{x}{dv_{x} over dt}+kx{dx over dt}}qquad [3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e3821d8b6514e4287f221470e89b0820f3c49be)
![{displaystyle {{dE_{m} over dt}=v_{x};(ma_{x}+kx)}qquad [4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e743ca4c856b4884081fadb58b876af1d90e3e43)

![{displaystyle {{dE_{m} over dt}=v_{x};(-b;v_{x})=-bv_{x}^{2}}qquad [5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54e2b320d32756157011f48b54c527a920f81bf6)
