Maxwell's equations
The Maxwell equations are a set of four equations (originally 20 equations) that fully describe electromagnetic phenomena. The great contribution of James Clerk Maxwell was to bring together in these equations long years of experimental results, due to Coulomb, Gauss, Ampere, Faraday and others, introducing the concepts of field and displacement current, unifying electric and magnetic fields in a single concept.: the electromagnetic field.
Historical development of Maxwell's equations
Since the late 18th century, various scientists formulated quantitative laws that related the interactions between electric fields, magnetic fields, and currents on conductors. Among these laws are Ampère's law, Faraday's law or Lenz's law. Maxwell would manage to unify all these laws in a coherent description of the electromagnetic field.
Maxwell realized that conservation of electric charge seemed to require introducing an additional term into Ampère's law. In fact, one of the most important aspects of Maxwell's work on electromagnetism is now considered to be the term he introduced into that law: the time derivative of an electric field, known as displacement current. The work that Maxwell published in 1865, A Dynamical Theory of the Electromagnetic Field, modified the version of Ampère's law with which the existence of electromagnetic waves propagating, depending on the material medium, was predicted. speed of light in said medium. In this way Maxwell identified light as an electromagnetic wave, thus unifying optics with electromagnetism.
Except for the modification to Ampère's law, none of the other equations were original. What Maxwell did was to re-obtain these equations from mechanical and hydrodynamic models using his Faraday line-of-force vortex model.
In 1884, Oliver Heaviside along with Willard Gibbs grouped these equations and reformulated them in the current vector notation. However, it is important to know that in doing so, Heaviside used temporary partial derivatives, different from the total derivatives used by Maxwell, in the equation (54). This led to the loss of the term v× × B{displaystyle vtimes B} which appeared in the subsequent equation of Maxwell's work (number 77). Today, this term is used as a complement to these equations and is known as Lorentz's force.
The story is still unclear, because the term Maxwell's equations is also used for a set of eight equations in Maxwell's 1865 publication, A Dynamical Theory of the Electromagnetic Field, and this confusion is due to the fact that six of the eight equations are written as three equations for each coordinate axis, so one can get confused by finding twenty equations with twenty unknowns. The two types of equations are nearly equivalent, despite Heaviside's removal of the term from the current four equations.
Detail of the equations
Gauss's law for the electric field
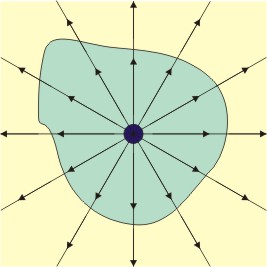
The law of Gauss explains the relationship between the flow of the electric field through a closed surface with the net load enclosed by that surface. It is defined as electric flow (≈ ≈ E{displaystyle Phi _{E},}) to the amount of electrical fluid that crosses a given surface. Analogous to the flow of fluid mechanics, this electrical fluid does not transport matter, but helps to analyze the amount of electric field (E→ → {displaystyle {vec {E}}) that passes through an S surface. Mathematically expressed as:
- ≈ ≈ E=♫ ♫ SE→ → ⋅ ⋅ dS→ → {displaystyle Phi _{E}=oint _{S}{vec {E}{cdot d{vec {S}}}}}}
The law says that the flow of the electric field through a closed surface is equal to the quotient between the load (q) or the sum of the loads inside the surface and the electric permitivity in the vacuum (ε ε 0{displaystyle varepsilon}), like:
- ♫ ♫ SE→ → ⋅ ⋅ dS→ → =qε ε 0{displaystyle oint _{S}{vec {E}}}{cdot d{vec {S}}}{frac {q}{varepsilon _{0}}}}}}}}}
The differential form of Gauss's law, locally, states that by the Gauss-Ostrogradsky theorem, the divergence of the electric field is proportional to the electric charge density, that is,
- ► ► → → ⋅ ⋅ E→ → =ρ ρ ε ε 0{displaystyle {vec {nabla}}cdot {vec {E}}={frac {rho }{varepsilon _{0}}}}}}}}}}
where ρ ρ {displaystyle rho } is the load density in the inner medium to the closed surface. Intuitively means that the E field diverges or departs from a load ρ ρ ε ε 0{displaystyle {frac {rho }{varepsilon _{0}}}}, which is graphically portrayed as vectors that come from the source that generates them in all directions. By convention if the value of the expression is positive then the vectors come out, if it is negative these enter the load.
For general cases an amount called electricity flow density must be introduced (D→ → {displaystyle {vec {D}}}) and our expression gets the form:
- ► ► → → ⋅ ⋅ D→ → =ρ ρ {displaystyle {vec {nabla}}cdot {vec {D}}=rho }
Gauss's law for the magnetic field
Experimentally, the result was reached that magnetic fields, unlike electric ones, do not begin and end at different charges. This law primarily indicates that the magnetic field lines must be closed. In other words, it is said that on a closed surface, whatever it may be, we will not be able to enclose a source or sink of field, this expresses the non-existence of the magnetic monopole. By enclosing a dipole in a closed surface, no magnetic flux enters or leaves, therefore the magnetic field does not diverge, it does not leave the surface. So the divergence is zero. Mathematically this is expressed like this:
- ► ► → → ⋅ ⋅ B→ → =0{displaystyle {vec {nabla}}cdot {vec {B}=0}
where B→ → {displaystyle {vec {B}}} is magnetic flow density, also called magnetic induction. It is clear that divergence is zero because field vectors do not come out or enter, but it does closed paths. The field does not diverge, i.e. the divergence of B is null.
Its equivalent integral form:
- ♫ ♫ SB→ → ⋅ ⋅ dS→ → =0{displaystyle oint _{S}{vec {B}}}cdot d{vec {S}}=0}
As in the integral form of the electric field, this equation only works if the integral is defined on a closed surface.
Faraday-Lenz Law
Faraday's law tells us about electromagnetic induction, which causes an electromagnetic force in a magnetic field. It is usual to call Faraday-Lenz's law in honor of Heinrich Lenz as the least sign comes from the Law of Lenz. It is also called Faraday-Henry's law, because Joseph Henry discovered this induction separately to Faraday but almost simultaneously. The first thing to introduce is the electromotric force (E{displaystyle {mathcal {E}}}), if we have a variable magnetic field with time, an electromotric force is induced in any electrical circuit; and this force is equal to less the temporary derivative of magnetic flow, thus:
- E=− − dφ φ Bdt{displaystyle {mathcal {E}}=-{frac {dphi _{B}{dt}}}}}}},
since the magnetic field is dependent on the position we have that the magnetic flux is equal to:
- φ φ B=∫ ∫ SB→ → ⋅ ⋅ dS→ → {displaystyle phi _{B}=int _{S}{vec {B}}}{cdot d{vec {S}}}}}.
In addition, the fact that there is an electromotive force indicates that there is an electric field that is represented as:
- E=♫ ♫ CE→ → ⋅ ⋅ dl l → → {displaystyle {mathcal {E}}=oint _{C}{vec {E}}cdot d{vec {ell }}}}}}}
with which we finally obtain the expression of Faraday's law:
- ♫ ♫ CE→ → ⋅ ⋅ dl l → → =− − ∫ ∫ SdB→ → dt⋅ ⋅ dS→ → {displaystyle oint _{C}{vec {E}}}cdot d{vec {vec {vec}}}=-int _{S}{d{vec {B}}} over dt}{cdot d{vec {S}}}}}}{
This indicates that a magnetic field that depends on time implies the existence of an electric field, whose circulation through an arbitrary closed path is equal to minus the time derivative of the magnetic flux on any surface bounded by the closed path.
The negative sign explains that the direction of the induced current is such that its flow opposes the cause that produces it, thus compensating for the variation in magnetic flux (Lenz's Law).
The local differential form of this equation is:
- ► ► → → × × E→ → =− − ▪ ▪ B→ → ▪ ▪ t{displaystyle {vec {cHFFFF}}{vec {E}}}=-{frac {partial {B}}}{partial t}}}}}
That is, the curl of the electric field is the partial derivative of the magnetic induction with respect to time.
It is interpreted as follows: if there is a variation of the magnetic field B then this causes an electric field E or the existence of an unsteady magnetic field in free space causes circulations of the vector E along closed lines. In the presence of free charges, such as electrons, the E field can displace charges and produce an electric current. This equation relates the electric and magnetic fields, and has other practical applications such as electric motors and electric generators and explains their operation. More precisely, it shows that a voltage can be generated by varying the magnetic flux through a given surface.
Generalized Ampère's Law
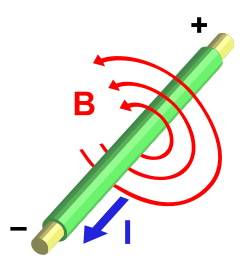
Ampère formulated a relationship for a still magnetic field and an electric current that does not vary in time. The law of Ampère says that the circulation in a magnetic field (B→ → {displaystyle {vec {B}}}) along a closed curve C is equal to current density (J→ → {displaystyle {vec {J}}}) on the surface enclosed in curve C, mathematically like this:
- ♫ ♫ CB→ → ⋅ ⋅ dl l → → =μ μ 0∫ ∫ SJ→ → ⋅ ⋅ dS→ → {displaystyle oint _{C}{vec {B}}}cdot d{vec {vec {vec}}}=mu _{0}int _{S}{vec {J}}}{cdot d{vec {S}}}}}}
where μ μ 0{displaystyle mu _{0}} is the magnetic permeability in the vacuum.
But when this relationship is considered with fields that do vary over time, it leads to erroneous calculations, such as violating charge conservation. Maxwell corrected this equation to adapt it to non-stationary fields and was later able to be verified experimentally by Heinrich Rudolf Hertz.
Maxwell rephrased this law as follows:
- ♫ ♫ CB→ → ⋅ ⋅ dl l → → =μ μ 0∫ ∫ SJ→ → ⋅ ⋅ dS→ → +μ μ 0ε ε 0ddt∫ ∫ SE→ → ⋅ ⋅ dS→ → {cdot mathrm {d} {vec}{cdot mathrm {d} {vec {ell }}=mu _{0}{s}{s}{vec}{cdot mathrm {d} {d} {s}{s}{0}{m}{s}{.
In the specific stationary case this relationship corresponds to Ampère's law, it also confirms that an electric field that varies with time produces a magnetic field and it is also consistent with the principle of conservation of charge.
In differential form, this equation takes the form:
- ► ► → → × × B→ → =μ μ 0J→ → +μ μ 0ε ε 0▪ ▪ E→ → ▪ ▪ t{displaystyle {vec {nabla}}times {vec {B}}=mu _{0}{vec {J}}+mu _{0},varepsilon _{0}{frac {partial {vec {E}}}}{partial t}}}}}{.
In a simple way, this equation explains that if there is a conductor, a straight wire through which a current density J circulates, this causes the appearance of a rotational magnetic field B around the wire and that the rotor of B points in the same sense as J.
In material means
In the case that the charges are in material media, and assuming that these are linear, homogeneous, isotropic and non-dispersive, a relationship can be found between the electric intensity and magnetic induction vectors by means of two parameters known as electric permittivity and magnetic permeability:
- D→ → =ε ε E→ → =ε ε 0ε ε rE→ → {displaystyle {vec {D}}=varepsilon {vec {E}}}=varepsilon _{0}varepsilon _{r}{vec {E}}}}}}}}
- B→ → =μ μ H→ → =μ μ 0μ μ rH→ → {displaystyle {vec {B}}{vec {vec {H}}}}=mu _{0}{r}{vec {H}}}}}}}}
But these values also depend on the material environment, so it is said that a medium is linear when the relationship between E/D and B/H is linear. If this relationship is linear, mathematically you can say that ε ε {displaystyle varepsilon } and μ μ {displaystyle mu } are represented by a 3x3 matrix. If a medium is isotrope is because this matrix has been diagonally and consequently is equivalent to a function ε ε (x,and,z){displaystyle varepsilon (x,y,z)}; if in this diagonal one of the elements is different from the other one is said to be an anisotropic medium. These elements are also called dielectric constants and, when these constants do not depend on their position, the medium is homogeneous.
Values ε ε {displaystyle varepsilon } and μ μ {displaystyle mu } in linear media do not depend on the intensity of the field. On the other hand, allowivity and permeability are scalars when the loads are in homogeneous and isotropic means. Heterogeneous and isotropical means depend on the coordinates of each point so the values, scales, will depend on the position. The anisotropic media are tensors. Finally, in the void so much ρ ρ {displaystyle rho } Like J→ → {displaystyle {vec {J}}} It's zero because we assume there's no sources.
In the following table we find the equations as they are formulated in a vacuum and in matter.
| In the void | In the field |
|---|---|
| ► ► → → ⋅ ⋅ E→ → =ρ ρ ε ε 0{displaystyle {vec {nabla}}cdot {vec {E}}={frac {rho }{varepsilon _{0}}}}}}}}}} | ► ► → → ⋅ ⋅ D→ → =ρ ρ {displaystyle {vec {nabla}}cdot {vec {D}}=rho } |
| ► ► → → ⋅ ⋅ B→ → =0{displaystyle {vec {nabla}}cdot {vec {B}=0} | ► ► → → ⋅ ⋅ B→ → =0{displaystyle {vec {nabla}}cdot {vec {B}=0} |
| ► ► → → × × E→ → =− − ▪ ▪ B→ → ▪ ▪ t{displaystyle {vec {cHFFFF}}{vec {E}}}=-{frac {partial {B}}}{partial {t}}}}}}}}} | ► ► → → × × E→ → =− − ▪ ▪ B→ → ▪ ▪ t{displaystyle {vec {cHFFFF}}{vec {E}}}=-{frac {partial {B}}}{partial {t}}}}}}}}} |
| ► ► → → × × B→ → =μ μ 0J→ → +μ μ 0ε ε 0▪ ▪ E→ → ▪ ▪ t{displaystyle {vec {nabla}}times {vec {B}}{mu _{0}{vec {J}}+mu _{0}varepsilon _{0}{frac {partial {vec {E}}}{partial t}}}}}{ | ► ► → → × × H→ → =J→ → +▪ ▪ D→ → ▪ ▪ t{displaystyle {vec {nabla}}times {vec {H}}}={vec {J}+{frac {partial {vec {D}}}}{partial {t}}}}}}}} |
Maxwell's Equations
Maxwell's equations as we now know them are the four mentioned above and as a summary they can be found in the following table:
| Name | Differential form | Integral form |
|---|---|---|
| Law of Gauss: | ► ► → → ⋅ ⋅ E→ → =ρ ρ ε ε 0{displaystyle {vec {nabla}}cdot {vec {E}}={frac {rho }{varepsilon _{0}}}}}}}}}} | ♫ ♫ SE→ → ⋅ ⋅ dS→ → =qε ε 0{displaystyle {underset {S}{oint }}{vec {E}}{cdot mathrm {d} {vec {S}}}{frac {q}{varepsilon _{0}}}}}} |
| Law of Gauss for the magnetic field: | ► ► → → ⋅ ⋅ B→ → =0{displaystyle {vec {nabla}}cdot {vec {B}=0} | ♫ ♫ SB→ → ⋅ ⋅ dS→ → =0{displaystyle oint _{S}{vec {B}}}cdot mathrm {d} {vec {s}}=0} |
| Faraday Law: | ► ► → → × × E→ → =− − ▪ ▪ B→ → ▪ ▪ t{displaystyle {vec {cHFFFF}}{vec {E}}}=-{frac {partial {B}}}{partial t}}}}} | ♫ ♫ CE→ → ⋅ ⋅ dl l → → =− − ddt∫ ∫ SB→ → ⋅ ⋅ dS→ → {displaystyle oint _{C}{vec {E}}}{cdot d{vec {vec {vec}}}=- {d over dt}int _{s}{vec {B}}}{cdot d{vec {S}}}}}}}{ |
| Generalized Law of Ampère: | ► ► → → × × B→ → =μ μ 0J→ → +μ μ 0ε ε 0▪ ▪ E→ → ▪ ▪ t{displaystyle {vec {nabla}}times {vec {B}}=mu _{0}{vec {J}}+mu _{0},varepsilon _{0}{frac {partial {vec {E}}}}{partial t}}}}}{ | ♫ ♫ CB→ → ⋅ ⋅ dl l → → =μ μ 0∫ ∫ SJ→ → ⋅ ⋅ dS→ → +μ μ 0ε ε 0ddt∫ ∫ SE→ → ⋅ ⋅ dS→ → {displaystyle oint _{C}{vec {B}}{cdot d{vec {vec}{vec}{vec}{cdot d{vec}{s}}{s}{s}{s}{s}}{s}{s}{s}{s}{s}}{s}} |
These four equations along with Lorentz's force are those that explain any type of electromagnetic phenomenon. The importance of Maxwell's equations is that they remain invariant with any unit system, except with small exceptions, and are compatible with special and general relativity. Plus Maxwell discovered that the amount c=1ε ε 0μ μ 0{displaystyle c={frac {1}{sqrt {varepsilon _{0},mu _{0}}}}}}} was simply the speed of light in the vacuum, so light is a form of electromagnetic radiation. The values currently accepted for the speed of light, permitivity and magnetic permeability are summarized in the following table:
| Symbol | Name | Numerical value | Measurement unit SI | Type |
|---|---|---|---|---|
| c{displaystyle c } | Speed of light in the vacuum | 2.99792458× × 108{displaystyle 2.99792458times 10^{8}} | meters per second | defined |
| ε ε 0{displaystyle varepsilon} | Vacuum permitivity | 8.854× × 10− − 12{displaystyle 8.854times 10^{-12} | by subway | derivative |
| μ μ 0{displaystyle mu _{0} } | MRI | 4π π × × 10− − 7{displaystyle 4pi times 10^{-7}} | per metre | defined |
Scalar potential and vector potential
As a mathematical consequence of Maxwell's equations and also with the aim of simplifying their calculations the concepts of vector potential have been introduced (A→ → {displaystyle {vec {A}}}) and potential scale (≈ ≈ {displaystyle Phi }). This vector potential is not unique and has no clear physical meaning but it is known that an infinitesimal element of current gives rise to a contribution dA→ → {displaystyle mathrm {d} {vec {A}}} parallel to the current. This potential is obtained as a result of the law of Gauss for magnetic flow, since it is known that if the divergence of a vector is zero, that vector as a consequence defines a rotational, as well:
- ► ► ⋅ ⋅ B→ → =► ► ⋅ ⋅ (► ► × × A→ → )=0{displaystyle nabla cdot {vec {B}}=nabla cdot (nabla times {vec {A}})=0}
- B→ → =► ► × × A→ → {displaystyle Longleftrightarrow quad {vec {B}}}=nabla times {vec {A}}}}
From this vector potential and Faraday's law, a scalar potential can be defined as follows:
► ► × × E→ → =− − ▪ ▪ B→ → ▪ ▪ t► ► × × E→ → +▪ ▪ ▪ ▪ t(► ► × × A→ → )=0► ► × × (E→ → +▪ ▪ A→ → ▪ ▪ t)=0 − − ► ► ≈ ≈ =E→ → +▪ ▪ A→ → ▪ ▪ t{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFF00} {cHFFFFFFFF00} {cHFFFFFFFF}{cHFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFFFFFF}{cHFFFFFFFFFFFFFF}{cHFFFFFFFFFF}{cHFF}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF} {cHFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00} {cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF} {cHFFFFFFFFFFFFFFFFFFFF
where the sign less (− − {displaystyle}It's a convention. These potentials are important because they have a gauge symmetry that gives us some freedom when choosing them. The electric field depending on the potentials:
- E→ → =− − ► ► ≈ ≈ − − ▪ ▪ A→ → ▪ ▪ t{displaystyle {vec {E}}=-nabla Phi -{frac {partial {vec {A}}}{partial {t}}}}}}
We find that with the introduction of these quantities Maxwell's equations are reduced to only two, since Gauss's law for the magnetic field and Faraday's law are satisfied by definition. Thus Gauss's law for the electric field written in terms of potentials:
− − ► ► 2≈ ≈ − − ▪ ▪ ▪ ▪ t(► ► ⋅ ⋅ A→ → )=ρ ρ ε ε 0{displaystyle}{nabla ^{2}Phi -{cfrac {partial}{partial t}}(nabla cdot {vec {A}}})={cfrac {rho }{varepsilon _{0}}}}}}{
and generalized ampere's law
► ► (► ► ⋅ ⋅ A→ → )− − ► ► 2A→ → =μ μ 0J→ → − − μ μ 0ε ε 0▪ ▪ ▪ ▪ t(► ► ≈ ≈ +▪ ▪ A→ → ▪ ▪ t){displaystyle nabla (nabla cdot {vec {A}}})-nabla ^{2}{vec {A}}{mu _{0}{vec {J}{abi}{are}{0}{varepsilon _{0}{frac {partial}{bigg}{ !.
Notice that we have gone from a set of four first-order partial differential equations to only two second-order partial differential equations. However, these equations can be simplified with the help of a proper choice of gauge.
Physical consequences of the equations
Principle of conservation of charge
Maxwell's equations have implied the principle of load conservation. The principle states that the electrical load is neither created nor destroyed, globally or locally, but is transferred only; and that if on a closed surface the load contained within it is diminishing, there must be a net current flow to the outside of the system. That is to say load density ρ ρ {displaystyle mathbf {rho } } and current density → → {displaystyle {vec {jmath}}} satisfy an equation of continuity.
From the differential form of Ampère's law we have:
► ► → → ⋅ ⋅ (► ► → → × × B→ → )=μ μ 0► ► → → ⋅ ⋅ J→ → +μ μ 0ε ε 0▪ ▪ ▪ ▪ t(► ► → → ⋅ ⋅ E→ → ){cHFFFFFF} {cHFFFF}{cHFFFFFF} {cHFFFFFF}{cH00FF} {cHFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFF}{cHFF}{cH00}{cH00}{cH00}{cH00} {cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF} {cHFFFFFFFFFFFFFFFFFF} {cHFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00} {cH00} {cHFFFFFFFFFFFFFFFFFFFF} {cH00} {cH00} {cH} {cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
that by replacing the law of Gauss and taking into account that ► ► → → ⋅ ⋅ (► ► → → × × A→ → )=0{displaystyle {vec {nabla}}cdot left({vec {nabla}}}}times {vec {A}}right)=0} (for any vector) A→ → {displaystyle {vec {A}}}), you get:
0=► ► → → ⋅ ⋅ J→ → +▪ ▪ ρ ρ ▪ ▪ t{displaystyle 0={vec {nabla }}{cdot {vec {J}+}{frac {partial rho }{partial t}}}}}}}}
or in an integral way: 0=♫ ♫ SJ→ → ⋅ ⋅ dS→ → +dqdt{displaystyle 0=oint _{S}{vec {J}}{cdot mathrm {d} {vec {s}}}{mathrm {d}}{mathrm {d}}}}}}{mathrm {d}}}}}}}}}.
Maxwell's original equations
In chapter III of A Dynamical Theory of the Electromagnetic Field, titled "General Equations of the Electromagnetic Field", Maxwell formulated eight equations that he named A through H. These equations came to may be known as "Maxwell's equations," but now this epithet goes to the equations that Heaviside put together. Heaviside's version of Maxwell's equations actually contains only one equation of the original eight, Gauss's law, which in the set of eight would be equation G. Furthermore, Heaviside merged Maxwell's A equation of total current with the circuital law of Ampère which in Maxwell's work was equation C. This fusion, which Maxwell himself published in his 1861 work On Physical Lines of Force modifies Ampère's circuital law to include the current of Maxwell's displacement.
The eight original Maxwell equations can be written in vector form as follows:
| Denomination | Name | Equation |
|---|---|---|
| A | Current displacement | J→ → tort=J→ → +▪ ▪ D→ → ▪ ▪ t{displaystyle {vec {J}}_{rm {tot}}}={vec {J}}}+{frac {partial {vec {D}}}{partial t}}}}}} |
| B | Magnetic force equation | μ μ H→ → =► ► → → × × A→ → {displaystyle mu {vec {H}}={vec {nabla}}{times {vec {A}}}}} |
| C | Circuital Law of Ampère | ► ► → → × × H→ → =J→ → tort{displaystyle {vec {nabla}}times {vec {H}}={vec {J}_{rm {tot}}}}} |
| D | Lorentz Force | E→ → =μ μ v→ → × × H→ → − − ▪ ▪ A→ → ▪ ▪ t− − ► ► φ φ {displaystyle {vec {E}}=vec {v}}times {vec {H}}}-{frac {partial {vec {A}}}}{partial t}}-nabla phi } |
| E | Elastic electricity equation | E→ → =1ε ε D→ → {displaystyle {vec {E}}={frac {1}{varepsilon }{vec {D}}}}}{ |
| F | Ohm Law | E→ → =1σ σ J→ → {displaystyle {vec {E}}={frac {1}{sigma }{vec {J}}}}} |
| G | Law of Gauss | ► ► → → ⋅ ⋅ D→ → =ρ ρ {displaystyle {vec {nabla}}cdot {vec {D}}=rho } |
| H | Continuity of cargo equation | ► ► → → ⋅ ⋅ J→ → =− − ▪ ▪ ρ ρ ▪ ▪ t{displaystyle {vec {nabla}}cdot {vec {J}}=-{frac {partial rho }{partial t}}}}}}} |
where: H→ → {displaystyle {vec {H}}} is the magnetic field intensity vector (called by Maxwell as Magnetic intensity); J→ → {displaystyle {vec {J}}} is electrical current density and J→ → tort{displaystyle {vec {J}_{rm {tot}}}} is the total current including the flow of displacement; D→ → {displaystyle {vec {D}}} is the field displacement (electric displacement); ρ ρ {displaystyle rho } is free load density (free electricity quantity); A→ → {displaystyle {vec {A}}} is the magnetic potential vector (magnetic impulse); E→ → {displaystyle {vec {E}} is the electric field (electric force [not to confuse with the current definition of electromotric force]); φ φ {displaystyle phi } is the electric potential σ σ {displaystyle sigma } is electrical conductivity (specific resistance, now only resistance).
Maxwell did not consider material media in general, this initial formulation uses permittivity and permeability in linear, isotropic, and nondisperse media, although they can also be used in anisotropic media.
Maxwell included the term μ μ v→ → × × H→ → {displaystyle mu {vec {v}}times {vec {H}}}} in the expression of the electromotric force of the D equation, which corresponds to the magnetic force per unit of load in a conductor that moves at a speed v→ → {displaystyle {vec {v}}}. This means that equation D is another formulation of Lorentz's force. This equation first appeared as the 77th equation of the publication On Physical Lines of Force Maxwell, prior to the publication of Lorentz. At present this Lorentz force is not part of Maxwell's equations but it is considered a fundamental additional equation in electromagnetism.
Expression of the equations in relativity
In special relativity, Maxwell's equations in a vacuum are written using geometric relations, which take the same form in any inertial reference frame. These equations are written in terms of quadrivectors and contravariant tensors, which are geometric objects defined in M4. These objects are related by means of differential forms in geometric relations that, when expressed in components of the Lorentz coordinate systems, provide the equations for the electromagnetic field.
The quadrilateral Jα α {displaystyle ,J^{alpha}} is described by a 1-form and carries information on the distribution of loads and currents. Its components are:
- Jα α =(cρ ρ (r,t),J(r,t)){displaystyle ,J^{alpha }=(crho (mathbf {rt}),mathbf {J} (mathbf {r})}}
That the following geometric relation must satisfy so that the continuity equation is fulfilled.
- δ δ J=0{displaystyle ,delta J=0}
Written in components of the Lorentz coordinate systems is:
- ▪ ▪ α α Jα α =0{displaystyle partial _{alpha }J^{alpha }=0}
To put objects of the same rank in correspondence, the Laplace-Beltrami operator or Laplacian defined as:
- deployment deployment =dδ δ +δ δ d{displaystyle Box =ddelta +delta d}
We can match the four-vector current density with another object of the same range, such as the quadripotential, which carries the information of the electric potential and the magnetic vector potential.
- deployment deployment 2A=− − μ μ 0J{displaystyle Box ^{2}A=-mu _{0}J}
Or written in Lorentz coordinates we obtain that:
- ▪ ▪ μ μ ▪ ▪ μ μ Aα α =μ μ 0Jα α {displaystyle partial _{mu }partial ^{mu }A^{alpha }=mu _{0}J^{alpha }}}
Expression that reproduces the wave equations for electromagnetic potentials.
The 1-form A carries the information about the potentials of the inertial observers, its components being:
- Aα α =(≈ ≈ c,A){displaystyle A^{alpha }=left({frac {Phi }{c}}},mathbf {A} right)}
To get the geometric object that contains the fields, we need to climb the A range through the external differential operator ▪ ▪ {displaystyle partial } obtaining the 2-form F electromagnetic field. In geometric form we can write:
- F=dA{displaystyle F=mathrm {d} A}
That expressed for a Lorentz inertial system we have that:
- Fμ μ .. =▪ ▪ μ μ A.. − − ▪ ▪ .. Aμ μ {displaystyle F^{mu nu }=partial ^{mu }A^{nu }-partial ^{nu }A^{mu }}}
With which we obtain the electromagnetic field tensor.
- Fμ μ .. =[chuckles]0− − Exc− − Eandc− − EzcExc0− − BzBandEandcBz0− − BxEzc− − BandBx0]{cHFFFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cH00}{cHFFFF}{cHFFFF}{c}{c}{c}{c}{b}{c}{c}{b}{c}{c}{c}{c}{c}{c}{c}{c}{c}{c}{x}{c}{c}{c}{c}{c}{c}{c}{c}{c}{cHFFFF}{cHFFFFFF}{c}{c}{cH00}{cHFF}{c}{cH00}{cHFF}{c}{c}{c}{c}{cH00}{cHFFFF}{c}{c}{c}{cHFF}{c}{c
First pair of Maxwell's equations
The following expressions link the fields with the sources, we relate the quadcurrent with the electromagnetic field tensor through the geometric form:
- δ δ F=μ μ 0J{displaystyle ,delta F=mu _{0}J}
or in Lorentz coordinates:
- ▪ ▪ μ μ Fμ μ .. =μ μ 0J.. {displaystyle partial _{mu }F^{mu nu }=mu _{0}J^{nu }}}
Obtaining the equations
For an observable in S starting from an expression in Lorentz coordinates we can obtain:
- Stop. .. =0{displaystyle ,nu =0} We have to: ▪ ▪ μ μ Fμ μ 0=μ μ 0J0{displaystyle partial _{mu }F^{mu 0}=mu _{0}J^{0}}, then:
- μ μ 0cρ ρ (r,t)=▪ ▪ 1F10+▪ ▪ 2F20+▪ ▪ 3F30=1c[chuckles]▪ ▪ Ex▪ ▪ x+▪ ▪ Eand▪ ▪ and+▪ ▪ Ez▪ ▪ z]{displaystyle mu _{0}crho (mathbf {r}t)=partial _{1}F^{10}+partial _{2}{F^{20}{partial}{3}{F^{30}={frac}{1}{1}{left[{frac}{partial}{
Therefore:
- ► ► ⋅ ⋅ E=ρ ρ (r,t)ε ε 0{displaystyle nabla cdot mathbf {E} ={frac {rho (mathbf {r}t)}{varepsilon _{0}}}}}}}}
- Stop. .. =1,2,3{displaystyle ,nu =1,2,3} we can get in the same way as:
- ► ► ∧ ∧ H=J+▪ ▪ D▪ ▪ t{displaystyle nabla wedge mathbf {H} =mathbf {J} +{frac {partial mathbf {D}}{partial t}}}}}}}
Second pair of Maxwell's equations
They correspond to the homogeneous equations. Written in geometric form we have:
- δ δ ↓ ↓ F=0{displaystyle ,delta *F=0}
That correspond to the expression in Lorentz coordinate systems:
- ▪ ▪ μ μ ↓ ↓ Fμ μ .. =0{displaystyle ,partial _{mu }*F^{mu nu }=0}
Where the tensor ↓ ↓ F{displaystyle ,*F} is the F dual tensor. It is obtained by the Hodge operator.
Obtaining the equations
- Stop. .. =0{displaystyle ,nu =0}:
- ▪ ▪ μ μ ↓ ↓ Fμ μ 0=▪ ▪ 1↓ ↓ F10+▪ ▪ 2↓ ↓ F20+▪ ▪ 3↓ ↓ F30=[chuckles]▪ ▪ Bx▪ ▪ x+▪ ▪ Band▪ ▪ and+▪ ▪ Bz▪ ▪ z]=0{displaystyle partial _{mu }*F^{mu 0}=partial _{1}F^{10}+partial _{2}*F^{20}+partial _{3}{3}{3}}}{left[{frac {partial B_{x}}{partial x}{#
Therefore:
- ► ► ⋅ ⋅ B=0{displaystyle nabla cdot mathbf {B} =0}
- Stop. .. =1,2,3{displaystyle ,nu =1,2,3} the vector equation is obtained:
- ► ► ∧ ∧ E+▪ ▪ B▪ ▪ t=0{displaystyle nabla wedge mathbf {E} +{frac {partial mathbf {B}{partial t}}}=0}
The property ▪ ▪ α α ↓ ↓ Fα α β β =0{displaystyle ,partial _{alpha }*F^{alpha beta }=0} reproduces the inner Maxwell equations, which can be expressed as dF=0{displaystyle ,dmathbf {F} =0}, which can be written in the coordinated Lorentz systems as:
- ▪ ▪ γ γ Fα α β β +▪ ▪ β β Fγ γ α α +▪ ▪ α α Fβ β γ γ =0{displaystyle partial _{gamma }F_{alpha beta }+partial _{beta }F_{gamma alpha }+partial _{alpha }F_{beta gamma }=0}
We can summarize the set of expressions that relate the objects that describe the electromagnetic field in the following table. The first column is the geometric relations, independent of any observer; the second column are the equations described by a Lorentz coordinate system; and the third is the description of the relationship and the law that it complies with.
| Geometric form | Covariant Lorentz | Description |
|---|---|---|
| δ δ A=0{displaystyle ,delta A=0} | ▪ ▪ μ μ Aμ μ =0{displaystyle ,partial _{mu }A^{mu }=0} | Status/gauge of Lorenz (*) |
| F=dA{displaystyle ,F=dA} | Fμ μ .. =▪ ▪ μ μ A.. − − ▪ ▪ .. Aμ μ {displaystyle F^{mu nu }=partial ^{mu }A^{nu }-partial ^{nu }A^{mu }}} | Definition of Electromagnetic Fields |
| deployment deployment A=μ μ 0J{displaystyle Box A=mu _{0}J} | ▪ ▪ μ μ ▪ ▪ μ μ Aα α =μ μ 0Jα α {displaystyle partial _{mu }partial ^{mu }A^{alpha }=mu _{0}J^{alpha }}} | Ondas equations |
| δ δ F=μ μ 0Jδ δ ↓ ↓ F=0{displaystyle {begin{matrix}delta F=mu _{0}J\delta *F=0end{matrix}}}}} | ▪ ▪ μ μ Fμ μ .. =μ μ 0J.. ▪ ▪ μ μ ↓ ↓ Fμ μ .. =0{displaystyle {begin{matrix}partial _{mu }F^{mu nu }=mu _{0}J^{nu }partial _{mu }*F^{mu nu }= | Maxwell equations |
| δ δ J=0{displaystyle ,delta J=0} | ▪ ▪ α α Jα α =0{displaystyle partial _{alpha }J^{alpha }=0} | Cargo Maintenance Act |
(*) There is a common confusion regarding the nomenclature of this gauge. The first equations in which such a condition appears (1867) are due to Ludvig V. Lorenz, not the much better known Hendrik A. Lorentz. (See: J.D. Jackson: Classical Electrodynamics, 3rd edition p.294)
Finally, the quadgradient is defined like this:
- ▪ ▪ ▪ ▪ xα α =def▪ ▪ α α =def,α α =def(▪ ▪ ▪ ▪ ct,► ► ){displaystyle {mathrm {def}}{partial x^{alpha }}}{stackrel {mathrm {def}{=}}{partial _{alpha }{stackrel {mathrm {def}}}{=}{alphade }{alphade}{alphade}{
The repeated indices are summed according to the Einstein summation convention. According to tensor calculus, indices can be raised or lowered by means of the fundamental matrix g.
The first tensor is an expression of two Maxwell's equations, Gauss's law and generalized Ampère's law; the second equation is consequently an expression of the other two laws.
It has been suggested that the Lorentz force component v→ → × × B→ → {displaystyle {vec {v}}times {vec {B}}}} can be derived from the law of Coulomb and therefore the special relativity assumes the invariance of the electric charge.
Expression of the equations for a constant frequency
In Maxwell's equations, vector fields are not just position functions, they are generally position and time functions, such as for example H→ → (x,and,z,t){displaystyle {vec {H}(x,y,z,t)}. For the resolution of these equations in partial derivatives, the positional variables are found with the temporal variable. In practice, the resolution of such equations may contain a harmonic (non-usoidal) solution.
With the help of complex notation you can avoid the temporary dependence of harmonic results, thus eliminating the complex factor of expression eiω ω t{displaystyle e^{iomega t}}. Much of Maxwell's equation resolutions take complex amplitudes, as well as not only function of position. Instead of partial derivation in time you have the multiplication of the imaginary factor iω ω {displaystyle iomega }Where ω ω {displaystyle omega } is the angular frequency.
In complex form, Maxwell's equations take the following form:
- ► ► → → ⋅ ⋅ D→ → =ρ ρ {displaystyle {vec {nabla}}cdot {vec {D}}=rho }
- ► ► → → ⋅ ⋅ B→ → =0{displaystyle {vec {nabla}}cdot {vec {B}=0}
- ► ► → → × × E→ → =− − iω ω B→ → {displaystyle {vec {nabla}}times {vec {E}}=-iomega {vec {B}}}}
- ► ► → → × × H→ → =ı ı → → =(σ σ +iω ω ε ε )E→ → {displaystyle {vec {nabla}}times {vec {H}}}={vec {imath }}=(sigma +iomega varepsilon){vec {E}}}}}
Contenido relacionado
Plasma (state of matter)
Stokes's theorem
Infinitesimal





























































































![mu _0 c rho (mathbf{r},t)=part_1 F^{1 0}+part_2 F^{2 0}+part_3 F^{3 0} =
frac {1}{c} left [ frac{part E_x}{part x}+frac{part E_y}{part y}+frac{part E_z}{part z} right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0748536a35274344bc726ffdf04f4294bd1d9eb5)






![partial_mu * F^{mu 0}=partial_1 * F^{1 0}+partial_2 * F^{2 0}+partial_3 * F^{3 0}=left [ frac{part B_x}{part x}+frac{part B_y}{part y}+frac{partial B_z}{part z} right ]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f9407e838017e819dc8ccd58764f4afac6545f9)


















