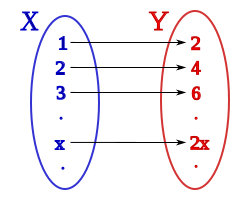Mathematical correspondence

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Given two sets: X and Y, and a function f, which determines some binary relationship between some element of X with some element of Y, we will say that this function: f, defines a correspondence between X and Y, which we will represent:

{displaystyle fcolon Xrightarrow Y}

when at least one element of X is related to at least one element of Y.

An example

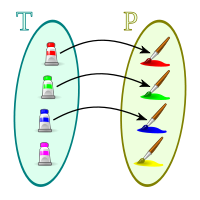
If we have a series of objects, such as paint tubes and brushes, and we differentiate tubes on the one hand and brushes on the other, and we associate each tube with the brush that has the same color of paint, we have a paint color relationship between each tube and each brush that has the same color.

In this example, we can define a set T of paint tubes and another P of brushes and associate to each tube of the set T, the brush from the set P that has the same color, we will represent this association with an arrow from the tube to the corresponding brush.

It may be the case that we have a tube of one color but not a brush with the same color of paint, as in the example there is a tube of red color but there is no brush with red paint, therefore of the red tube no arrow comes out.

We may have a tube of one color and several brushes with paint of that same color, so in the example there is a green tube and two brushes with green paint, two arrows come out of the green tube, one to each brush with paint green.

It may also be that we have more than one tube of the same color and a single brush with that paint, in this case, as in the example, the two arrows come from the two blue tubes to the only brush with blue paint, two arrows arriving at the blue brush, one from each of the blue tubes, as seen in the figure.

In the example figure you can see a brush with yellow paint, but there is no tube of yellow paint, therefore no arrow reaches this brush.

In short, the correspondence same paint color between a set T of tubes of paint, and another set P of brushes, exists as long as at least one tube of paint has the same color as one of the brushes, this relationship can be as simple or as complex as desired.

In a mathematical correspondence, sets do not necessarily have to be numeric, nor does the relationship between their elements have to be arithmetic operations, without this ceasing to be mathematical.

Definitions

In a correspondence we can distinguish different sets:

Initial: is the first of the correspondence, is this case X, we will represent it: in(f)according to the example:

{displaystyle X={rm {in}}(f)={1,2,3,4},}

In the second example, we have a correspondence between a set of brushes P and a set of faces C that we have painted with those brushes, the correspondence associates each brush the face of the same color, in this example the initial set will be:

{displaystyle P={rm {in}}(color)={,}

{displaystyle },}

Final set: is the second of the correspondence in this case And, we will represent it as fin(f)according to the example:

{displaystyle Y={rm {fin}}(f)={a,b,c,d},}

In the example of the brushes and the faces the final set is formed by:

{displaystyle C={rm {fin}}(color)={,}

{displaystyle },}

Joint origin: is formed by the elements of the initial set, which are related to some element of the final set, we will represent it or(f), in the example will be:

{displaystyle {rm {or}}(f)={2,3},}

The brushes with a painted face is the origin set, of the same color correspondence:

{displaystyle {rm {or}}(color)={,}

{displaystyle },}

Picture frame: it is formed by the elements of the final set with which the elements of the origin group are related, we will represent it Im(f)in the example:

{displaystyle {rm {Im}}(f)={c,d},}

The faces for which there is a brush of its color is the image set:

{displaystyle {rm {Im}}(color)={,}

{displaystyle },}

Homologists: two elements, one of the origin and the other of the image set, are said to be homologues, if related to correspondence f, in the example the following pairs are homologues:

{displaystyle (2,d),;(3,c)}

The ordered pairs formed by a brush and a face of the same color are:

{displaystyle (,}

{displaystyle),(,}

{displaystyle),(,}

{displaystyle),}

Image of an element: given an element x of the origin group, and another element and of the image set, it is said that and is image of x and represented:

{displaystyle f(x)=y,}

if the x element is related to the y element by the f mapping. in the example we have:

{displaystyle f(2)=d,}

{displaystyle f(3)=c,}

The color correspondence by which each brush is associated with the face painted in the same color is:

{displaystyle {rm {color}}(,}

{displaystyle)=,}

{displaystyle {rm {color}}(,}

{displaystyle)=,}

{displaystyle {rm {color}}(,}

{displaystyle)=,}

Correspondence defined from Cartesian product

Given the sets X (initial) e And (final set) and defined Cartesian product ${displaystyle Xtimes Y}$ of these two sets, like the set of pairs ordained (x, and), where ${displaystyle xin X}$ e ${displaystyle yin Y}$ , given the set F containing pairs Homon of correspondence fand ${displaystyle Fsubset (Xtimes Y)}$ define that correspondence as a whole.

Therefore we can say that a correspondence between two sets X e And It's a subset. F of the Cartesian product ${displaystyle Xtimes Y}$ which collects the pairs ordained (x, and), which form the correspondence.

Example 1

d	(1,d)	(2,d)	(3,d)	(4,d)
c	(1,c)	(2,c)	(3,c)	(4,c)
b	(1,b)	(2,b)	(3,b)	(4,b)
a	(1a)	(2a)	(3a)	(4a)
X×Y	1	2	3	4

in the diagram above, we have the sets:

{displaystyle X={1,2,3,4},}

{displaystyle Y={a,b,c,d},}

product ${displaystyle Xtimes Y}$ is:

${displaystyle Xtimes Y}$	${displaystyle ={,}$	${displaystyle (1,a),,(1,b),,(1,c),,(1,d),}$
		${displaystyle (2,a),,(2,b),,(2,c),,(2,d),}$
		${displaystyle (3,a),,(3,b),,(3,c),,(3,d),}$
		${displaystyle (4,a),,(4,b),,(4,c),,(4,d)}$	${displaystyle },}$

the set F is as follows:

{displaystyle F={(2,d),(3,c)},}

You can appreciate that ${displaystyle Fsubset (Xtimes Y)}$ and that F defines the correspondence in its entirety.

Example 2

Starting from the correspondence between the tubes of paint T, and the brushes P, associating to each tube the brush that has paint of the same color.

The correspondence will be defined by the ordered pairs:

{displaystyle F={(,}

{displaystyle),(,}

{displaystyle),(,}

{displaystyle)},}

We see that the initial set is:

{displaystyle T={,}

{displaystyle },}

and the final set:

{displaystyle P={,}

{displaystyle },}

The Cartesian product of T by P is the set of ordered pairs of each of the tubes of T with each of the brushes of P, in the grid we can see in the lower row each of the tubes of the set T, and in the left column each of the brushes of the set P, where the corresponding tube and brush intersect a row and a column, the background of the pairs that are part of the correspondence have been highlighted.

Reverse correspondence

Given a correspondence between the sets A and B, represented:

{displaystyle f:Arightarrow B}

defined as reverse correspondence fThat we'll call ${displaystyle f^{-1},}$ :

{displaystyle f^{-1}:Brightarrow A}

a which associates the image of function f with its source.

Defined a correspondence Fas a subset of Cartesian product ${displaystyle Atimes B}$ where the pairs ordered (a, b) are the associates of correspondence, inverse correspondence ${displaystyle F^{-1},}$ is the subset of the Cartesian product ${displaystyle Btimes A}$ , formed by the pairs ordered (b, a) obtained from changing the order of the correspondence F.

Thus, if we have a set T of tubes of paint and another set P of brushes and we associate by a relationship f to each tube of T the brush with paint of the same color:

{displaystyle f:Trightarrow P}

and this function is defined by the ordered pairs:

{displaystyle ,(}

{displaystyle),,(}

{displaystyle),,(}

{displaystyle),}

The inverse correspondence will be the one that starting from the set of brushes P associates to each brush the tube of the set T of paint of the same color:

{displaystyle f^{-1}:Prightarrow T}

which will be defined by the ordered pairs:

{displaystyle ,(}

{displaystyle),,(}

{displaystyle),,(}

{displaystyle),}

Types of correspondences

Given the set of all possible correspondences: C between two sets, one can distinguish:

Correspondences univores: Uif they fulfill the unique image.

Correspondences biunivores: Bif they fulfill the uniqueness of origin and image.

The applications Aif they fulfill the uniqueness and existence of image.

Applications S: Sif the uniqueness and existence of image and the existence of origin are fulfilled.

As well as the intersections of those sets.

Classification according to uniqueness

Starting from two sets, one initial X, and another final Y, and all the possible correspondences that can be made between these two sets, for its interest we can differentiate the one-to-one and one-to-one correspondences.

A correspondence is univo: U if every initial element only has an image.

Informally: "if only one arrow comes out of each element of the initial set that has an image."

A correspondence is biunivo: B if each initial element has only one image, and each image element has only that origin.

Informally: "If only an arrow comes out of the element of the initial set that has an image and such element of the final set has only that arrow that reaches an origin."

It is not necessary in any of the two cases, that all the elements of X have an image, nor that all the elements of Y have an origin, clearly an correspondence has to be one-to-one in order to be one-to-one.

If we represent with a rectangle all the possible correspondences between the sets X and Y, if the set U is the one of univocal correspondences, and at B that of the one-to-one correspondences, in a Venn Diagram, it is clearly seen that the set of one-to-one correspondences is a subset of the one-to-one correspondences.

Non-univocal correspondence

It is the correspondence in which at least one of the origin elements has two or more images. In the Venn diagram, are the correspondences that do not belong to U: U’.

If the initial set is that of the students of a school, and the final set is that of the subjects taught in that center, the correspondence of students with subjects will not be unambiguous when at least one student studies two or more subjects.

In the diagram in the figure, the element 3 has two images b and c, this means that the correspondence is not unique, regardless of the relationship that the rest of the elements have. This double image for a single origin allows us to say:

{displaystyle f(3)=b,}

{displaystyle f(3)=c,}

Both expressions being true.

Univocal correspondence

It is a correspondence where each element of the origin set corresponds to only one element of the image set.

In the Venn diagram they are the correspondences that belong to U.

Univocal correspondence, not biunivocal

It is the one that corresponds to each origin a single image, but not all images have a single origin. In the Venn diagram, are the correspondences that belong to U but not to B: U-B.

If the initial set is that of the people of a population, and the final set is that of the addresses of that population, the correspondence of people with addresses will be univocal but not biunivocal when each person lives in a single address and Several people live in a house.

The correspondence represented in this diagram is one-to-one, but it is not one-to-one because the d element has two origins: 1 and 2. Thus we have that:

{displaystyle f(1)=d,}

{displaystyle f(2)=d,}

This means that it is not a one-to-one correspondence, although for the rest of the relationships it can be.

One-to-one correspondence

It is a unique correspondence whose inverse correspondence is also unique.

That is: each element of the source set corresponds to only one element of the image set, and each element of the image set corresponds to only one element of the source set.

In the Venn diagram they are the correspondences that belong to B.

Examples

The figure diagram shows that:

{displaystyle f(2)=a,}

{displaystyle f(3)=b,}

{displaystyle f(4)=d,}

where these are all the relations of this correspondence. Source elements have a single image, and image elements have a single source, there can be non-image elements such as 1, and non-source elements such as c, but this it does not influence the definition of biuniqueness.

If we consider as an origin group that of people, and as a whole image that of cars, this correspondence will be biunivorous when people who have a car have a single car, and each car has a single owner.
A bi-unique correspondence can be established between each natural number and its square.
Another example could be a two-year correspondence between each student with their enrolment number.
A well-used and independent bi-universe relationship of other values is the one between the value of the thermometric property used and the numerical value of the assigned temperature. This is that each temperature value corresponds only to a value of the thermometer scale and each value of the thermometer scale corresponds only to a temperature value.

Math application

Main article: Mathematical function

Given a mathematical correspondence between all the elements of the set X with the elements of the set Y, we will say that this correspondence, f, is a map between X and Y when each element of X is related to a single element of And. It is also often called a mathematical function and is represented:

{displaystyle f:Xrightarrow Y}

Commonly: all the elements of the source set have an arrow and only one

That is: a mathematical correspondence is an application, if all the elements of the initial set have an image and only one image.

The diagram shows the sets X and Y:

d	(1,d)	(2,d)	(3,d)	(4,d)
c	(1,c)	(2,c)	(3,c)	(4,c)
b	(1,b)	(2,b)	(3,b)	(4,b)
a	(1a)	(2a)	(3a)	(4a)
X×Y	1	2	3	4

{displaystyle X={1,2,3,4},}

{displaystyle Y={a,b,c,d},}

As you can see, each of the X elements corresponds to a unique Y element. The a element of AND has no origin and the b element has two origins (1 and 4), but this does not affect the definition of application as a mapping type.

Types of Math Application

Given two sets X, Y, and all possible applications: A that can be formed between these two sets, one can differentiate the following cases:

If each image has a unique origin, injecting.

Vulgarmente: "to every element of the final set that has origin, only one arrow comes."

If the application is above all the final set, onyxative: S.

Vulgarmente: “If all the elements of the final set reach them an arrow, at least.”

In addition to these two characteristic cases, an application can be simultaneously injective and surjective, which are called bijective, or neither in which case it does not have a specific name.

Vulgarmente: "in a bi-ective application all the origin elements have an arrow and all the image elements, they get a single arrow."

We are going to represent the types of applications in a Venn Diagram, the universal set U, represented by a rectangle, is that of all possible applications, the set A is that of the injective applications, and the set B that of the surjectives, this allows us to see the different types of applications graphically.

Injective and non-surjective application

In an injective application each image element will have a unique origin and a non-surjective one will have at least one element of the final set that does not have an origin element.

In the Venn diagram they correspond to the applications that belong to A and do not belong to B, that is, those that belong to the difference of A and B: A-B.

In these applications, the cardinality of X is always less than that of Y, that is, the set Y will have a greater number of elements than X when we try to compare them.

Example

in the diagram of the figure:

all elements Andwhich have origin, have a single origin, this makes the application injective

element d of And, it has no origin so this application is not overyective.

Second example

Starting with the set of brushes with colored paint:

{displaystyle P={,}

{displaystyle },}

About the set of painted faces:

{displaystyle C={,}

{displaystyle },}

Associating each brush with the corresponding face:

Since each brush has one face and only one face of its color, this correspondence is an application, since the faces that a brush has of its color have only one brush of its color, the application is injective, and since the face painted yellow, it does not have any brush of this color, the application is not surjective.

Non-injective and surjective application

A non-injective map has at least one image element that has two or more origins and a surjective all elements of the final set have at least one origin element.

In the Venn diagram they correspond to the applications that do not belong to A and if they belong to B, this is the ones that belong to the difference of B and A: B-A.

For this application the set X must have a greater number of elements than Y, the cardinality of X must be greater than the of AND.

Example

in the diagram of the figure:

element c of And, has two origins: the 3 and 4, so this application is not injective.

all elements And, they have origin, this makes the application super-yective.

Second example

As in the previous example, we will start from the set of brushes with colored paint:

{displaystyle P={,}

{displaystyle },}

In this case there are two brushes with blue paint, but despite having the same color of paint, they are two different brushes.

As a final set we have the set of painted faces:

{displaystyle C={,}

{displaystyle },}

Associating each brush with the face of the same color, we see that each brush has one face painted with its color and only one, this makes the correspondence an application, the blue face has two brushes of the same color, so which is not injective, all faces have a brush with their color, so the application is surjective.

Injective and surjective application (bijective)

If an application is injective and surjective simultaneously, it is called bijective. Because it is injective, the elements that have an origin have a single origin and because it is surjective, all the elements of the final set have an origin.

In the Venn diagram, the set A is the set of injective applications and the set B is the set of surjective applications, the bijective applications, which are injective and surjective, will be the intersection of A and B.

These two circumstances result in the set X and Y having the same number of elements, the cardinality of X is the same than that of Y, this is of great importance when trying to compare two sets:

If given two sets we can find a two-and-one application among them, we can say that the two sets have the same number of elements. The cardinality of X is equal to that of And.

Example

in the diagram of the figure:

all elements Andwhich have origin, have a single origin, this makes the application injective

all elements And, they have origin, this makes the application super-yective.

If we take the set of natural numbers as the initial set:

{displaystyle X={1,2,3,...},}

and by final set that of even natural numbers:

{displaystyle Y={2,4,6,...},}

We can see that the relationship

{displaystyle f:Xrightarrow Y}

{displaystyle f:xmapsto 2x}

By which to each natural number x of X, we associate an even number 2x of Y, is fulfilled:

f: is an application, since to each of the values x of X it corresponds to a single value 2x of And.
this application is injective since each number pairs 2x of And it corresponds to a single value x of X.
and it's overyective because all pair numbers have an origin.

This allows us to affirm that there is the same number of natural numbers as there are even natural numbers, there is the paradox that the even natural numbers are a proper subset of the natural numbers, this circumstance only occurs with infinite sets.

Second example

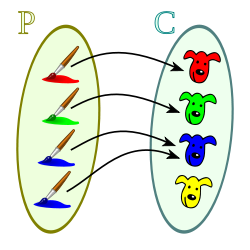
Taking the set of brushes as initial set:

{displaystyle P={,}

{displaystyle },}

and the one with faces as the final set:

{displaystyle C={,}

{displaystyle },}

The correspondence that associates each brush with the face of its same color is an application because all the brushes have a face with its color and only one face of that color, the application is injective because a brush corresponds to a single face, and it is surjective because all the faces have a brush of its color, being injective and surjective simultaneously this application is bijective.

A bijective map matches the elements of the initial set with those of the final set one by one, being able to say that there are the same number of elements in the initial set as in the final set.

Non-injective and non-surjective application

A non-injective application will have at least one image element that has two or more origins, and a non-surjective one will have at least one element of the final set that has no origin element. This type of application does not have a specific name and may be the ones that present, from a mathematical point of view, the least interest.

For this application, the sets X and Y are not comparable, and we cannot make any assumptions about their cardinality, based on their comparison, or about their number of elements.

In the Venn diagram they correspond to the applications that do not belong to A and do not belong to B, that is, those that do not belong to the union of A and B.

Example

in the diagram of the figure:

element b of AndIt has two origins: 1 and 2, this makes this application not injective

element a of And, it has no origin so this application is not overyective

Second example

If we take the initial set of colored brushes:

{displaystyle P={,}

{displaystyle },}

and as a final set the one with colored faces:

{displaystyle C={,}

{displaystyle },}

We see that all brushes have one face and only one face of the same color, so this correspondence is a mathematical application.

Since the blue face has two brushes of its color, the application is not injective, and since the yellow face does not have any brush of that color, it is not surjective, therefore this application is non-injective and not surjective.

Contenido relacionado

Más resultados...