Material fatigue

In engineering and, especially, in materials science, material fatigue refers to a phenomenon whereby materials break under cyclical dynamic loads more easily than under cyclical dynamic loads. static charges. Although it is a phenomenon that, without formal definition, was recognized since antiquity, this behavior was not of real interest until the industrial revolution, when in the middle of the century XIX began to produce the necessary forces to cause materials to break with dynamic loads much lower than those necessary in the static case and to develop calculation methods for the design of reliable parts. This is not the case for materials of recent appearance, for which it is necessary to manufacture and test prototypes.
- Denominated repeated load cycle, the maximums and minimums are asymmetrical regarding the zero load level.
- Random: the level of tension can vary randomly in amplitude and frequency.
The amplitude of the stress varies around a mean value, the average of the maximum and minimum stresses in each cycle:
- σ σ m=σ σ max+σ σ min2{displaystyle sigma _{m}={frac {sigma _{max }+sigma _{min }}{2}}}}
The stress range is the difference between maximum and minimum stress
- σ σ r=σ σ max− − σ σ min{displaystyle sigma _{r}=sigma _{max }-sigma _{min} }
The stress amplitude is half the stress range
- σ σ a=σ σ max− − σ σ min2=σ σ r2{displaystyle sigma _{a}={frac {sigma _{max }-sigma _{min }}{2}}}={frac {sigma _{r}}}{2}}}}}
The stress ratio R is the ratio between the minimum and maximum amplitudes
- R=σ σ minσ σ max{displaystyle R={frac {sigma _{min }}{sigma _{max}}}}}}
By convention, tensile stresses are positive and compressive stresses are negative. For the case of a cycle with complete load inversion, the value of R is equal to -1.
S-N curve
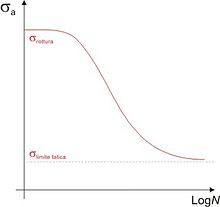
The s-n curve, also called the Wöhler curve, is obtained through a series of tests where a specimen of the material is subjected to cyclic stresses with a relatively large maximum amplitude (approximately 2/3 of static tensile strength). The cycles until failure are counted. This procedure is repeated on other specimens at decreasing maximum amplitudes.
The results are represented in a voltage diagram, Sin front of the number logarithm N from cycles to breakage for each of the specimens. Values S are normally taken as voltage amplitudes σ σ a{displaystyle sigma _{a} }.
Two types of S-N curves can be obtained. The higher the tension, the fewer number of cycles until failure. In some ferrous alloys and titanium alloys, the S-N curve becomes horizontal for large values of N, that is, there is a limit stress, called the fatigue limit, for below which fatigue failure will not occur.
It is often said, in a very superficial way, that many of the non-ferrous alloys (aluminum, copper, magnesium, etc.) do not have a fatigue limit, since the S-N curve continues to decrease with increasing N. According to this, fatigue failure will occur regardless of the magnitude of the maximum stress applied, and therefore, for these materials, the fatigue response would be specified by the fatigue resistance, which is defined as the level of stress that produces failure. after a certain number of cycles. However, this is not accurate: it is naive to believe that a material will break after so many cycles, no matter how ridiculously small the stress present.
Strictly speaking, all crystalline materials (metals,...) have a fatigue limit. It happens that for materials such as most ferrous materials, this limit is usually around one million cycles (for rotating test tube tests), for internal stresses that are around 0.7-0.45 times the elastic limit of the material; while for those that are said to have no fatigue limit, such as aluminum, it occurs even for very low stresses (in aluminum, 0.1-0.2 times said limit), and appears at very high cycles (in aluminum). aluminum can reach one billion cycles; in titanium it can be, depending on the alloy, one hundred million cycles or even, exceptionally, one trillion cycles). As in general, machines or elements are not designed so that the maximum stresses are 0.1-0.2 times the elastic limit of the material, since in that case a good part of the mechanical capacities of the material would be wasted, and neither It is usually designed assuming life values above a million cycles. In practice, this type of material will not be able to present its fatigue limit, although it does.
This confusion arises from the very nature of Wöhler S-N curves, which were devised in the 19th century for the steels. By expanding the type of metallic materials usual in engineering, the same concepts and the same curves were transferred to other metals whose fatigue behavior is essentially different (in fact, the great variability of behaviors that it presents in materials is a characteristic of fatigue itself). different types of materials). And since steel has been and is the cornerstone of engineering, it was interesting to compare the properties of other metals with respect to it: it is and was common that, when testing materials, the tests were suspended once they exceeded a million cycles, considering that it was not interesting to characterize materials beyond that time limit.
Another important parameter that characterizes the fatigue behavior of a material is the fatigue life Nf. It is the number of cycles to produce a failure at a specified stress level.
In addition, knowledge of fatigue behavior is not the same for all materials: the best-known, most tested, and most reliable material in terms of fatigue predictions is the family of steels. Less information is available on other commonly used metallic materials such as aluminum, titanium, copper, nickel, magnesium or chromium alloys (this decreases with the newness of the alloy), although the form of the fatigue calculation criteria and from the S-N curves it appears regular, and is similar to that of steels, and its reliability is considered to be high. For ceramic materials, on the contrary, very little information is available, and in fact, the study of fatigue in them and in polymers and composite materials is a hot topic of current research.
In any case, there is a notable difference between theory and reality. This leads to significant design uncertainties when fatigue life or fatigue limit are considered. The scatter in the results is a consequence of the sensitivity of fatigue to various test and material parameters that are impossible to control precisely. These parameters include specimen fabrication and surface preparation, metallurgical variables, alignment of the specimen in the testing equipment, mean stress, and frequency of test loading.
Approximately half of the specimens tested fail at stress levels that are about 25% below the curve. This is usually associated with the presence of internal stress concentration sources, such as defects, impurities, notches, scratches,..., which have remained undetected.
Statistical techniques have been developed and used to handle this failure in terms of probabilities. A convenient way to present the results treated in this way is with a series of constant probability curves.
| Fatigue | Cycles |
|---|---|
| Low number of cycles (oligofatiga) | . 103 - 105 |
| High number of cycles | ▪ 103 - 105 |
Crack initiation and propagation
The fatigue failure process develops from the beginning of the crack and continues with its propagation and final failure.
Home
Cracks that cause rupture or fracture almost always nucleate on the surface at a point where stress concentrations (caused by design) exist.Cyclic loading can produce microscopic surface discontinuities from steps produced by dislocation slip, which will act as stress concentrators and, therefore, as crack nucleation sites.
Propagation
- Stage I: once a crack is nucleated, then it spreads very slowly and, in polycrystalline metals, along crystallographic planes of high clutch tension; the cracks usually spread in few grains at this stage.
- Stage II: the speed of extension of the crack increases in a vertiginous way and at this point the crack stops growing in the axis of the effort applied to start growing in the direction perpendicular to the applied effort. The crack grows by a process of enrolment and sharpening of the tip because of the tension cycles.
Break
As the crack increases in width, the end is advanced by continuous shearing until it reaches a blunt configuration. A critical crack dimension is reached and failure occurs.
The region of a fracture surface that formed during stage II propagation can be characterized by two types of marks, called beach marks and striations. Both indicate the position of the crack end at different instants and have the appearance of concentric ridges expanding from the initiation points. Beach tags are macroscopic and can be seen with the naked eye.
Beach marks and ridges do not appear in fast breaks.
Speed of propagation
The results of fatigue studies have shown that the life of a structural component can be related to the rate of crack growth. The rate of crack propagation is a function of the stress level and the amplitude of the crack.
| Symbol | Name | Unit |
|---|---|---|
| C | Constant for a given material | |
| m | Constant for a certain material (between 1 and 6) | |
| K | Stress intensity factor | |
| da / dN | Earring of Growth Speed Curve |
- Δ Δ K=Kmax− − Kmin{displaystyle Delta K=K_{max }-K_{min }}
or else
- Δ Δ K=AndΔ Δ σ σ π π a{displaystyle Delta K=YDelta sigma {sqrt {pi a}}}}
Developing these expressions from graphs generated by themselves, it is possible to arrive at the following equation:
| Symbol | Name | Unit |
|---|---|---|
| Nf | Number of cycles to breakage | |
| And | Independent parameter of the length of the crack | |
| m | Constant for a given material | |
| C | Constant for a given material | |
| ac | Critical length of the crack | |
| a0 | Initial crack length |
| Symbol | Name | Unit |
|---|---|---|
| K1c | Tenacity of fracture of flat deformations |
These formulas were generated by Paul C. Paris in 1961 by making a log-log plot of crack growth rate against stress intensity factor showing a linear relationship on the plot. Using this graph, quantitative predictions can be made about the residual life of a specimen given a particular crack size. This is the beginning of the initiation or rapid crack initiation.
Factors involved
There are various factors involved in a fatigue failure process apart from the applied stresses. Thus, design, surface treatment and surface hardening may be of relative importance.
Design
Design has a large influence on fatigue failure. Any geometric discontinuity acts as a stress concentrator and is where the fatigue crack can nucleate. The sharper the discontinuity, the more severe the stress concentration.
The probability of failure due to fatigue can be reduced by avoiding these structural irregularities, that is, making modifications to the design, eliminating abrupt changes in the contour that lead to sharp edges, for example, requiring rounded surfaces with larger radii of curvature.
The dimensions of the piece also influence, increasing its size we obtain a reduction in the fatigue limit.
Surface treatments
In machining operations, small scratches and grooves are produced on the surface of the piece by cutting action. These marks limit the fatigue life as they are small cracks which are much easier to enlarge. Improving the surface finish by polishing increases the fatigue life.
One of the most effective methods of increasing yield is by compressive residual stress within a thin surface layer. Any external tensile stress is partially offset and reduced in magnitude by the compressive residual stress. The net effect is that the probability of crack nucleation, and hence fatigue failure, is reduced.
This process is called “shot blasting” or “shot blasting”. Small, hard particles with diameters in the range of 0.1 to 1.0 mm are projected at high speeds onto the surface to be treated. This deformation induces compressive residual stresses.
Surface Hardening
It is a technique by which both the surface hardness and the fatigue life of alloy steels are increased. This is accomplished by carburizing and nitriding processes, in which a component is exposed to a carbon-rich or nitrogen-rich atmosphere at elevated temperatures. A carbon-rich surface layer in nitrogen is introduced by atomic diffusion from the gas phase. This layer is normally 1mm deep and is harder than the core material. The improvement in fatigue properties comes from the increase in hardness within the layer, as well as from the residual compressive stresses that originate in the cementation and nitriding process.
Influence of the environment
The environment can affect the fatigue behavior of materials. There are two types of media fatigue: thermal fatigue and corrosion fatigue.
Thermal fatigue
Thermal fatigue is normally induced at elevated temperatures due to fluctuating thermal stresses; mechanical stresses of external origin need not be present. The cause of these thermal stresses is the restriction to expansion and/or contraction that normally occur in structural parts subjected to temperature variations. The magnitude of the resulting thermal stress due to a change in temperature depends on the coefficient of thermal expansion and the modulus of elasticity.
Static fatigue (corrosion-fatigue)
Corrosion fatigue occurs due to the action of cyclic stress and simultaneous chemical attack. Logically corrosive media have a negative influence and reduce fatigue life, even the normal atmosphere affects some materials. As a consequence, small fissures or pits can be produced that will behave as stress concentrators, causing cracks. Propagation is also increased in the corrosive medium since the corrosive medium will also corrode the interior of the crack producing new stress concentrators.
Contenido relacionado
Wire
Electronics
C++