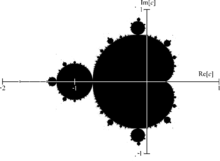
Mandelbrot set
The Mandelbrot set is the most studied fractal. It is thus known in honor of the mathematician Benoît Mandelbrot (1924-2010), who did research on it in the 1970s.
This set is defined in the complex plane by fixing any complex number c. From c, a sequence is constructed by recursion:
{z0=0한 한 C(initial term)zn+1=zn2+c(recursive succession){displaystyle {begin{cases}z_{0}=0in mathbb {C} &{text{(initial term)}}qquad \z_{n+1}=z_{n}{n}^{2}+c stranger{text{(recursive succession)}}}end{cases}}}
If this sequence is bounded, then c is said to belong to the Mandelbrot set, and if not, it is excluded from it.
For example, if c = 1 we obtain the sequence 0, 1, 2, 5, 26, …, which diverges. Since it is not bounded, 1 is not an element of the Mandelbrot set.
On the other hand, if c = –1 we obtain the sequence 0, –1, 0, –1, …, which is bounded and, therefore, –1 does belong to the Mandelbrot set.
The array is often represented using the escape time algorithm. In this case, the colors of the points that do not belong to the set indicate the speed with which the sequence corresponding to said point diverges (tends to infinity, in module). In the example image, we can see that dark red indicates that after a few calculations it is known that the point is not in the set, while white indicates that it took much longer to verify it. Since an infinite number of values cannot be calculated, it is necessary to set a limit and decide that if the first p terms of the sequence are bounded, then the point is considered to belong to the set. Increasing the value of p improves the accuracy of the image.
On the other hand, it is known that the points whose distance to origin is greater than 2, that is,
4}" xmlns="http://www.w3.org/1998/Math/MathML">x2+and2▪4{displaystyle x^{2}+y^{2}{2}4}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/78a88be1c49b5b1104b2249e6f54e88a623eca3b" style="vertical-align: -0.671ex; width:11.7ex; height:3.009ex;"/> They don't belong to the whole. Therefore it is enough to find a single term of succession that verifies 2}" xmlns="http://www.w3.org/1998/Math/MathML">日本語zn日本語▪2{displaystyle Δz_{n} Ministère2}
2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0798b8a1c835d8b3f8c2680eec91c247d84b3a36" style="vertical-align: -0.838ex; width:7.854ex; height:2.843ex;"/> to be sure that c It's not on the whole.
Invariance at various scales
A fundamental property of fractals is the total or partial invariance of certain characteristics in relation to different scales, in particular, when enlarging certain parts of a fractal image, an image similar to the initial one reappears and so on. Below are enlargements of the main image:
Green Box
Grey mini box
White box
By enlarging the green box, you can see:
- One can see Ball black with a contour very similar to the initial image.
- Next Ball wide black of the green box is more similar to the larger than the initial image.
By enlarging the gray box located on the far left of the initial image, its resemblance to the initial image is obvious. The process can be repeated an endless number of times by choosing the image to be enlarged well.
By enlarging the purple box of the main image, the image appears as a spot on the top left that apparently has the same shape as the initial image.
Violet box
Detail of the violet box
Detail
Now, let's enlarge the light blue box to the right of the plan (right image):
Let's zoom in on the white box in the last image (on the left): Here a slight deformation of the initial figure is noticeable. However, this image is still isomorphic to the initial one. And of course, around each clone of the initial shape there are other tiny clones, in the same relative positions as in the global figure. The process has no end.
- Other representation
In this image, the set is naturally the same, but the level lines (that separate the colors, outside the set) are not identical. This is because the same criterion of divergence has not been used, in this image it is really 2}" xmlns="http://www.w3.org/1998/Math/MathML">日本語zn日本語▪2{displaystyle Δz_{n} Ministère2}2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0798b8a1c835d8b3f8c2680eec91c247d84b3a36" style="vertical-align: -0.838ex; width:7.854ex; height:2.843ex;"/>while in the previous era 10}" xmlns="http://www.w3.org/1998/Math/MathML">日本語zn日本語▪10{displaystyle UDIz_{n}SUBMIT10}
10}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/95a463f2a7f8a7fdbda4d3729b0d54d8eb8417a5" style="vertical-align: -0.838ex; width:9.017ex; height:2.843ex;"/>, for aesthetic reasons, since so you get an initial image less dark.
History
The basic theory on the iteration of complex functions was developed by Gaston Julia and Pierre Fatou in the 1910s. The extraordinarily intricate shape of sets related to these iterations was revealed by the time computer graphics was advanced enough. The first somewhat crude images of the set by Robert Brooks and Peter Matelski date from 1978.
Benoit Mandelbrot studied the parameter space of quadratic polynomials in a paper that appeared in 1980 and sparked global interest in it.
The rigorous mathematical study of this set really began with the work of mathematicians Adrien Douady and John H. Hubbard, who demonstrated many of its fundamental properties and named the set after Mandelbrot. Among other properties, they proved that it is a connected set and formulated the MLC conjecture, which formulates the belief that the Mandelbrot set is locally connected.
Relationship with the sets of Gaston Julia
There is another way to define this set: it is the complex set c for which the whole of Julia associated with fc(z)=z2+c{displaystyle f_{c}(z)=z^{2}+c} is related.
Images calculated with a digital computer
It was not until the first digital computers appeared that this fractal could be visualized in all its complexity.
In the series detailed below we can see how the definition of the fractal improves as we increase the number of iterations. The points that converge to a certain value appear pale yellow, and properly belong to the Mandelbrot set. The points that diverge to infinity have been colored with a chromatic range that goes from gray to black, depending on the number of iterations required (escape velocity algorithm). The fewer iterations it takes to diverge to infinity, the darker color is applied.
10 iterations by pixel
12 iterations by pixel
15 iterations by pixel
20 iterations by pixel
50 iterations by pixel
500 iterations by pixel
Properties
Topological Properties
The Mandelbrot set is compact, related and its complement is also related. Its interior, like any interior of a subset of C{displaystyle mathbb {C} } not empty, it turns out to be of the cardinality of R{displaystyle mathbb {R} }, this is a direct consequence of the usual topology C{displaystyle mathbb {C} } has an open base of non-numberable cardinality = 2Русский Русский 0{displaystyle 2^{aleph _{0}}}}.
Its border has a topological dimension of 1 but a Hausdorff dimension of 2, the maximum possible as it is a subset of the plane.
Contenido relacionado
Hamming distance
Total preorder
Diameter