Magnetochemistry
Magnetochemistry is the branch of chemistry dedicated to the synthesis and study of substances with interesting magnetic properties. Molecular magnetism, understood as a field of study and not as a phenomenon, is the part of magnetochemistry and solid state physics that deals with molecular systems. Magnetochemistry and molecular magnetism combine experimental measurements such as magnetometry with model Hamiltonians to rationalize the magnetic properties of different systems, seeking an approximation to their electronic structures in the case of ions or molecules, or to their bands in the case of extended solids.
Historical evolution
The field of interest and study of magnetochemistry has evolved over time. Historically, only compounds with magnetic ordering exhibited phenomena strong enough to be conspicuous. Therefore, the first magnetically interesting compounds were typically inorganic solids, metals like iron, or metal oxides like magnetite, to which it is difficult to make controlled chemical modifications.
At the end of the 18th century and beginning of the 19th century, studies prior to the beginning of magnetochemistry as such were limited to study of the effects of magnetic fields on chemical reactions, analogous to electrochemistry (or, bridging the gap, thermochemistry and photochemistry). The beginning of magnetochemistry as it is known today is considered to have taken place around 1905 by the French physicist Paul Langevin, who developed a microscopic model to explain diamagnetism and paramagnetism that is still studied today, while the German chemist Wilhelm Klemm was instrumental in completing the foundations of the discipline.
The development of physical methods to obtain precise magnetic information, either thermodynamic, such as the magnetometer —with Gouy's balance at the beginning of the century XX—well spectroscopic as electron spin resonance, already in the middle of the century, was crucial for the progress of the discipline. Also at the beginning of the XX century, measurements were made on diamagnetic compounds that allowed the preparation of Pascal's tables, which still they are occasionally used to correct measures of susceptibility. From a theoretical point of view, the Hamiltonian Heisenberg-Dirac-van Vleck trade-off model and the van Vleck equation were developed. These are two fundamental tools for rationalizing the properties of simple paramagnets. The first one introduces the magnetic exchange as a parameter, whose sign defines the ferromagnetic or antiferromagnetic character of the interaction and whose absolute value is directly proportional to the energy difference between the different magnetic levels. The second allows to calculate the magnetic susceptibility for any temperature in a simple way if the energy differences and the value of the magnetic moment of the different magnetic levels are known. The progressive advance in the understanding of quantum mechanics allowed the development of predictive models, such as the Goodenough-Kanamori rules that relate the character of the magnetic interaction depending on the filling of the participating orbitals.
A scientist credited with leading the way in the evolution of the discipline from magnetochemistry to molecular magnetism during the last decades of the century XX was Olivier Kahn, to the point that there is a biannual medal dedicated to young scientists dedicated to his memory, awarded by Magmanet, a network of European research groups. In Hispanic culture, the contributions to the study of paramagnetism by Blas Cabrera, at the beginning of the XX century.
Unit system
To properly read the literature in the field of magnetochemistry, especially the less recent works, it is important to take into account certain differences between the conventions of this discipline and the international system (SI), which makes it advisable to check the formulas with a careful dimensional analysis. In particular, historically different versions of the cegesimal system have been mixed with the SI, so that for example in some formulas the permeability of the vacuum is omitted, which in the SI has the value
- μ μ 0=4π π × × 10− − 7{displaystyle mu _{0}=4pi times 10^{-7}}kg s-2A-2
while in cegesimal it is the unit, maintaining the same physical magnitudes. One case in which this creates particular confusion is the definition of magnetization, which can be presented in cegesimal as
- B→ → =H→ → +M→ → {displaystyle {vec {B}}={vec {H}}}+{vec {M}}}}}
The permeability omitted in the formula may be multiplying only to H→ → {displaystyle scriptstyle {vec {H}}}} - so that B→ → {displaystyle scriptstyle {vec {B}}}} and M→ → {displaystyle scriptstyle {vec {M}}}}) are similar magnitudes—or (H→ → +M→ → {displaystyle scriptstyle {vec {H}}+scriptstyle {vec {M}}) — so that H→ → {displaystyle scriptstyle {vec {H}}}} and M→ → {displaystyle scriptstyle {vec {M}}}} are similar quantities—and different groups have used different conventions. For the same reason, the confusion between Gauss, the unity of magnetic flow density is common. B→ → {displaystyle scriptstyle {vec {B}}}} and Oersted, the ancient unit of magnetic field intensity H→ → {displaystyle scriptstyle {vec {H}}}}.
Diamagnetism
The phenomenon of diamagnetism is ubiquitous in magnetochemistry: all materials experience a diamagnetic contribution, regardless of whether or not other phenomena that may dominate their magnetic behavior take place. This derives directly from the fact that all pairs of electrons with opposite spins contribute weakly to diamagnetism, and the vast majority of electrons in all elements and compounds couple in pairs by the Pauli exclusion principle. In this way, the pairs of electrons subjected to an external field move in such a way that the magnetic field they generate opposes that external field. This decreases the magnetization within the material and generates an energetic destabilization that depends on the intensity of the field, or, in practice, a repulsion in front of areas with strong magnetic fields.
This behavior is known as diamagnetism, a phenomenon similar to that of dielectrics when faced with an electric field. For example, pure water is diamagnetic, as are nitrogen in the air and common salt. Diamagnetism generally becomes a mere minor correction when there are electronic magnetic moments in the material, whose interaction with the magnetic field is much stronger, as explained below.
Magnetic susceptibility
Excepting diamagnetism, the phenomena studied by magnetochemistry are generally due to the existence of unpaired electrons, for example in transition metals, organic radicals or rare earths. All electrons have a spin magnetic moment, the which is an intrinsic property, as fundamental of elementary particles as mass or electric charge. Normally, these moments cancel in pairs, since each orbital contains a pair of electrons with moments of opposite sign, due to the Pauli exclusion principle, which prevents them from having the same spin quantum number. When at least one electron in an atom, ion, or molecule is unpaired, the resulting material is magnetic. We speak of transition ions dn or rare earths fn to refer to the number n of electrons that are housed in their magnetic orbitals.
In the presence of a magnetic field, all magnetic systems experience the Zeeman effect, a doubling of magnetic energy levels by interaction with an external applied field. This interaction with the magnetic field results in an increase in the magnetization within the sample, and in an attraction by a magnetic field gradient, something that is quantified experimentally as magnetic susceptibility, for example with a Gouy balance or with a magnetometer of SQUID type.
This magnetic susceptibility, analogous to electrical susceptibility, is defined as
- χ χ =▪ ▪ M▪ ▪ H{displaystyle chi ={frac {partial M}{partial H}}}}
Where M is the magnetization of the material (the intensity of the magnetic moment per volume unit) and H is the intensity of the applied external magnetic field. It is experiential to determine volumomic susceptibility from apparent weight gain Δ Δ m⋅ ⋅ g{displaystyle Delta mcdot g} of an area sample A being in the presence of a magnetic field of intensity H:
- χ χ v=Δ Δ m⋅ ⋅ g⋅ ⋅ − − 2H2A{displaystyle chi _{v}=Delta mcdot gcdot {frac {frac {-2}{H^{2}A}}}}}
In the study of a magnetic system, it is common to represent the magnetic susceptibility, its inverse or the result of its multiplication by the temperature, against the temperature. Frequently, it is possible to fit some of these data to simplified laws such as the Curie or Curie-Weiss law.
Isolated spin and paramagnetism
Insulated spin paramagnetism is a fundamental piece of magnetochemistry. Being well known, it is not a prominent subject in academic research; however, this good understanding is a useful tool in the characterization of novel paramagnetic systems. Furthermore, part of the study of many magnetically complex systems is based on reductions or derivations, at least in part, from ideal paramagnetic systems.
A material is called a paramagnet when its unpaired electrons are effectively independent of each other. Their magnetic moments then progressively align with strong fields, and spontaneously disorder as field strength decreases or temperature increases, in a thermodynamic competition between energy and entropy. At low fields and high temperatures, the magnetization in these materials roughly follows Curie's law, that is, it is proportional to the field and inversely proportional to the temperature. Somewhat more generally, the magnetization of a perfect paramagnet follows a more complicated mathematical expression, Brillouin's law; As explained below, in the presence of interactions these laws undergo modifications or have to be completely discarded.
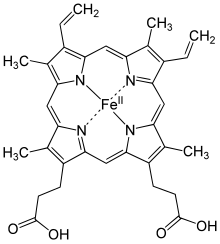
Compared to diamagnetic systems, paramagnetism has effects on magnetic susceptibility that are several orders of magnitude stronger on the energy and magnetization of the system. They are paramagnetic, for example, the oxygen in the air, the hemoglobin molecule in the blood —because of the iron ion it contains— and, for short periods of time, various products and reaction intermediates of combustion, which are free radicals.
Interactions within the same atom or ion
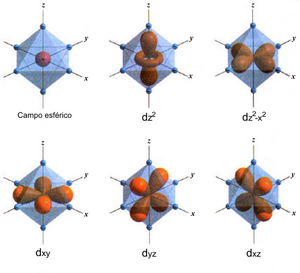
Although isolated spins are of fundamental conceptual importance, few systems of interest to magnetochemistry in particular and few actual magnetic compounds in general are so simple. For the properties of transition metal ions, for example, the number, arrangement and character of their ligands are decisive, that is, the anions or molecules that surround them, providing electron density to stabilize their positive charges. The symmetry in which the ligands are arranged determines the maximum degeneracy of the ground state. In this aspect, the octahedral coordination is of great importance, because it is typical and because almost all those commonly found are derived from it. Depending on their character, the ligands can exert either a strong or a weak field, which is crucial when there are two states close in energy that differ in the value of the magnetic moment, known as high spin and low spin states. When it is also possible to go from one to the other due to changes in pressure or temperature, or by radiation illumination (LIESST effect) of a certain wavelength. In these cases, we speak of spin equilibrium, and macroscopically it translates into a system with two possible magnetic phases, which commonly will also have slightly different crystalline structures.
The interaction between the electrons in the valence shell of the same atom or ion results in an electronic configuration, which is usually described by a spectroscopic term. If in addition to unpaired electrons there is orbital degeneracy, commonly the spin magnetic moment couples with the orbital magnetic moment. Perturbation theory is used in this as in many other points of magnetochemistry to describe complicated quantum systems in terms of simpler ones: if this interaction between spin and orbit happens in first order (directly), we speak of spin coupling. -orbit; often the Russell-Saunders coupling scheme is applicable, in which the total spin and orbit moments are still appropriate quantum numbers to describe the system. On the other hand, if the coupling is of the second order (indirect), this results in a splitting to a null field, an energy difference between magnetic levels, in the absence of an external magnetic field. Typical examples of these phenomena are found in octahedral complexes of Co(II), in the first order, in the majority of trivalent lanthanides, also in the first order and more intense, or Ni(II), in the second order, much weaker.. Both in one case and in the other, the effects on the magnetic properties are easily quantifiable, and in general the behavior is qualitatively different from that of a system with long-range order. The Landé factor is used to effectively relate the magnetic moment (and derived magnitudes) of systems having angular momentum and spin momentum, compared to the magnetic moment of a pure spin. The fact that first-order effects do not occur more frequently is due to the low molecular symmetry of most metal complexes, which breaks the orbital degeneracy and therefore eliminates the orbital magnetic moment.
In cases where there are several degenerate and not equally occupied energy levels, the Jahn-Teller theorem predicts that the system will undergo structural distortion—lengthening of some bonds and shortening of others—so that some of these levels will stabilize and others will destabilize, with a net gain in energy. This effect, of magnetic origin, has consequences on the structure and chemical reactivity of, for example, many Cu(II) complexes. The theorem, however, does not predict the magnitude of this distortion, which in some electronic configurations tends to be very slight and have hardly any practical effect.
When there are energy levels relatively close to the fundamental and therefore mixes between levels take place, it is possible to find the so-called temperature-independent paramagnetism, a magnetic moment that does not depend on the relative occupancy of the electronic levels and therefore does not vary with temperature. This phenomenon only depends on the energy and the magnetic moment of the excited states, so it can occur in systems whose fundamental state has all the paired electrons. In magnetometry, its magnitude can be comparable to or greater than the diamagnetic correction, but opposite in sign.
Magnetic interaction between centers
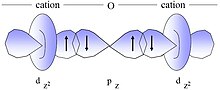
Much of the richness of magnetochemistry is due to the interaction between magnetic centers. Among these, stands out the variety of phenomena that are collectively described as magnetic exchange and that determine the alignment between the magnetic moments of neighboring atoms by a direct overlap between their orbitals (or, in the case of magnetic super exchange, through a bridging ligand). Depending on whether the resulting magnetic moment is the sum or the difference of the interacting moments, we speak, respectively, of ferromagnetic or antiferromagnetic interaction. The figure shows a simple representation of antiferromagnetic superexchange, in which the magnetic moments of the cations are arranged antiparallel, due to the partial polarization of the bridging ligand.
Usually, if the exchange does not extend to two or three dimensions, this still results in a macroscopic behavior very similar to what a paramagnet with the spin resulting from this interaction would show: two Cu(II) ions in an octahedral environment, of spin S=1/2, if they are strongly ferromagnetically coupled, they will behave very similarly to a single Ni(II) cation in an octahedral environment, of spin S=1.
In some cases, this interaction extends to several centers, giving rise to polynuclear magnetic complexes. In certain cases this gives rise to fundamentally different behaviours, for example with very high nuclearity (many magnetic centers) it is possible to find superparamagnets, whose magnetization cannot follow rapid changes in the applied external field; Some cases with high magnetic anisotropy—magnetic exchange or susceptibility of different intensity for different directions in space—are called monomolecular magnets or magnet molecules: molecules that in some respects behave like a magnet.
In the so-called mixed valence compounds, electronic transfer, the jump of an electron from one atom to another, is also of fundamental importance. Depending on the number of electrons and magnetic orbitals, electron transfer can favor ferromagnetic or antiferromagnetic interactions. When it coexists with the magnetic exchange, it is usual that the electronic transfer is the one that predominates.
On the other hand, and although it can commonly be neglected as a minor influence, in many cases the dipole magnetic interaction —such as the one that occurs between macroscopic magnets— between the individual spins is relevant. As a general rule, this interaction will be more important the greater the magnetic moments involved.
Magnetic ordering, ferromagnets and ferrimagnets
On a practical level, magnetochemistry owes much of its importance to systems where interactions are not limited to a small number of centers. In some inorganic solids —typically metallic oxides— the magnetic moments of these electrons are coupled, this coupling propagates three-dimensionally, and a magnetic ordering is reached: a large number of magnetic moments are aligned, in a solid. The Curie-Weiss law gives an approximate description of this phenomenon under certain conditions, in contrast to the Curie law that describes isolated magnetic moments.
A material is called ferromagnet if its unpaired electrons couple to point in the same direction, forming regions with high magnetic moment called magnetic domains. Ferromagnets are the conceptually simplest origin of magnets: systems that are attracted or repelled by other magnets, depending on how their magnetic poles face, and that retain a remnant magnetization after removal of the applied magnetic field, called magnetic hysteresis.
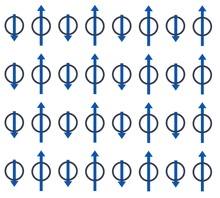
Even an antiferromagnetic coupling between two sublattices of different magnetic moment that do not completely cancel results in magnetic domains; These are systems, physically similar to those of the previous case, called ferrimagnets. Indeed, ferrimagnets are also magnets and despite their disparate origin their properties at first glance are almost indistinguishable from those of ferromagnets. In the figure we see a simplified scheme, in which the interactions in each line are antiferromagnetic, but the odd columns do not compensate the magnetic moment of the even columns. All permanent magnets—that is, all magnets that aren't electromagnets—from bits on hard drives to fridge magnets to compasses and key components in headphones and speakers are ferromagnetically or ferrimagnetically ordered substances..
In recent decades, compounds with a ferromagnetic or ferrimagnetic order have been synthesized that are partially or entirely organic, taking advantage of free radicals, such as the nitronyl nitroxide radical, in which a resonance stabilization occurs between two neighboring nitroxide groups, or triphenyl alkyl, in which access to the unpaired electron residing in an alkyl radical is blocked by the steric hindrance of three phenyl groups. In the same period also coordination chemistry has produced molecular-based magnets, magnets built from many molecules, with strong magnetic interaction but weak chemical interaction. In general, these studies are only of academic interest for now, and the applications for everyday life are future or speculative.
Without having an ordering, spin glasses are paramagnetic solids with great disorder in their magnetic structure capable of presenting some similarities with ferromagnets and superparamagnets. Another non-ordering cooperative phenomenon is the spin transition: small volume changes in a system that is in spin equilibrium sometimes influence neighboring ions so that it is possible to observe hysteresis in magnetic moment versus temperature or the pressure.
Recent Research
Currently, compounds of magnetochemical interest cover a wide range of fields, and their study overlaps with various disciplines, from solid-state chemistry to biochemistry. Recent experimental research in this field includes the search for new materials with interesting magnetic properties, or combinations of properties, for example magnetic and electrical or magnetic and optical. Thus, molecular magnets (such as Mn12) have been obtained, electrically conductive molecular-based ferromagnets, electrically superconducting paramagnets, or systems whose magnetic properties can be altered by light.
Experimental studies require novel synthesis techniques as well as sophisticated measurement devices such as SQUID-equipped magnetometers, inelastic neutron scattering, high-field electron paramagnetic resonance, spin echoes, or muon spectroscopy.
For its part, theoretical research, which includes the development and refinement of model Hamiltonians that describe magnetic exchange or electron transfer (in mixed valence compounds), continues to search for magnetostructural correlations, or correspondences between molecular (or crystalline) structure) and magnetic interactions. These increasingly sophisticated models typically require the use of quantum mechanical tools and the help of computational chemistry.
Additional bibliography
Magnetochemistry
Contenido relacionado
Ruthenium
Propane
Force