Magnetic field

ImprimirCitar

The shape of the magnetic field produced by a horseshoe magnet is revealed by the orientation of the iron rims sprayed on a sheet of paper on the magnet.

Comparison of

B

H

and

M

inside and outside a cylindrical magnetic bar.

A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any point is specified by two values, the direction and the magnitude; such that it is a vector field. Specifically, the magnetic field is an axial vector, as are mechanical moments and rotational fields. The magnetic field is most commonly defined in terms of the Lorentz force exerted on electric charges.

The term is used for two distinct but closely related fields, indicated by the symbols B and H, where, in the International System of Units, H is measured in units of amps per meter and B is measured in teslas or newtons divided by meters per amp. In a vacuum, H and B are the same thing apart from the units; but in a material with magnetization (denoted by the symbol M), B is solenoidal (has no divergence in its spatial dependence) while H it is non-rotational (free of ripples).

Magnetic fields are produced by any electric charge produced by moving electrons and the intrinsic magnetic moment of elementary particles associated with a fundamental quantum property, their spin. In special relativity, electric and magnetic fields are two interrelated aspects of an object, called the electromagnetic tensor. Magnetic forces give information about the charge carried by a material through the Hall effect. The interaction of magnetic fields in electrical devices such as transformers is studied in the discipline of magnetic circuits.

Magnetic fields are used in all modern technology, especially in electrical and electromechanical engineering. Rotating magnetic fields are used in both electric motors and generators. The interaction of magnetic fields in electrical devices such as transformers is conceptualized and investigated as a magnetic circuit. Magnetic forces give information about the charge carriers in a material through the Hall effect. Earth produces its own magnetic field, which shields Earth's ozone layer from the solar wind and is important in compass navigation.

Lorentz force

Among the definitions of magnetic field is the given by the force of Lorentz. This would be the effect generated by an electric current or magnet on a region of space in which a punctual electric charge of value (q)which moves at a speed ${mathbf {(v)}}$ experiences the effects of a force that is dry and proportional to both speed (v) like the field (B). Thus, such burden shall perceive a force described with the following equation:

${displaystyle mathbf {F} =q(mathbf {v} times mathbf {B})}$

Where F is the magnetic force, v is the velocity and B the magnetic field, also called magnetic induction and magnetic flux density. (Note that both F and v and B are vector magnitudes and the cross product results in a perpendicular vector both v and B). The magnitude of the resultant force will be:

$|{mathbf {F}}|=|q||{mathbf {v}}||{mathbf {B}}|cdot {mathop {operatorname{sen} }}(theta)$

The existence of a magnetic field is revealed thanks to the property of orienting a magnetometer (magnetized steel sheet that can rotate freely). The needle of a compass, which shows the existence of the earth's magnetic field, can be considered a magnetometer. Lorentz's law establishes that a charged particle q moving at a speed v→ through a point where there is a magnetic field intensity B→, will suffer the action of a force F→ called Lorentz force whose value is proportional to the value of q, B→ and v→ is obtained by means of the following expression:

History

Although some magnetic materials have been known since antiquity, such as the power of attraction that magnetite exerts on iron, it was not until the 19th century that the relationship between electricity and magnetism was established, passing both fields to be differentiated to form the body of what is known as electromagnetism.

Hans Christian Ørsted, Der Geist in der Natur, 1854

Before 1820, the only known magnetism was that of iron. This changed with a little-known science professor at the University of Copenhagen, Denmark, Hans Christian Oersted. In 1820 Oersted prepared in his house a scientific demonstration for his friends and students. He planned to demonstrate the heating of a wire by an electric current and also to carry out demonstrations on magnetism, for which he had a compass needle mounted on a wooden base.

While conducting his electrical demonstration, Oersted noticed to his surprise that every time the electrical current was turned on, the compass needle moved. He shut up and ended the demos, but in the following months he worked hard trying to explain the new phenomenon. But he couldn't! The needle was neither attracted nor repelled by the current. Instead it tended to stay square. Today we know that this is reliable proof of the intrinsic relationship between the magnetic field and the electric field reflected in Maxwell's equations.

As an example to see the slightly different nature of the magnetic field, just consider the attempt to separate the pole of a magnet. Even if we break a magnet in half, it "reproduces" its two poles. If we now split again in two, we will once again have each piece with the north and south poles differentiated. In magnetism magnetic monopoles have not been observed.

Name

The force on an electric charge depends on its location, speed, and direction; Two vector fields are used to describe this force. The first is the electric field, which describes the force acting on a stationary charge and gives the component of the force that is independent of motion. The magnetic field, on the other hand, describes the component of force that is proportional to both the velocity and the direction of the charged particles. The field is defined by Lorentz's law and is, at each instant, perpendicular to both the motion of the load as well as the force it experiences.

The name magnetic field or magnetic field intensity is applied to two magnitudes:

La magnetic excitation or field H is the first of them, from the historical point of view, and is represented with H.
La magnetic induction or field Bwhich is currently considered the real magnetic field, and is represented with B.

From a physical point of view, both are equivalent in the vacuum, except in a constant proportionality (permeability) that depends on the unit system: 1 in the Gauss system, $mu _{0}=4pi cdot 10^{{-7}}{{mbox{N}}}{{mbox{A}}^{{-2}}}$ in the SI. They only differ in material means with the phenomenon of magnetization.

Use

The H field has traditionally been considered the main field or magnetic field intensity, since it can be related to charges, masses or magnetic poles by means of a law similar to Coulomb's for electricity. Maxwell, for example, used this approach, while clarifying that these charges were fictitious. With this, not only is it based on similar laws in electric and magnetic fields (including the possibility of defining a magnetic scalar potential), but also in material media, with the mathematical equation of H with E, on the one hand, and from B to D, on the other, useful parallels can be drawn in boundary conditions and thermodynamic relations; the corresponding formulas in Gauss's electromagnetic system are:

${begin{array}{lll}{mathbf {B}}=mu {mathbf {H}}&qquad &{mathbf {H}}={mathbf {B}}-4pi {mathbf {M}}\{mathbf {D}}=epsilon {mathbf {E}}&&{mathbf {E}}={mathbf {D}}-4pi {mathbf {P}}end{array}}$

In electrical engineering it is not uncommon for this point of view to be maintained because it is practical.

With the advent of Lorentz and Poincaré's theories of the electron, and Einstein's relativity, it became clear that these parallels do not correspond to the physical reality of the phenomena, which is why it is common today, especially in physics, that the name magnetic field is applied to B (for example, in the texts by Alonso-Finn and Feynman). In the relativistic formulation of electromagnetism, E does not group with H for the intensity tensor, but with B.

In 1944, F. Rasetti prepared an experiment to determine which of the two fields was the fundamental one, that is, the one that acts on a moving charge, and the result was that the real magnetic field was B and not H.

In order to characterize H and B, several distinctions have been made. Thus, H describes how strong the magnetic field is in the region it affects, while B is the amount of magnetic flux per unit area that appears in that same region. Another distinction sometimes made is that H refers to the field in terms of its sources (electrical currents) and B to the field in terms of its effects (forces on the loads).

Relation between H and B

The formulas derived for the magnetic field above are correct when it comes to the full current. However, a magnetic material placed within a magnetic field generates its own magnetization, which can be challenging to calculate. (This bound current is due to the sum of atomic-sized current loops and the spin of the subatomic particles, such as electrons, that make up the material.) The $H$ field, as defined above, helps to factor this bound current; but to see how, it helps to first introduce the concept of magnetization.

International symbol of intense magnetic field warning (used whatever its origin).

Magnetization

Main article: Magnetization

The vector field of magnetization $M$ represents the force with which a region of material is magnetized. It is defined as the net magnetic dipole moment per unit volume of that region. The magnetization of a uniform magnet is therefore a material constant, equal to the magnetic moment $m$ of the magnet divided by its volume. Since the SI unit of magnetic moment is A⋅m², the SI unit of magnetization $M$ is the ampere per meter, identical to the $H$ field.

The magnetizing field $M$ of a region points in the direction of the mean magnetic dipole moment in that region. The magnetizing field lines therefore start near the south magnetic pole and end near the north magnetic pole. (Magnetization does not exist outside of the magnet.)

In the amp loop model, magnetization is due to the combination of many tiny amp loops to form a resultant current called ligated current. This bound current, then, is the source of the magnetic field $B$ due to the magnet. (See Magnetic dipoles below and Magnetic poles vs. atomic currents for more information.) Given the definition of a magnetic dipole, the magnetizing field follows a law similar to Ampere's law:

{displaystyle oint mathbf {M} cdot mathrm {d} {boldsymbol {ell }}=I_{mathrm {b} },}

where the integral is a line integral over any closed loop and $I b$ is the limit current enclosed by that closed loop.

In the magnetic poles model, magnetization begins and ends at the magnetic poles. Therefore, if a given region has a "magnetic pole force" net positive (corresponding to a north pole), then it has more magnetizing field lines entering it than leaving it. Mathematically this is equivalent to:

{displaystyle oint _{S}mu _{0}mathbf {M} cdot mathrm {d} mathbf {A} =-q_{mathrm {M} }}

where the integral is a closed surface integral over the closed surface $S$ and $q M$ is the "magnetic charge" (in units of magnetic flux) enclosed by $S$ . (A closed surface completely surrounds a region with no holes to let the field lines escape.) The negative sign occurs because the magnetizing field moves from south to north.

H field and magnetic materials

In SI units, the H field is related to the B field by

{displaystyle mathbf {H} equiv {frac {mathbf {B} }{mu _{0}}}-mathbf {M}.}

In terms of the H field, Ampere's law is

{displaystyle oint mathbf {H} cdot mathrm {d} {boldsymbol {ell }}=oint left({frac {mathbf {B} }{mu _{0}}}-mathbf {M} right)cdot mathrm {d} {boldsymbol {ell }}=I_{mathrm {tot} }-I_{mathrm {b} }=I_{mathrm {f} },}

where $I f$ represents the "free current" enclosed by the loop, so the line integral of $H'$ does not depend on the bound currents at all.

For the differential equivalent of this equation see Maxwell's Equations. Ampere's law leads to the boundary condition.

{displaystyle left(mathbf {H_{1}^{parallel }} -mathbf {H_{2}^{parallel }} right)=mathbf {K} _{mathrm {f} }times {hat {mathbf {n} }},}

where $K f$ is the surface free current density and the normal unit ${displaystyle {hat {mathbf {n} }}}$ points in the direction of middle 2 to mid 1.

Similarly, a surface integral of $H$ over any closed surface is independent of free currents and picks up the "charges magnetic" inside that closed surface:

{displaystyle oint _{S}mu _{0}mathbf {H} cdot mathrm {d} mathbf {A} =oint _{S}(mathbf {B} -mu _{0}mathbf {M})cdot mathrm {d} mathbf {A} =0-(-q_{mathrm {M} })=q_{mathrm {M} },}

which does not depend on free currents.

The $H$ field can therefore be separated into two independent parts:

{displaystyle mathbf {H} =mathbf {H} _{0}+mathbf {H} _{mathrm {d} },,}

where $H 0$ is the applied magnetic field due to free currents only and $H d$ is the demagnetizing field due to bound currents alone.

The magnetic field $H$ therefore refactors the bound current in terms of "magnetic charges". The $H$ field lines loop only around the "free current" and, unlike the $B$ magnetic field, it also begins and ends near the magnetic poles.

Magnetism

Main article: Magnetism

Most materials respond to an applied $B$ field by producing their own magnetization $M$ and thus its own $B$ fields. Normally the response is weak and only exists when the magnetic field is applied. The term magnetism describes how materials respond at the microscopic level to an applied magnetic field and is used to categorize the magnetic phase of a material. Materials are divided into groups based on their magnetic behavior:

Dismagnetic materials produce a magnetization that opposes the magnetic field.
Paramagnetic materials produce a magnetization in the same direction as the applied magnetic field.
Ferrromagnetic and closely related materials Pherremagnetic materials and antiferromagnetic materials may have an independent magnetization of a field B applied with a complex relationship between the two fields.
Superconductors (and superconductor ferrommetic)

They are materials that are characterized by perfect conductivity below a critical temperature and magnetic field. They are also highly magnetic and can be perfect diamonds below a lower critical magnetic field. Superconductors typically have a wide range of temperatures and magnetic fields (the so-called Mixed State) under which they exhibit a complex hysteretic dependence of $M$ on $B$ .

In the case of paramagnetism and diamagnetism, the magnetization $M$ is usually proportional to the applied magnetic field such that:

{displaystyle mathbf {B} =mu mathbf {H}}

where $μ$ is a material-dependent parameter called permeability. In some cases, permeability may be a second rank tensor, so $H$ may not point in the same direction as $B$ . These relationships between $B$ and $H$ are examples of a constitutive equation. However, superconductors and ferromagnets have a more complex relationship between $B$ and $H$ ; see magnetic hysteresis.

Sources of the magnetic field

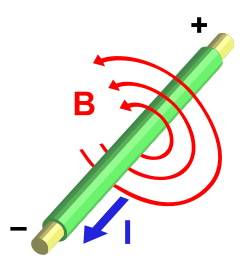
Iron stains showing the magnetic field of a rod magnet produced by a magnet under the paper.

A magnetic field has two sources that cause it. One of them is a conducting electric current, which gives rise to a static magnetic field, if it is constant. On the other hand, a displacement current originates a time-varying magnetic field, even though it is stationary.

The relationship between the magnetic field and an electric current is given by Ampère's law. The most general case, which includes displacement current, is given by the Ampère-Maxwell law.

Magnetic field produced by a point charge

The magnetic field generated by a single moving charge (not by an electric current) can be roughly calculated from the following expression derived from the Biot-Savart law:

${mathbf {B}}={frac {mu _{0}}{4pi }}{frac {(q{mathbf {v}})times {hat {{mathbf {u}}}}_{r}}{r^{2}}}$

Where $mu _{0}=4pi cdot 10^{{-7}}{frac {{mbox{N}}}{{mbox{A}}^{2}}}$ . This last expression defines a solenoidal vector field, for distributions of moving loads the expression is different, but it can be proved that the magnetic field remains a solenoidal field. It is an approximation because, starting from a continuous stream of loads and trying to transform the law for punctual charges, the interactions between the loads of the current are despised. This approach is useful for low speeds (spect to the speed of light).

Magnetic field produced by a distribution of charges

The absence of magnetic loads leads to the magnetic field being a solenoidal field, which leads to the locality being derived from a potential vector ${mathbf {A}}$ I mean,

${mathbf {B}}=nabla times {mathbf {A}}$

In turn, this potential vector can be related to the current density vector through the relationship:

$Delta {mathbf {A}}=mu _{0}{mathbf {j}}$

The previous equation $scriptstyle mathbb{R} ^{3}$ , with a distribution of loads contained in a compact set, the solution is expressed as integral. And the magnetic field of a load distribution is given by:

${mathbf {B}}({mathbf {r}})={frac {mu _{0}}{4pi }}int _{{V_{1}}}{frac {{mathbf {j}}_{1}times {mathbf {{hat {u}}}}_{r}}{|{mathbf {r}}-{mathbf {r}}_{1}|^{2}}} {mathrm {d}}V_{1}$

Inexistence of isolated magnetic charges

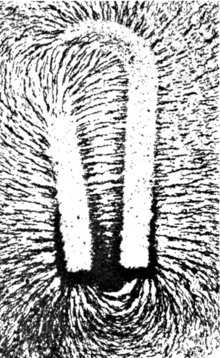
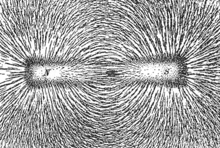
It should be noted that, unlike the electric field, in the magnetic field the existence of magnetic monopoles has not been proven, only magnetic dipoles, which means that the magnetic field lines are closed, that is, the net number of field lines entering a surface is equal to the number of field lines leaving the same surface. A clear example of this property is represented by the field lines of a magnet, where it can be seen that the same number of field lines that leave the north pole re-enter the south pole, from where they return inside the magnet. up north.

Illustration of a magnetic field around a wire through which electric current flows.

As can be seen in the drawing, regardless of whether the moving charge is positive or negative, at point A there is never a magnetic field; however, at points B and C the magnetic field reverses its direction depending on whether the charge is positive or negative. The direction of the magnetic field is given by the right-hand rule.

To determine the direction, a vector is taken ${displaystyle q{vec {v}}}$ , in the same direction of the trajectory of the load in motion. The direction of this vector depends on the sign of the load, that is, if the load is positive and moves to the right, the vector ${displaystyle +q{vec {v}}}$ It will be oriented to the right. However, if the load is negative and moves to the right, the vector ${displaystyle -q{vec {v}}}$ Go left. Then it runs pointing with the four fingers of the right hand, from the first vector ${displaystyle q{vec {v}}}$ until the second vector ${displaystyle U{vec {r}}}$ , on the shortest road or, what is the same, the path that forms the lower angle between the two vectors. The extended thumb will indicate at that point the direction of the magnetic field.

Energy stored in magnetic fields

Energy is needed to generate a magnetic field, to work against the electric field that a magnetic field creates, and to change the magnetization of any material within the magnetic field. For non-dispersive materials, this same energy is released both when the magnetic field is destroyed in order to model this energy, and when it is stored in the magnetic field.

For linear and non-dispersive materials (such as $scriptstyle B=mu H$ where μ is independent of frequency), energy density is:

${mathcal {E}}_{M}={frac {B^{2}}{2mu }}={frac {mu H^{2}}{2}}$

If there are no magnetic materials around, then μ can be substituted for μ₀. The above equation cannot be used for non-linear materials, a more general expression given below is used.

Generally the incremental amount of work per δW of unit volume needed to cause a small δB change of the magnetic field is: δW= H*δB

Once the relationship between H and B is obtained, this equation is used to determine the work needed to reach a given magnetic state. For materials like ferromagnetics and superconductors the work needed will also depend on how the magnetic field is created.

Determination of the magnetic induction field B

The figure shows the relationships between the vectors. It is observed that:
* (a) the magnetic force is canceled when

,!vto 0

,
* (b) the magnetic force is canceled if v is parallel or anti-parallel to the direction of B (in these cases

,!theta =0^{circ }

,!theta =180^{circ }

and

{vec v}times {vec B}=0

)
*(c) yes v is perpendicular to B (

,!theta =90^{circ }

) the deviant force has its maximum value, given by:

,!F_{perp }=q_{0}vB

The magnetic field for loads that move at small speeds compared to light speed can be represented by a vector field. Be a test electric charge $q_{0}$ in a point P of a region of space moving to a certain arbitrary speed v regarding a certain observer who does not detect electric field. If the observer detects a deflection of the trajectory of the particle then in that region there is a magnetic field. The value or intensity of the magnetic field can be measured by the so-called magnetic induction vector Bsometimes called simply "magnetic field", which will be related to force F and speed v by such observer at point P: If the direction of v by P, without changing its magnitude, it is generally found that the magnitude of F varies, although it is preserved perpendicular to v. From the observation of a small electric test load, the direction and module of the vector can be determined as follows:

The direction of the "magnetic field" is defined operationally as follows. For a certain address v, force F It's over. This direction is defined as that of B.
Once this address is found the magnetic field module can be easily found as it is possible to guide v in such a way that the test load is shifted perpendicularly to B. It finds, then, that the F is maximum and the magnitude of B determining the value of that maximum force:

$B={frac {F_{perp }}{q_{0}v}}$

Accordingly: If a positive test load $q_{0}$ shoots with a speed v by a point P and if you work a side force F on the load moving, there's a magnetic induction B in point P being B the vector that satisfies the relationship:

${mathbf {F}}=q_{0}{mathbf {v}}times {mathbf {B}}$

The magnitude of F, according to the cross product rules, is given by the expression:

${displaystyle ,!F=q_{0}vBsin(theta)}$

Expression in which $theta ;$ is the angle between v and B.

The fact that the magnetic force is always perpendicular to the direction of the movement implies that the work done by it on the load is zero. Indeed, for a length element $,!dl$ of the trajectory of the particle, the work $,!dW$ That's it. ${displaystyle ,!{vec {F}}_{B}cdot dl}$ That's worth zero. $,!F$ and $,!dl$ perpendicular. Thus, a static magnetic field cannot change the kinetic energy of a moving load.

If a charged particle moves through a region in which an electric field and a magnetic field coexist, the resultant force is given by:

$,!{vec F}=q_{0}{vec E}+q_{0}{vec v}times {vec B}$

This formula is known as the Lorentz ratio.

Magnetic field in relativity

Field measured by two observers

The theory of special relativity proved that in the same way that space and time are not absolute concepts, the electrical and magnetic part of an electromagnetic field depends on the observer. That means two observers. $scriptstyle {mathcal {O}}$ and $scriptstyle {bar {{mathcal {O}}}}$ in relative motion one with respect to another the magnetic and electric field measured by each of them will not be the same. In the context of special relativity if the two observers move one over another with uniform speed v directed according to the X axis, the components of the electric fields measured by one and another observer will be related by:

${bar {E}}_{x}=E_{x},quad {bar {E}}_{y}={frac {E_{y}-vB_{z}}{{sqrt {1-v^{2}/c^{2}}}}},quad {bar {E}}_{z}={frac {E_{z}+vB_{y}}{{sqrt {1-v^{2}/c^{2}}}}}$

And for the magnetic fields we will have:

${displaystyle {bar {B}}_{x}=B_{x},quad {bar {B}}_{y}={frac {B_{y}+vE_{z}/c^{2}}{sqrt {1-v^{2}/c^{2}}}},quad {bar {B}}_{z}={frac {B_{z}-vE_{y}/c^{2}}{sqrt {1-v^{2}/c^{2}}}}}$

Note that in particular an observer at rest relative to an electric charge will detect only an electric field, while observers moving relative to the charges will detect an electric and magnetic part.

Field created by a moving charge

The magnetic field created by a moving charge can be proved by the general relationship:

${mathbf {B}}={mathbf {v}}times {mathbf {E}}/c^{2}$

which is valid both in Newtonian mechanics and in relativistic mechanics. This leads to the fact that a point charge moving at speed v provides a magnetic field given by:

${displaystyle mathbf {B} ={frac {mu _{0}q}{4pi r^{2}}}{frac {1-v^{2}/c^{2}}{[1-(v^{2}/c^{2})sin ^{2}theta ]^{3/2}}}mathbf {v} times mathbf {u} _{r}}$

where the angle $theta$ is the angle formed by the vectors ${mathbf {v}}$ and ${mathbf {u}}_{r}$ . If the magnetic field is created by a charged particle that has acceleration the previous expression contains additional terms (see Liénard-Wiechert potentials).

Typical units and quantities

Main articles: Tesla (unit), Gauss (electromagnetic unit) and Oersted (unit).

The SI unit of B is the tesla, which is equivalent to wéber per square meter (Wb/m²) or volt-second per square meter (V s/m²); in base units it is kg s⁻² A⁻¹. Its unit in the Gaussian system is the gauss (G); In base units it is cm^−1/2 g^1/2 s⁻¹.

The SI unit of H is the ampere per meter, A/m (sometimes called amperevolt per meter, Av/m). Its unit in the Gauss system is the oersted (Oe), which is dimensionally equal to the Gauss.

The magnitude of the Earth's magnetic field at the Earth's surface is about 0.5G. Common iron permanent magnets generate fields of a few hundred Gauss, that is, at short range the influence on a compass is about a thousand times more intense than that of the terrestrial magnetic field; since the intensity is reduced with the cube of the distance, at relatively short distances the earth's field again dominates. The most powerful commercial magnets, based on combinations of transition metals and rare earths, generate fields up to ten times stronger, up to 3000-4000 G, that is, 0.3-0.4 T. The theoretical limit for permanent magnets is about ten times higher, about 3 Tesla. Specialized research centers routinely obtain fields up to ten times more intense, about 30T, using electromagnets; this limit can be doubled by pulsed fields, which allow the conductor to cool down between pulses. In extraordinary circumstances, it is possible to obtain fields even of 150 T or higher, by means of explosions that compress the field lines; naturally in these cases the field lasts only a few microseconds. On the other hand, the fields generated naturally on the surface of a pulsar are estimated to be in the order of hundreds of millions of Tesla.

Display

Main article: Field line

The direction of magnetic field lines represented by sprinkled iron clamps on a paper placed above a magnetic bar

The field can be visualized by a set of magnetic field lines, which follow the direction of the field at each point. The lines can be constructed by measuring the strength and direction of the magnetic field at a large number of points (or at every point in space). Each location is then marked with an arrow, called a vector, pointing in the direction of the local magnetic field with its magnitude proportional to the magnetic field strength. The connection of these arrows forms a set of magnetic field lines. The direction of the magnetic field at any point is parallel to the direction of the nearby field lines, and the local density of field lines can be made proportional to their strength. Magnetic field lines are like streamlines in fluid flow, in that they represent a continuous distribution, and a different resolution would show more or fewer lines.

The compass needles point in the direction of the local magnetic field, towards the south pole of a magnet and far from its north pole

One advantage of using magnetic field lines as a representation is that many laws of magnetism (and electromagnetism) can be stated completely and concisely using simple concepts such as "number" of field lines passing through a surface. These concepts can be "translated" quickly to its mathematical form. For example, the number of field lines through a given surface is the surface integral of the magnetic field.

Several phenomena "show" magnetic field lines as if field lines were physical phenomena. For example, iron filings placed in a magnetic field form lines that correspond to "field lines". The "lines" The magnetic field also shows up visually in the aurora borealis, in which dipole interactions of plasma particles create visible streaks of light that align with the local direction of Earth's magnetic field.

Field lines can be used as a qualitative tool to visualize magnetic forces. In ferromagnetic substances such as iron and in plasmas, magnetic forces can be understood by imagining that the field lines exert a tension, (like a rubber band) along their length, and a pressure perpendicular to their length on the lines. neighboring fields. The "different" Magnets attract each other because they are linked by many field lines; the "similar" they repel each other because their field lines do not meet, but instead run parallel, pushing each other. The rigorous form of this concept is the electromagnetic impulse-energy tensor. In the microscopic world, taking into account the values of the dipole moment of typical magnetic ions and the equation that governs the propagation of the field generated by a magnetic dipole, it is verified that at a distance of one nanometer, the magnetic field generated by an isolated electron is of order of 3 G, that of a typical magnet molecule, of the order of 30 G, and that of a typical magnetic ion can have an intermediate value, from 5 to 15 G. To an angstrom, which is a common value for an atomic radius and therefore the minimum value for which it can make sense to refer to the magnetic moment of an ion, the values are a thousand times higher, that is, of the order of magnitude of the Tesla.

Contenido relacionado

Más resultados...