Magic square
A magic square is a table of primary degree where a series of integers are arranged in a square or matrix in such a way that the sum of the numbers by columns, rows, and main diagonals is the same. Usually the numbers used to fill in the boxes are consecutive, from 1 to n², where n is the number of columns and rows of the magic square.
Magic squares currently have no known technical application that benefits from these features, so they remain confined to amusement, curiosity, and mathematical thinking. Apart from this, in the occult sciences and more specifically in magic they have a prominent place. In some types of oriental techniques, as in the case of Ba Gua and Feng Shui, magic squares are very important, both for philosophical and numerological reasons as well as for practical ones, for example, when determining orientations and specific spaces.
Introduction
Let's consider the mathematical sequence 1, 2, 3, 4... 36 (square of order 6), and let's arrange the numbers in two zig-zag arranged series:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 36 | 35 | 34 | 33 | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 |
It is evident that any pair of numbers aligned vertically adds the same, since as we move through the columns, the top row adds one unit, while the bottom row subtracts one. The sum is in all cases that of the extreme numbers:
- n2+1=36+1=37{displaystyle n^{2}+1=36+1=37}
| 1 | 2 | 3 | 4 | 5 | 6 |
| 12 | 11 | 10 | 9 | 8 | 7 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 24 | 23 | 22 | 21 | 20 | 19 |
| 25 | 26 | 27 | 28 | 29 | 30 |
| 36 | 35 | 34 | 33 | 32 | 31 |
If we arrange the set of numbers in six rows (see table on the right), it can easily be seen that the sums in the different columns must necessarily be equal, since the numbers are grouped in pairs as they were in the first case (compare the 1st-6th, 2nd-5th and 3rd-4th row pairs with the original arrangement). Now, however, since there are three pairs of rows (n/2), the sum will be:
- M2(n)=n(n2+1)2{displaystyle M_{2}(n)={frac {n(n^{2}+1)}{2}}}}{2}}}
quantity called the magic constant, which in our case is n×(n² + 1)/2 = 6× (36 + 1)/2 = 111.
| Order n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| M2 (n) | 15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |
It is obvious that the previous table is not a magic square, since when the numbers are arranged consecutively, the sums of the figures in each row are greater each time. However, we have found six series of numbers between 1 and 36, in such a way that, without repeating any, the sums of the series are the magic constant. If instead of the previous arrangement we place the numbers consecutively, we obtain an arrangement in which the numbers on the main diagonal can be written in the form (a-1)×n + a.
Calculating the sum, knowing that rows a go from 1 to n:
␡ ␡ a=1n(a− − 1)n+a=(n+1)␡ ␡ a=1na− − ␡ ␡ a=1nn=(n+1)n(1+n)2− − n2=n3+2n2+n− − 2n22=n(n2+1)2{displaystyle sum _{a=1}{n}(a-1){n} +a=(n+1)sum _{a=1}{n}{a-sum _{a=1}{n}{n}{n=(n+1){n(1+n)}{2}{2}{2⁄2}{frac}{n}{2⁄2⁄2⁄2⁄2⁄2⁄2⁄2}}}}}{n}{2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2}}}}}}{1⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2⁄2}}}}}}
The magic constant again. Furthermore, any series of six values where no two are in the same row or column will add up to the magic constant. Writing the term i, j of the array as (i-1)×n + j , and taking any 6 terms with the condition that neither i, nor j are repeated and vary from 1 to n, the resulting equation will be exactly the same as in the previous case and the sum, therefore, the magic constant.
As can be shown, the number of possible series of n numbers satisfying the above condition is n!, 720 in squares of order 6, and they are not even all the possible ones, since before we had obtained six that are not included among them.
There is a single magic square of order 3 (the different variations can be obtained by rotation or reflection), in 1693 Bernard Frenicle de Bessy established that there are 880 classes of magic squares of order 4. It has subsequently been found that there are 275,305,224 magic squares of order 5; the number of squares of higher order is still unknown, but according to estimates by Klaus Pinn and C. Wieczerkowski carried out in 1998 using the Monte Carlo and statistical mechanics methods, there are (1.7745 ± 0.0016) × 1019 squares of order 6 and (3.7982 ± 0.0004) × 1034 squares of order 7.
As far as lower orders are concerned, it is clear that of order one there is a single magic square, 1 , while of order 2 there is none, which can be proved by considering the magic square a, b, c, d of the figure; For such an arrangement to be a magic square, the following equations should hold (where M is the magic constant or any quantity, if desired):
|
|
writing the system of equations in matrix form and looking for the order of the matrix of coefficients, it is obtained that it is three, while the number of unknowns is four, so that the system only has the trivial solution a = b = c = d = M/2 being impossible to construct a magic square on the that the four figures are different.
Summarizing: the number of different n×n magic squares for n between 1 and 5, not counting rotations and reflections , they are:
- 1, 0, 1, 880, 275305224 (A006052 succession in OEIS).
For s = 6 it has been estimated that there are approximately 1.7745×1019.

The Astronomical Phenomena (Tien Yuan Fa Wei).
Compiled by Bao Yunlong in the 13th century,
Ming Dynasty, 1457-1463.
History
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Many of the historical aspects of magic squares are not preserved. And being verifiable, these aspects are unnecessary. The painting Melancholy I 1514 by Albrecht Dürer still exists, as does the Sagrada Família building.
In ancient China, magic squares were already known since the 3rd millennium BC. C., as the Lo Shu says. According to legend, a certain day a river overflowed; The people, fearful, tried to make an offering to the god of the river Lo (one of those that overflowed) to calm his anger. However, each time they did so, a turtle would appear, hovering around the offering without accepting it, until a boy noticed the peculiar marks on the turtle's shell, thus they were able to include the requested amount in their offering (15)., leaving the god satisfied and returning the waters to their course.
Indians, Egyptians, Arabs and Greeks also knew combinations of this class. Different cultures have attributed marvelous astrological and divinatory properties to such squares, often being engraved on talismans. Thus, as stated by Cornelius Agrippa in De occulta philosophia libri tres (1533), the square of order 3 (15) was dedicated to Saturn, that of 4 (34) to Jupiter, that of 5 (65) to Mars, the one from 6 (111) to the Sun, the one from 7 (175) to Venus, the one from 8 (260) to Mercury and the one from 9 (369) to the Moon; The same attribution can be found in Hindu astrology.
The introduction of magic squares in the West is attributed to Manuel Moscópulo around the 14th century, author of a manuscript in which for the first time some methods for constructing them are explained. Subsequently, the study of its properties, already of a scientific nature, attracted the attention of great mathematicians who dedicated various works to the subject despite the manifest practical uselessness of magic squares. Among them it is worth mentioning Stifel, Fermat, Pascal, Leibnitz, Frénicle, Bachet, La Hire, Saurin, Euler,... it would seem that no illustrious mathematician has been able to escape his spell.
Dürer's Magic Square
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
- The magical square of Alberto Durero, carved in his work Melancholy I is considered the first of the European arts. In the square of order four you get the magic constant (34) in rows, columns, main diagonals, and in the four submatrics of order 2 in which the square can be divided, adding the numbers of the corners, the four central numbers, the two central numbers of the rows (or columns) first and last, etc. and being the two central figures of the last row 1514 the year of execution of the work.
Some particular arrangements in Dürer's magic square that add up to the magic constant.
|
|
|
|
|
The magic square of the Sagrada Familia
The Passion Facade of the Expiatory Temple of the Sagrada Familia in Barcelona, designed by the sculptor Josep María Subirachs, shows a magic square of order 4.
The magic constant of the square is 33, the age of Jesus Christ at the Passion. The choice of this number has also been attributed as a veiled allusion to the supposed Masonic affiliation, which has never been proven, of Antonio Gaudí, since 33 are the traditional degrees of Freemasonry. Structurally, it is very similar to the magic square in Melancholy, but two of the numbers in the square (12 and 16) are decreased by two units (10 and 14), so repetitions appear. This allows the magic constant to be lowered by 1.
Magic Square "Virgin of Calvary" by Zurgena
All of us who, more or less frequently, visit where the Virgin of Calvary is venerated, familiarly known as “Virgencica” of Calvary You have been able to observe the various works that have been carried out since 1992 for its conservation and adaptation, especially the arrangement of the roofs as the only possible alternative to avoid their collapse.
Both in the first conservation works and those that we are currently carrying out to expand, an important part of the necessary funds have been obtained mainly from the sale of NUMBER 54.713 of the Christmas Lottery and the existing LOTERÍA PRIMITIVA.
As a tribute to all those who collaborate with their economic contribution by participating in one of these games and so that the memory lasts over time, on one of the sides of the expansion works (detailed photos are attached location), there are two plaques with the numbers that make up each of the aforementioned games -Lottery and Primitiva-, which they are distributed in a somewhat special way and linking them together with a series of characteristics and peculiarities, as indicated below for knowledge in general and for collaborators in particular.
- Them magical squares, are a set of different integers placed in the boxes of a square and that are characterized because the sums of its main rows, columns and diagonals is always the same, the value of the sum is called Magic Constant of the Square. Numbers used to fill the boxes are consecutive, of n2, being n the number of columns and rows of the magic square.
- There are many variants of simple magic squares, as well as alternative methods of building them. Here we are limited to making a brief description of some of the existing variants.
- There are, magical squares that continue to be magical when they are removed from an outer band; even there are those that remain magical if they are removed from a band and then a second band. These features bring them together “our magical square.”
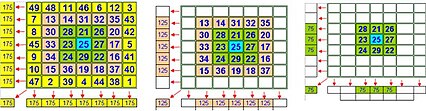
- The magical square of “Virgen del Calvario” is of order 7, it has by magic constant 175 (the forty-nine numbers of the game); the inner square is of order 5 that includes the central numbers of the previous series (37), it is also magical and has by magic constant 125, like the square of order three central (numbers 22) that has a magical constant 75.
- The amount in the form of a cross of the numbers is:100
- The amount of the tips of the numbers of the boxes is:100
- The amount of the square of the numbers that form the number of NAVITY is: 100
- By joining all the boxes in a correlative way with a line from number 1 to number 49, we can see that a “Eastern Star” in whose center the box is found with the number 25 and on this day of the month of December, Christians celebrate the birth of Jesus and this month also plays Christmas.
Magic Square of Foz
This magic square on the façade of a house in Foz (Lugo) has the numbers on tiles of four different non-repeating colors (red, yellow, blue and green) in none of the 20 groups of four numbers that have the magic constant of 34
4 vertical lines, 4 horizontal lines, 2 diagonal lines, the 4 corners of the square and the 4 corners of the 4 3x3 squares, 5 2x2 squares (the center of the square and those that make up the fourth part of the square)
Arithmetic Magic Square
Odd Order Magic Squares (I)
These squares can be generated according to the method published in 1691 by Simon de la Loubere, sometimes called the Siamese method, a country in which he served as ambassador of Louis XIV, method already known by Eastern astrologers. Beginning in the central square of the first row with the first number, the broken diagonal is filled with the following ones in the NW (or NE) direction. Once the first diagonal is completed, one position is lowered and the second is filled in in the same direction as the previous one, repeating the previous step with the rest of the diagonals until the square is completed. Pythagorean Triples and Magic Squares are ordered precisely in Odd Order Magic Squares

Obviously, it could have started in any of the central squares of the perimeter rows or columns, being in each case the direction of the diagonals towards the outside of the square and the direction of displacement once each diagonal is finished that given by the position relative of the center of the square with respect to the initial square.
It is evident that starting from any other box, the sums of the rows and columns will be the magic constant, since the relative position of the figures will be the same as in the previous case; however, in the diagonal parallel to the filling direction this condition will not be met (it will be in the other). In fact, the particular choice of the initial box responds to the need for the five central numbers of the series to be placed consecutively on the diagonal parallel to the filling direction, since any other five consecutive numbers will not add up to the magic constant.
Odd Order Magic Squares (II)
Step 1: Write the numbers from 1 to n². The 1 is written in the upper box of the rhombus and it will be followed obliquely as seen in this example. The magic square will be a square inscribed in the rhombus that we have formed.
| 1 | ||||||||
| 6 | 2 | |||||||
| 11 | 7 | 3 | ||||||
| 16 | 12 | 8 | 4 | |||||
| 21 | 17 | 13 | 9 | 5 | ||||
| 22 | 18 | 14 | 10 | |||||
| 23 | 19 | 15 | ||||||
| 24 | 20 | |||||||
| 25 |
Step 2: We move the numbers from the corners of the rhombus to the empty squares on the opposite side of the square.
| 1 | ||||||||
| 6 | 2 | |||||||
| 11 | 24 | 7 | 20 | 3 | ||||
| 16 | 4 | 12 | 25 | 8 | 16 | 4 | ||
| 21 | 17 | 5 | 13 | 21 | 9 | 5 | ||
| 22 | 10 | 18 | 1 | 14 | 22 | 10 | ||
| 23 | 6 | 19 | 2 | 15 | ||||
| 24 | 20 | |||||||
| 25 |
Step 3: We remove the corners of the rhombus: we already have a magic square of odd order.
| 11 | 24 | 7 | 20 | 3 |
| 4 | 12 | 25 | 8 | 16 |
| 17 | 5 | 13 | 21 | 9 |
| 10 | 18 | 1 | 14 | 22 |
| 23 | 6 | 19 | 2 | 15 |
Magic squares of multiples of 4
A square is constructed with the numbers arranged consecutively (see the second square of order six in the introduction), an arrangement in which, as we know, the sums of the diagonals are the magic constant. Once this is done, and keeping the central submatrix of order n/2 and the four corner submatrixes of order n/4, the remaining numbers are rotated 180º with respect to the center of the square, or if you prefer, they are repositioned in decreasing order (in both cases the result is the same).
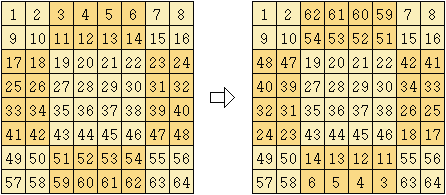
Starting from the same arrangement and choosing similar symmetrical patterns of the figures to be conserved, magic squares different from the one obtained before can be constructed, such as the following:
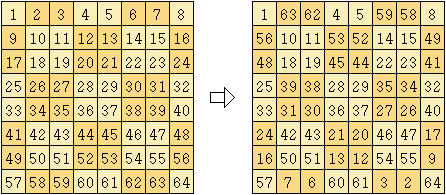
Magic squares of multiples of 4 plus 2
To build this kind of squares you can use the LUX method. It is based in part on the Loubere's method, which is used in the construction of odd-order magic squares (see above).
As an example, let's build a magic square with side 10.
1st step:
We are going to group the cells in 2x2 sub-squares, and we will label each of them as follows:
- The squares of the first k+1 rows, where k is the integer division of the size of the square by four, are labeled with the letter L (3 rows in this case).
- The squares in the next row are labeled with the letter U.
- The squares of the remaining rows are labeled with the letter X.
These letters will later tell us how to fill in each 2x2 subsquare.
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| U | U | U | U | U | |||||
| X | X | X | X | X |
2nd step:
Swap the central square U with the square L immediately above it.
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| L | L | U | L | L | |||||
| U | U | L | U | U | |||||
| X | X | X | X | X |
3rd step:
We will label each 2x2 subsquare with a number following the Loubere method. In this way we will indicate the order in which each sub-square is to be filled.
| 17 | 24 | 1 | 8 | 15 | |||||
| L | L | L | L | L | |||||
| 23 | 5 | 7 | 14 | 16 | |||||
| L | L | L | L | L | |||||
| 4 | 6 | 13 | 20 | 22 | |||||
| L | L | U | L | L | |||||
| 10 | 12 | 19 | 21 | 3 | |||||
| U | U | L | U | U | |||||
| 11 | 18 | 25 | 2 | 9 | |||||
| X | X | X | X | X |
4th step:
Now, the ith subsquare corresponds to the numbers 4i - 3, 4i - 2, 4i - 1 and 4i. For example, the subsquare 10 corresponds to the numbers 37, 38, 39, and 40.
We just need to know how the four numbers are placed inside their corresponding sub-square, and that's where LUX labeling comes into play.
| 4th Number | 1st Number |
| 2nd Number | 3rd Number |
| 1st Number | 4th Number |
| 2nd Number | 3rd Number |
| 1st Number | 4th Number |
| 3rd Number | 2nd Number |
As you can see, the letters are reminiscent of the shape numbers make when placed in each square.
With all these elements the square can be built:
| 68 | 65 | 96 | 93 | 4 | 1 | 32 | 29 | 60 | 57 |
| 66 | 67 | 94 | 95 | 2 | 3 | 30 | 31 | 58 | 59 |
| 92 | 89 | 20 | 17 | 28 | 25 | 56 | 53 | 64 | 61 |
| 90 | 91 | 18 | 19 | 26 | 27 | 54 | 55 | 62 | 63 |
| 16 | 13 | 24 | 21 | 49 | 52 | 80 | 77 | 88 | 85 |
| 14 | 15 | 22 | 23 | 50 | 51 | 78 | 79 | 86 | 87 |
| 37 | 40 | 45 | 48 | 76 | 73 | 81 | 84 | 9 | 12 |
| 38 | 39 | 46 | 47 | 74 | 75 | 82 | 83 | 10 | 11 |
| 41 | 44 | 69 | 72 | 97 | 100 | 5 | 8 | 33 | 36 |
| 43 | 42 | 71 | 70 | 99 | 98 | 7 | 6 | 35 | 34 |
Variants
There are many variants of the simple magic squares that we have just described, as well as alternative construction methods that can be found on the pages indicated below, so here we will limit ourselves to a brief description of some of them. existing variants.
| 49 | 48 | 11 | 46 | 6 | 12 | 3 |
| 7 | 13 | 14 | 31 | 32 | 35 | 43 |
| 8 | 30 | 28 | 21 | 26 | 20 | 42 |
| 45 | 33 | 23 | 25 | 27 | 17 | 5 |
| 9 | 34 | 24 | 29 | 22 | 16 | 41 |
| 10 | 15 | 36 | 19 | 18 | 37 | 40 |
| 47 | 2 | 39 | 4 | 44 | 38 | 1 |
There are, for example, magic squares that continue to be magic when an outer band is removed; there are even those that continue to be magical if one band is removed and then a second band is removed.
The complete square of the figure, of order 7, has the magic constant 175 (the first forty-nine numbers); the inner square of order 5, which includes the central numbers of the previous series (13 to 37), is also magical and has 125 as a magic constant, as is the central square of order three (numbers 21 to 29), which has a constant magic of 75.
| 7 | 2 | 11 | 14 |
| 9 | 16 | 5 | 4 |
| 6 | 3 | 10 | 15 |
| 12 | 13 | 8 | 1 |
Some squares preserve magic addition along all broken diagonals, as well as rows, columns, and main diagonals, like the one on the right. These arrangements are often called diabolical squares, although Dürer's square that does not meet this condition is also sometimes called that. The latter has also sometimes been called the satanic square because there are many combinations, certainly peculiar, of numbers symmetrically distributed throughout the matrix with which the magic sum is achieved, as we have already shown when we talk about him. In this regard, it should be remembered that the number of combinations of n digits, taken from the arithmetic series 1 to n×n, is even greater than that of squares that can be built with these figures, so finding apparently peculiar arrangements such that the magic sum is obtained is more common than it is believed. If we look, for example, at the diabolic square in the figure, we will see that such arrangements also add up to 34 (the four corners and the four central ones, the four submatrixes of order four, etc., and, in addition, the broken diagonals. Although in it the creation date of Melancholy I does not appear as it did in Dürer's magic square, in which there are more than 34 combinations).
If we understand magic squares as matrices, with their usual thumbnail and product operations, the magic square of order 3 has the interesting property that its inverse matrix again becomes a magic square having positive and negative fractional values and whose magic constant is 1/15.
This is the usual magic square of order 3...
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
...and this is your inverse magic square.
| 23/360 | -52/360 | 53/360 |
| 38/360 | 8/360 | -22/360 |
| -37/360 | 68/360 | -7/360 |
The p-magic squares are those such that raise all the digits of the square to the k power, where 1≤k≤p, they are still magical:
- The lesser known bi-magic square is that of order 8 shown later and has by magic constants 260 (k=1) and 11180 (k=2). It is conjecture that there are no bi-magic squares of lower order, although there is no conclusive proof of this. In 1998, J. R. Hendricks demonstrated that it is impossible to build bi-magic squares of order 3, except that which contains 9 equal figures, which of magic has rather little.
- Tri-magic squares of orders have been built 12, 32, 64, 81 and 128; the only order 12 was built by the German mathematician Walter Trump in June 2002.
- The first square tetra-magia, of order 64, got it Andrés González, in June 1998, using numbers from 1 to 4096 without repeating any of them. It can be segregated on 64 chess boards and would always add the same, indistinct position in which the north, south, east and west rows result. According to Gonzalez, no computer was used to block it. The picture is recorded in the Central International Archive for Art Objects. [2] (breakable link available on the Internet Archive; see history, first version and last).
- The first tetra-magic square, of order 512, was obtained by André Viricel and Christian Boyer in May 2001; in June of the same year they presented the first penta-magic square, of order 1024. Already in 2003, they presented a tetra-magic square of order 256 and the Chinese mathematician Li Wen one penta-magic of order 729.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bi-magic Square of Order 8 (magic 260 and 11.180) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tri-magic Square of Order 12 (magic 870, 83.810 and 9 082,800) |
Magic squares can be built with numbers extracted from any arithmetic sequence regardless of the initial number and the ratio of the series. Being a0 the first term and r the ratio, it is easily shown that the magic constant will be in this case:
- M2(n)=n[chuckles]2a0+(n2− − 1)r]2{displaystyle M_{2}(n)={frac {n[2a_{0}+(n^{2}-1)r]}{2}}}}}}
Similarly, magic squares can be constructed from geometric sequences, in which case it will be the products that result in the magic constant. These can be built with the rules given for arithmetic squares, simply by substituting the term of the geometric series in the position indicated by the corresponding term of the arithmetic series:
| Succession arithmetic
| ||||||||||||||||||||||||||||||
Correspondence
| Succession geometric
|
The magic constant is in the general case
- M2↓ ↓ (n)=(a02r(n2− − 1))n2{displaystyle {M_{2}}{*}{*}(n)=({a_{0}{2}{r^{(n^{2}-1}}}}}}}{frac {n}{2}}}}}}}
whose similarity with that already obtained for the arithmetic series is palpable.
Magic squares have also been built with series of consecutive prime numbers, or with the decimal figures of the reciprocals of the arithmetic series of natural numbers.
Lastly we will point out the existence of n-dimensional magical dispositions; thus, with series 1 - n³ you can build magic cubes, and in general, with series 1 - nr r-dimensional magic squares of order n, with their respective multi-magic variants and whose visualization is not immediate, although they can be handled comfortably using computers.
Esoteric Magic Squares
To the magician, a magic square is much more than to a mathematician the table of logarithms.
The use and importance in magic
Magic squares have been known since ancient times and have always been used in magic rituals. For the magician, the magic squares express in different planes, manifestations of the spiritual reality, a knowledge directly applicable in diverse forms. The most frequent are:
- Numerical values obtained by various formulas, which can be used to know exact quantities and proportions for certain operations (usually must meet certain standards).
- Signs that result from joining with specific lines numbers of a specific magical square. Such signs are known as signatures and refer to attributes (qualities) of the power to invoke. Such signs must be revealed by the entity to which the square is intended. To use them then, just draw them with a special ink on almost any surface and perform a simple ritual to request their attributes.
- The same esoteric magic square, engraved or made with precise materials and formulas and then consecrated in a ritual (which consists basically of prayers), can then be carried with it as talisman.
On the one hand, it is considered that each angel and demon (generally called intelligences, without entering hierarchies) is in tune (influence) with a certain square, something like what we understand today as resonance. On the other hand, the line drawing that results from traversing the values in the correct order, as well as other more complex orders, describe symbols (signatures) associated with spiritual entities, where in the correct ritual, drawing the sign with ink made expressly precisely, it is equivalent to invoking the spirit to which reference is made (calling it by its name), and where the evoked spirit is obliged to appear and/or to fulfill the virtues associated with the traced sign.
Summon entities with the help of magic square signs
In magic, summoning an entity by name is only possible if its name is previously known and pronounced correctly, which somehow carries certain risks. With the multiplicity of languages, this problem arises and therefore the correct pronunciation would render all previous knowledge useless, if the correct pronunciation of the names has not been transmitted with it.
Therefore, the advantage of the procedure of the lines of the magic square makes it universal. Even if you do not know the name of a spirit, correctly using the stroke model the invocation of the spirits is carried out. The magic squares are used to establish a correct appeal to a spiritual entity, marking the lines that said entity has established for itself. Once the entity appears, it can be demanded to express its name and even to teach it other attributes that the magician does not know about said entity.
There are two actions that are clearly distinguished in magic although colloquially they are often used interchangeably, it is necessary to differentiate them:
- Evoke: It is to request the presence of an entity, to appear before the magician. Where the magician is an entity manifests its presence through sounds, lights and shadows or more or less corporeal forms as well as smells and sounds quite indescribable some.
- Invoking: It is to request that a request be made. The entity does not act to appear, although the magician can receive internal impressions of his manifestation. Such manifestations, however, do not have to be received by other attendees if they have.
They are also used without requiring the presence of the referenced entities, through written requests, if the effect of the signs is already known, in which case, it is enough to trace the sign and make use of the pertinent sentences. Also, when you do not want to use signs or they are not known in a more general way, you can completely draw the square that corresponds to the entity that you want to invoke, together with one of its names, this is the case of the so-called amulets and talismans.
When an entity is evoked or invoked, use can be made of the properties (or powers) that the spiritual entity has been assigned. Starting from the magic square with which it is associated, there are different strokes that invoke each of its powers (attributes), and that are more reminiscent of any prayer formula typical of other traditions or religions.
It is common for an entity to have more than 1 name, since each name usually refers to one of its attributes.
In high magic, the first operation when an entity attends the call is to ask the magician to discover the different strokes that are his own, so that he can later invoke his powers. Once these are known, the magician has the obligation to jealously guard them, taking care that they do not fall into disgraceful hands and often the magician himself takes care to alter them at will (we would say encrypt them today) so that in such circumstances they cannot be used without a in-depth knowledge of both the stroke and what such powers imply.
The rituals to invoke the execution of the powers are relatively easy once the traces (attributes of the entity) are known, they are all a derivation of the main evocation ritual, where the requirement to appear is replaced by the request for what that is desired in the form of a prayer, both in one and in the other the virtues of the entity are praised and the blind confidence that it will fulfill what is requested, agreed or promised. The ritual always entails protection measures against intelligences hostile to the human race.
The magicians have always insisted on the aspirants in the importance of not trying to make use of them, without a deep theoretical knowledge before passing to the practical one, under the penalty of suffering indescribable torments in their own flesh.
Duration of effects
The magic square, the derived signs, etc... are useless if the magician does not make it following certain rules about materials to use, zodiacal aspects related to starting its elaboration, etc... as well as without the rituals end of consecration and use.
When a magic square is carried as a talisman, the consecration ritual is enough, the signs, on the other hand, require a ritual of use, since they only serve for the use for which they have been declared and only for that one time. The time that its effect should last depends on the use to which it is intended, for example if the appearance of a spirit is requested, its duration is ephemeral, therefore it lasts until the entity is fired, on the other hand if it is used, for example, to make grow a plant, its effect lasts a few months in time.
In general, for long-lasting effects, the entire magic square is used as a talisman. And for immediate effects, the signs that are drawn on the magic square are often used. Evocation is more powerful than summoning but also carries high risks for the magician, especially the aspiring magician who can easily be impressed and succumb to the entity's demands, especially if the entity appearing is hostile to the human race or one entity masquerades as another and the magician or would-be magician fails to take the necessary action.
Description of properties of esoteric magic squares
Note: to appreciate the comparisons, for the esoteric magic squares, other colors have been taken, different from those used up to here.
An esoteric magic square, uses more restrictive criteria in terms of conditions to be considered a magic square, so much so that there is only one for every n. In order to recognize which are esoteric and which are not (or being equivalent to reduce them to their correct expression) it is important to know the properties that relate and identify them.
- The equivalence property states that 2 or more squares are similar if all their boxes vary in the same proportion, the esoteric, cannot be any, but only 1, as expressed in its section, but that can be reduced to the equivalent esoteric magic square.
- The property of the corners proposes a quick method of discarding magical squares if they do not comply with such property, those who pass the broom cannot yet be admitted.
- The properties of the center, positional and diagonal aims to learn to recognize magical esoteric squares as well as to manufacture them.
Equivalence property
| 28 | 21 | 26 |
| 23 | 25 | 27 |
| 24 | 29 | 22 |
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
In an esoteric sense, only those that have the same digits as the number of squares (which follow the series of natural numbers from 1 to n²) are considered magic squares. The square in the figure (orange color, on the left) is not an esoteric magic square. In this case, it is the result of a magic square of n=3 whose figures have been added 20, compare with the original (orange color on the right) of n=3, looking at the location of the figures and their concordance.
Corner Property
- In a esoteric sense, a magical square, must bring together some sum conditions of its corners (which we call the Magic Figure-2, or second order). Explanation as found:
- If we call Composition to the summation of the numbers that make up the magic square: C= sub (1+2+3....)or also C= ((n2+1)×(n2/2)...
- ...and if we call Base Number (Nb) to Composition divided between the number of boxes that make up the square, we will have to Nb= C / (n2). The base number can also be calculated as follows: Nb= (n2+1)/2 (Refer to the attached table below the ratio of its figures between the two columns where Nb It's almost half of it. n2). The base number in an esoteric magical square of n= impar always appears in the central square, which in some way helps to recognize and reject from a simple glance those who do not comply with that condition. (See section positional properties below for more details).
- We also get the Magic Figure by multiplying the base number by n Cm=Nb×n (or inversely, we get Nb, by dividing the Magic Figure between n Nb= Cm/n).
| r | _ | _ | s |
| _ | _ | _ | _ |
| _ | _ | _ | _ |
| t | _ | _ | u |
| r | _ | s |
| _ | _ | _ |
| t | _ | u |
- And being Magic Figure-2 the sum of the corners then: Cm2= r+s+t+u
- Then Cm2, the sum of the corners Cm2= Cm - (Nb(n-4))
- Or also (parting from that Cm=Nb×n(c): Cm2= Nb×n - (Nb(n-4)).
- Or reducing: Cm2= 4Cm / n.
- In the drawings the corner boxes, for squares of n=4 and n=3
- It follows that if the square has less corners of 4, then that figure is added, that if it is greater than 4 corners, the figure is subtracted. For the case of 4 exact corners, neither is it added nor subtracted, or is added and subtracted (as you prefer to be considered).
- We can check that in the magic square of 4 the sum of the 4 corners Cm2 =Cm (Magic Figure2= Magical Figure).
Also the sum of the figures of the 4 boxes that form a cross (those that are in the middle between two adjacent corners), add up to Cm2. The particularity of n=even_odd produces two cases.
| _ | C | _ |
| R | _ | U |
| _ | Z | _ |
| _ | _ | C1 | C2 | _ | _ |
| _ | _ | _ | _ | _ | _ |
| R1 | _ | _ | _ | _ | U1 |
| R2 | _ | _ | _ | _ | U2 |
| _ | _ | _ | _ | _ | _ |
| _ | _ | Z1 | Z2 | _ | _ |
- For the case of n=impar: Cm2= C +R +U +Z (left drawing).
- And for the case of n=par the two adjacent boxes that form the cross in the same conditions, only in this case being two groups of 4 boxes, is twice CM; =2 Cm2): Cm2=(C1 +C2 +R1 +R2 + U1 +U2 +Z1 +Z2)/2 (drawing from the right).
A square of n=3 is shown for an example of an odd case, and one of n=6 for an example of an even case. Observe that in the even case, the two central squares of CROSS are taken, which is why we must then divide by two.
- The example shown above the magic square with the case of n= 7 has been framed in the table: when applying C=1225; Nb=25; Cm= 25×7=175; Cm2= 175- (25(7-4)=100
- You can check Cm2=R+S+T+U, (the corners, in yellow 22 + 4 + 46 + 28) = 100
- You can also check Cm2=C+R+U+Z,(the centers on the cross, in dark 41 + 13 + 9 + 37) = 100
- I mean C+R+U+Z=R+S+T+U
| side n of the square | Casillas ## | Summary (n2+1)×(n2/2) | Magical Figure C/n | Base number Cm/n | Magical Figure-2 Cm2= 4Cm / n |
| n | n2 | C | Cm | Nb | Cm2 |
| 1 | 1 | 1 | 1 | 1 | 4 No mag. |
| 2 | 4 | 10 | 5 | 2.5 | 10 No mag. |
| 3 | 9 | 45 | 15 | 5 | 20 |
| 4 | 16 | 136 | 34 | 8.5 | 34 |
| 5 | 25 | 325 | 65 | 13 | 52 |
| 6 | 36 | 666 | 111 | 18.5 | 74 |
| 7 | 49 | 1225 | 175 | 25 | 100 |
| 8 | 64 | 2080 | 260 | 32.5 | 130 |
| 9 | 81 | 3321 | 369 | 41 | 164 |
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
.
- It can be understood that the square of 1, does not have 4 corners, and yet its magic figure-2, is 4, as it cannot add more than 1, it remains out of being an esoteric magical square.
- The square of two, if it has 4 corners, but its magic figure-2 throws a result of 10, which is impossible. It is explained above in this article, why a magical square of n=2, is not (Cm does not work), and here also why it is not esoteric.
School properties
In an esoteric magic square the following condition is also met (in addition to everything previously explained):
- ♪ In odd cases: We get the Magic Figure-2 in the esoteric magic squares by multiplying the central value of the box by 4
- ♪ In the case of the pair squares: We obtain the Magic Figure-2 with the sum of its 4 central squares (as is the case with the cross centers explained above in which to be taken 2).
That is, the 'specific weight' from the center remains in equilibrium. If we wanted to use a general formula, it would be this: the mean of the central cells * 4. Since the odd cases do not have a central cell as the only one, the smallest case that meets this condition should be considered, always being 4 cells.
It can be checked with the example of 7 cells above, or with the one of 3, etc.
Positional properties
By which an esoteric magic square is considered to be ordered when other conditions are also met that are slightly different in the squares of n-even than those of n-odd. (The same square, rotated or reflected, ceases to be ordered, although it does not cease to be esoteric.
- n-impar: Nb occupies the central lodge. The higher number is above the central square and the lower one below. The corner r is occupied by the Nb-(n/2-(1/2) and the opposite or by the Nb+(n/2-(1/2) figure). The corner is occupied by the number n/2+(1/2) and the opposite box t, by 2×Nb- (the figure of s), or what is equal, by the greater number of the magic square, - (n/2-(1/2)).
- Diagonals: The diagonal that runs from the upper left corner to the lower right corner always carries its squares numbered correlatively. The other diagonal carries its numbered boxes in jumps of n starting just by (n +1)/2
- n-par: The square r (the 1.a), is occupied by number n, number 1 occupies the square s, and the last number, the diagonal t, and the locker u=t+s-r. Being pair, there is no central square, and Nb itself is not whole, and it does not occupy square.
- Diagonals: the one diagonal carries the numbered boxes in jumps of n-1 starting with n and the other diagonal carries the numbered boxes in jumps of n +1 starting with 1 and end up in n2.
Properties of Diagonals (Diametrals)
It is verified that the sum of two diametrically opposite cells always adds up to n² + 1. It applies equally to the cases of n=odd as to the cases of n=even, being only different, that for the odd case the center is a cell and for the even case there is no cell defined
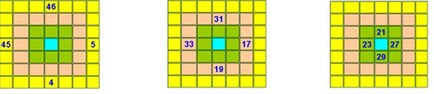
- In order not to saturate your check, only four examples are illustrated. a, b, c, d with its corresponding diametrically opposite to the center (which has been left on purpose).
- It can be verified with the values of the square on the right. Being: DI= n2 + 1= 72 + 1= 50 shows that: a DI= 47 + 3= 50, b DI=42 + 8= 50, c DI=6 + 44= 50, stop d DI=31 + 19= 50...
| - | a | - | - | - | - | 04 |
| - | - | - | - | b | 11 | - |
| - | c | - | - | 18 | - | - |
| - | d | - | 25 | - | d | - |
| - | - | 32 | - | - | c | - |
| - | 39 | b | - | - | - | - |
| 46 | - | - | - | - | a | - |
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
It can then be seen that the corner property is a natural consequence of this. This property together with the positional properties provide all the rules needed to build a general formula for making esoteric magic squares of any size which is covered a bit further down.
Allusions to Kabbalah
- There are equivalences between the figures of the esoteric magical squares and the letters of the Hebrew alphabet, considered by the cabalists, so that only when applied to the proper square, the cabalistic result can be correctly taken, the conclusions being inaccurate if the wrong magic square is taken.
The particular rules, as well as this general one, have been unknown by many who throughout time have tried to unravel their mysteries or unmask their lies, which is why the studies of those who ignored such issues lack validity., since the word took the number according to the rules of this to interpret the word, and not the word became a number to interpret the word, as such they intended. Just as words had their rules, so did numbers, and that was how their interpretation became sacred, for it was not enough to know numbers if you did not know their rules, just as it is not enough to understand a language, even if you know it. know their letters, if their rules are unknown....
- It is to be noted that however, despite the above mentioned in the article, those mentioned as Satanic squares, strictly in esoteric sense, are not taken by such if not only the square of side 6 esoteric, since the sum of their figures (Composition), sum 666. And it is where the cabalists seek or should seek the number of the Beast as mentioned in the Bible.
Making esoteric magic squares
- The process of developing esoteric magical squares is addressed in 2 phases. as seen throughout the article, cases of n par or impar carry situations that require different treatment.
- From the entrance and by abbreviation we agreed to call each diagonal with the following symbols: direct diagonal (left up to the right) with which we will call it d . Reverse diagonal (right up to the left) we will call it d/
- List of figures: to better recognize the change in each step has cleared the square of everything not necessary to understand the passage, for that reason at each step it is not necessarily accumulated the values already obtained.
Odd case
To explain how to make an esoteric magic square with an odd side, we previously decided n which for the example will be 9
- Being n=9 we calculate the number of boxes n2=9*9=81 and in turn we calculate NB with any of the formulas that were given before, the case NB = (n2+1) /2=41. NB it does not need to be calculated at this moment, however it serves to verify that it is a magical esoteric square and not another one.
| FI | GU | RA | AA | AA | AA | AA | AA | 01 |
| - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - |
| - | - | - | - | 81 | - | - | - | - |
| - | - | - | - | 41 | - | - | - | - |
| - | - | - | - | 1 | - | - | - | - |
| - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - |
| FI | GU | RA | AA | AA | AA | AA | AA | 02 |
| - | - | - | - | - | - | - | - | 5 |
| - | - | - | - | - | - | - | 14 | - |
| - | - | - | - | - | - | 23 | - | - |
| - | - | - | - | 32 | - | - | - | |
| - | - | - | - | 41 | - | - | - | - |
| - | - | - | 50 | - | - | - | - | |
| - | - | 59 | - | - | - | - | - | - |
| - | 68 | - | - | - | - | - | - | - |
| 77 | - | - | - | - | - | - | - | - |
- It shows the empty square and where the values will go 1, NB and n2 as indicated in positional properties above in the article. (see figure-1). The strategic importance of NBused in step-3
- Step 1: develop the main diagonal; d/ as indicated in positional properties: we calculate the first number: = (n + 1) /2 = 9 +1 /2=5 first value therefore 5, the following will be (no row-1) * n) + 1st row value case of row 2= ((2-1) * 9) +5=14, successively applying the same calculation will be: 23,32,41,50,59,68 and 77 (see figure-2).
The 1st image (figure-8) to the right of figure 7 shows a quick method of filling in both diagonals without the need to calculate.
| FI | GU | RA | AA | AA | AA | AA | AA | 03 |
| - | - | - | - | - | - | - | - | 5 |
| - | - | - | - | - | - | - | 14 | - |
| - | - | - | - | - | - | 23 | - | - |
| - | - | - | - | 32 | - | - | - | |
| - | - | - | - | 41 | - | - | - | - |
| - | - | - | 50 | 42 | - | - | - | |
| - | - | 59 | - | - | - | 43 | - | - |
| - | 68 | - | - | - | - | - | 44 | - |
| 77 | - | - | - | - | - | - | - | 45 |
| FI | GU | RA | AA | AA | AA | AA | AA | 04 |
| ♪ | - | - | - | - | 5 | |||
| - | 38 | - | - | - | 14 | - | ||
| - | 39 | - | - | 23 | - | |||
| - | - | 40 | 32 | - | - | |||
| - | - | 41 | - | - | ||||
| - | - | 50 | 42 | - | - | |||
| - | 59 | - | 51 | - | 43 | - | ||
| - | 68 | - | 60 | - | 52 | - | 44 | - |
| 77 | - | 69 | - | 61 | - | 53 | - | 45 |
- Step 2: elaborate diagonals on the main; all d that lead to d/ has correlative values therefore, starting with the central square downwards will be: 42,43,44,45 (figure-3) and upwards will be: 40,39,38,37... proceed equally from the rest of the boxes that form d/. With this we already have solved half the square, all odd boxes... (figure-4). In order not to enturb the figure-4, only a few boxes are filled and the other affected ones are marked with the same background color as these...
It can be seen in the image (figure-9) (the 2nd one to the right of figure-7, below), which cells are these, taken from the original square from which the values are taken, and which are the case correlatives. Observe the 45º rotation of the image to see the agreement clearly. The image illustrates the need to calculate these boxes. For example, for the first row, it can be seen that these are: 37 - 29 - 21 - 13 and 5.
| FI | GU | RA | AA | AA | AA | AA | AA | 05 |
| 37 | - | 29 | - | 21 | - | 13 | - | 5 |
| - | 38 | - | 30 | - | 22 | - | 14 | - |
| 47 | - | 39 | - | 31 | - | 23 | - | 15 |
| - | 48 | - | 40 | 32 | - | 24 | - | |
| 57 | - | 49 | - | 41 | - | 33 | - | 25 |
| - | 58 | - | 50 | 42 | - | 34 | - | |
| 67 | - | 59 | - | 51 | - | 43 | - | 35 |
| - | 68 | - | 60 | - | 52 | - | 44 | - |
| 77 | - | 69 | - | 61 | - | 53 | - | 45 |
| FI | GU | RA | AA | AA | AA | AA | AA | 06 |
| - | 29 | 70 | - | - | ||||
| - | - | - | - | - | ||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| 17 | 41 | - | ||||||
| - | 58 | - | - | 34 | - | |||
| - | 10 | 51 | - | 75 | ||||
| - | - | - | - | - | ||||
| - | - | - | - |
- Step 3: From this moment you have to consider the square in 4 zones, first in 2 separated by d/ and again divide each area into 2 according to d (see figure-5 where we paint each area of a color (only the missing box)). Each of the 4 delimited areas is resolved with sum or subtract of an existing value in the adhyacente box operating with NB, being conditioned each zone to the following criterion; The value of each box results from operating the immediate box next to the side:
- In the area North, left + NB
- In the area South, Right - NB
- In the area West, lower - NB
- In the area this, superior + NB. This is, a box in the area this is calculated adding the value of which is above this + NB.
The last image (3rd to the right of figure-7) shows where these cells come from in the original square, and how they are located in each sector. Compare each sector with the location of figure-9. It can be seen how the sectors have been moved. All the cells correspond to those shown in figure-7 in yellow.
- Only one box has been calculated in each area (see figure-6), to appreciate more clearly each case, for example, the area this. Take (see figure-5) the box between the one that has the value 34 and the one that has value 44, will be worth, which is worth the box as indicated by the area to which it corresponds, this case the one above it + NB= 34 + 41=75 (see figure-6 and check with figure-7).
Figure-7 shows the square completely filled in and the squares obtained in each step of the same color. The following colors correspond to each step: step 1: brown, step 2: sand, step 3: yellow. On the right is an image where the boxes that correspond to the diagonals are listed without the need to calculate. Note that the square in the image (figure 8) has all its boxes correlatively numbered from 1 to 81.
| FI | GU | RA | AA | AA | AA | AA | AA | 07 |
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5 |
| 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46 |
| 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15 |
| 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56 |
| 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25 |
| 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66 |
| 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35 |
| 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76 |
| 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45 |
Even case
- The methods explained in detail are valid for whatever number nwhich for space reasons has been worked with examples n It is easily manageable.
- When the rules are already known, they can be built according to another criterion based on the relationship between them. However, it is recommended to follow the instructions when done manually.
- Once a magical esoteric square is made it can easily move into any other type of magical square simply by substitution, addition, twist or any other method.
Magic Squares in Popular Culture
- In the Fausto (Goethe)The witch's rabble to make the youth elixir for Fausto has been interpreted as the construction of a magical square.
- On October 9, 2014, Macao's mail in the People's Republic of China issued a series of postage stamps based on magical squares.
- An episode of the first season Stargate Atlantis involves completing a magical square as part of a puzzle to access a powerful ancient amulet.
- The novel The Seven Fathers of Kimera includes two original magical squares, in addition to making reference to the square of Alberto Durero. In one of them, of 5x5, the broken diagonals have the magic sum (it is pandiagonal) and also the golden number appears approximately in several relationships. The other, 6x6, in addition to including numbers related to the book's plot, serves to solve a puzzle in the appendix.
Contenido relacionado
Mathematical equality
Zero divisor
Closed and exact differential forms













![{displaystyle M_{2}(n)={frac {n[2a_{0}+(n^{2}-1)r]}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12a02d1b31ea3d4e468f43b92a6bdbb3c36709f)



