Mach number

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

An F/A-18 Hornet flying at supersonic speed. The white disk formed is water vapor condemning as a result of shock wave. This phenomenon is known as uniqueness of Prandtl-Glauert.

The Mach number (M), known in colloquial use as mach, is a measure of relative speed that is defined as the ratio between the speed of an object and the speed of sound in the medium in which said object moves. This relationship can be expressed according to the equation:

${displaystyle mathrm {M} ={frac {u}{u_{s}}}}$
Symbol	Name
${displaystyle mathrm {M} }$	Number Mach
$u$	Speed of moving object
${displaystyle u_{s}}$	Sound speed in the physical environment

It is a dimensionless number normally used to describe the speed of aircraft. Mach 1 equals the speed of sound, Mach 2 is twice the speed of sound, and so on.

This number was proposed by the Austrian physicist and philosopher Ernst Mach (1838-1916), one of the greatest physics theorists of the 19th-20th centuries, as a simple way of expressing the velocity of an object with respect to at the speed of sound.

The utility of the Mach number lies in the fact that it allows the speed of an object to be expressed not absolutely in km/h or m/s, but taking the speed of sound as a reference, something interesting since the speed of sound It changes depending on the conditions of the atmosphere. For example, the higher the altitude above sea level or the lower the temperature of the atmosphere, the lower the speed of sound. In this way, it is not necessary to know the speed of sound to know if an airplane flying at a given speed has exceeded it: it is enough to know its mach number.

From the point of view of fluid mechanics, the importance of the Mach number lies in its relationship with the compressibility of a gas; when this number is less than 0.3, it is considered an incompressible fluid in the study of aerodynamics and models with air or gases, greatly simplifying the calculations made by computer.

General information

Mach is commonly used with objects moving at high speed in a fluid, and in the study of rapidly flowing fluids inside nozzles, diffusers, or wind tunnels. At a temperature of 15 °C, Mach 1 is equal to 340.3 m/s (1,225 km/h) in the atmosphere. The Mach number is not a constant since it depends on the temperature. Therefore, in the stratosphere it does not vary appreciably with height, even when the air pressure changes with height.

This number is widely used in aeronautics to compare the behavior of fluids around an aircraft under different conditions. This is possible thanks to the fact that the behavior of a fluid in the environment of an object is the same as long as its Mach number is the same. Therefore, an aircraft traveling at Mach 1 will experience the same shock waves regardless of whether it is at sea level (340.3 m/s, 1,225,080 km/h) or 11,000 meters altitude (295 m). /s, 1062 km/h), even when in the second case its speed is 86.7% of that of the first case.

The classification of the regimes including the hypersonic regime is not capricious: for very high M (the technical frontier depends on the shape of the mobile, in general M>5), the shock waves are of such magnitude that the air is dissociates behind them, and ceases to be air, with the properties that are accepted in it, to become a mixture of dissociated gases, with electrically charged layers although neutral as a whole, which stops behaving as air did.

It is shown that the Mach number is also the quotient of the inertial forces (also referring to the aerodynamic forces) and the elastic forces.

Flow at high speed around an object

Normally, flight speeds are classified according to their Mach number in:^{[citation needed]}


Values	Description
M ≥ 0.7	Subsonic
0.7 ≤2	Transonic
1.2.	Supersonic
M  5	Hypersonic

For comparison, the speed required to reach a low Earth orbit is about 7.5 km/s = Mach 25.4 in air at high altitudes.


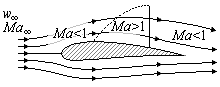(a)	(b)

Fig. 1. Mach number in the transonic airflow around an airfoil; Ma < 1(a) and Ma > 1(b)

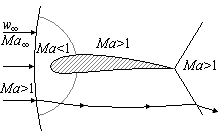
At transonic speeds, the flow field around the object includes sub and supersonic parts. The transonic regime begins when the first Ma>1 flow zones appear around the object. In the case of an airfoil (such as an airplane wing), this usually occurs above the wing. The supersonic flow can decelerate back to subsonic only in a normal shock; this typically occurs before the trailing edge. (Fig.1a)

As speed increases, the flow zone Ma>1 increases towards the leading and trailing edges. When Ma=1 is reached and passed, the normal shock reaches the trailing edge and becomes a weak oblique shock: the flow decelerates over the shock, but remains supersonic. A normal shock is created ahead of the object, and the only subsonic zone in the flow field is a small area around the leading edge of the object. (Fig.1b)


(a)	(b)

Fig. 1. Mach number in a transonic airflow over an airfoil; Ma<1 (a) and Ma>1 (b).

When an aircraft exceeds Mach 1 (ie the sound barrier) a large pressure difference is created right in front of the aircraft. This abrupt pressure difference, called a shock wave, propagates behind and out of the aircraft in a cone shape (the so-called Mach cone). This shock wave is what causes the sonic boom heard when a fast-moving aircraft passes overhead. A person inside the plane will not hear it. The higher the speed, the narrower the cone; at a little more than Ma=1 it is hardly a cone, but closer to a slightly concave plane.

At fully supersonic speed, the shock wave begins to take its cone shape, and the flow is fully supersonic, or (in the case of a blunt object), only a very small zone of subsonic flow remains between the nose of the object and the shock wave it creates ahead. (In the case of a sharp object, there is no air between the nose and the shock wave: the shock wave leaves the nose.)

As the Mach number increases, so does the force of the shock wave, and the Mach cone gets narrower and narrower. As the fluid flow passes through the shock wave, its velocity is reduced and the temperature, pressure, and density increase. The stronger the shock, the greater the changes. At sufficiently high Mach numbers, the temperature rises so much upon the shock that ionization and dissociation of the gas molecules behind the shock wave begins. These flows are called hypersonic.

Clearly, any object traveling at hypersonic speeds will be equally exposed to the same extreme temperatures as the gas behind the nose shock wave, so it's important to choose heat-resistant materials.

High speed flow in one channel

When a flow in a channel traversing M=1 becomes supersonic, a significant change occurs. Common sense would lead us to expect that the contraction of the flow channel would increase the velocity of the flow (i.e., by making the channel narrower the airflow is faster) and at subsonic speeds this is true. However, once the flow becomes supersonic, the relationship between flow area and velocity is reversed: widening the channel increases velocity.

The obvious result is that to accelerate a flow to the supersonic level requires a convergent-divergent nozzle, in which the convergent section accelerates the flow to M=1, sonic velocities, and the divergent section continues acceleration. These nozzles are called de Laval nozzle and in extreme cases are capable of reaching incredible, hypersonic speeds (Mach 13 at sea level).

An aircraft Mach gauge or Electronic Flight Information System (EFIS) can display Mach number derived from stagnation pressure (pitot tube) and static pressure.

Assuming that air is an ideal gas, the formula for computing the Mach number in subsonic compressible flow is derived from Bernoulli's equation for M <1:

{displaystyle {M}={sqrt {5{Bigg [}{bigg (}{frac {q_{c}}{P}}+1{bigg)}^{frac {2}{7}}-1{Bigg ]}}}}

where

M

is the number of Mach

{displaystyle q_{c}}

is the impact pressure and

P

It's static pressure.

The formula for calculating the Mach number in a supersonic compressible flow is obtained from the supersonic Rayleigh Pitot equation:

{displaystyle {M}=0.88128485{sqrt {{Bigg [}{bigg (}{frac {q_{c}}{P}}+1{bigg)}{bigg (}1-{frac {1}{[7M^{2}]}}{bigg)}^{2.5}{Bigg ]}}}}

where

M

is the number of Mach

{displaystyle q_{c}}

is the measured impact pressure behind the normal shock ind

P

It's static pressure.

Contenido relacionado

Más resultados...