Linked list
In computer science, a linked list is one of the fundamental data structures, and can be used to implement other data structures. It consists of a sequence of nodes, in which arbitrary data fields and one or two references, links, or pointers to the previous or subsequent node are stored. The main benefit of linked lists over conventional arrays is that the order of the linked elements can be different from the order in which they are stored in memory or on disk, allowing the traversal order of the list to be different from the order of storage.
A linked list is a self-referencing data type because it contains a pointer or link (in English link, of the same meaning) to another data of the same type. Linked lists allow insertion and deletion of nodes at any point in the list in constant time (assuming that point is previously identified or located), but do not allow random access. There are different types of linked lists: simple linked lists, doubly linked lists, circular linked lists, and circular doubly linked lists.
Linked lists can be implemented in many languages. Languages such as Lisp, Scheme, and Haskell have built-in data structures, along with operations to access linked lists. Imperative or object-oriented languages such as C or C++ and Java, respectively, have references to create linked lists.
History
Linked lists were developed in 1955-56 by Cliff Shaw and Herbert Simon at the RAND Corporation, as the main data structure for their Information Processing Language (IPL). IPL was used by the authors to develop various programs related to artificial intelligence, including the General Theory Machine, the General Problem Solver, and a chess computer program. It was published in IRE Transactions on Information Theory in 1956, and in various conferences between 1957-1959, including Proceedings of the Western Joint Computer in 1957 and 1958, and in Information Processing (From the first international conference of Unesco Information Processing) in 1959. The current classic diagram, consisting of blocks representing list nodes with arrows pointing to successive list nodes, appeared in Newell and Shaw's Programming the Logic Theory Machine. Newell and Simon were recognized by the ACM Turing Award in 1975 for "making basic contributions to artificial intelligence, the psychology of human knowledge, and list processing."
The problem of natural language processing translators led Victor Yngve of the Massachusetts Institute of Technology (MIT) to use linked lists as a data structure in his COMIT, a programming language for computers, which he did research in the field of computational linguistics. A report on this language, titled “A programming language for mechanical translation” appeared in Mechanical Translation in 1958.
LISP, the main list processor, was created in 1958. One of LISP's main data structures is the linked list.
By the 1960s, the utility of linked lists and languages that used these structures as their primary data representation were well established. Bert Green of MIT's Lincoln Laboratory published a study titled Computer languages for symbol manipulation in IRE Transaction on Human Factors in Electronics in March 1961 that summarized the advantages of linked lists. A later article, A Comparison of list-processing computer languages by Bobrow and Raphael, appeared in Communications of the ACM in April 1964.
Many operating systems developed by Technical Systems Consultants (originally of West Lafayette Indiana and later of Raleigh, North Carolina) used simple linked lists as file structures. An input directory pointed to the first sector of a file and returned portions of the file's location as pointers. Systems using this technique included the Flex (for the Motorola 6800 CPU), mini-Flex (same CPU), and Flex9 (for the Motorola 6809 CPU). A variant developed by TSC was marketed to Smoke Signal Broadcasting in California, using doubly linked lists in the same way.
The TSS operating system, developed by IBM for the System 360/370 machines, used a doubly linked list for its catalog of system files. The directory structure was similar to Unix, where a directory could contain files or other directories that could extend to any depth. A utility was created to fix system problems after a crash from the modified portions of the fileset that were sometimes in memory when the crash occurred. Problems were detected by comparing the back and back links for consistency. If the next one was corrupted and the previous link of the infected node was found, the next link was assigned to the node marked with the previous link.
Types of linked lists
Simple linked lists
It is a linked list of nodes, where each node has a unique link field. A reference variable contains a reference to the first node, each node (except the last) links to the next node, and the last node's link contains NULL to indicate the end of the list. Although the reference variable is usually called top, it could be called anything you like.

A simply linked list containing three whole values
Doubly Linked Lists
A more sophisticated type of linked list is the doubly linked list or two-way linked list. Each node has two links: one points to the previous node, or points to NULL if it is the first node; and another that points to the next node, or points to the NULL value if it is the last node.
In some very low-level languages, XOR-Linking offers a way to implement doubly linked lists, using a single word for both links, although this technique is rarely used.

A double-linked list containing three whole values
Circular Linked Lists
In a circular linked list, the first and last nodes are joined together. This can be done for both single and doubly linked lists. To traverse a circular linked list we can start at any node and follow the list in any direction until we return to the original node. From another point of view, circular linked lists can be seen as lists without beginning or end. This type of list is the most used to direct buffers to "ingest" data, and to visit all the nodes of a list starting from a given one.

A circular linked list containing three whole values
Simple circular linked lists
Each node has a link, similar to simple linked lists, except that the next node from the last points to the first. As in a simple linked list, new nodes can only be efficiently inserted after one we already have referenced. For this reason, it is usual to stick with a reference to only the last element in a simple circular linked list, this allows for quick insertions at the beginning, and also allows access to the first node from the last node pointer.
Doubly circular linked lists
In a circular doubly linked list, each node has two links, similar to a doubly linked list, except that the previous link from the first node points to the last node, and the next link from the last node points to the first. As in a doubly linked list, insertions and deletions can be done from any point with access to a nearby node. Although structurally a circular doubly linked list has neither beginning nor end, an external access pointer can set the head node or the tail node pointed to, and thus maintain order just as well as in a doubly linked list.
Sentinel nodes
Sometimes linked lists have a sentinel node (also called dummy node or dummy node) at the beginning or end of the list, which is not used to store data. Its purpose is to simplify or speed up some operations, ensuring that any node has a previous or a subsequent one, and that the entire list (even one that does not contain data) always has a “first and last” node.
Applications of Linked Lists
Linked lists are used as modules for many other data structures, such as stacks, queues, and their variations.
The data field of a node can be another linked list. Using this mechanism, we can build many data structures linked to lists; this practice originates from the Lisp programming language, where linked lists are a primary (though not the only) data structure, and is now a common feature in the functional programming style.
Sometimes, linked lists are used to implement associative vectors, and these are in the context of so-called associative lists. There are few advantages to this use of linked lists; there are better ways to implement these structures, for example with balanced binary search trees. However, sometimes a linked list is dynamically created out of a proper tree-like subset of nodes, and they are used more efficiently to traverse this data series.
Advantages
Like many choices in programming and development, there is no single correct method for solving a problem. A linked list structure may work well in one case but cause problems in others. Here is a list of some of the more common benefits of list-like structures. In general, having a dynamic collection where items are being added and removed frequently and the location of newly introduced items matters increases the benefit of linked lists.
Linked Lists vs. vectors or matrices
| Vector | Linked list | |
|---|---|---|
| Indexed | O(1) | O(n) |
| Insertion / Removal at the end | O(1) | O(1) or O(n) |
| Insertion / Elimination in half | O(n) | O(1) |
| Persistence | No. | Simple yes |
| Locality | Good. | Bad |
Linked lists have many advantages over vectors. Elements can be inserted into a list indefinitely whereas an array will sooner or later fill up or need to be resized, an expensive operation that may not even be possible if memory is fragmented.
In some cases memory savings can be achieved by storing the same 'tail' of elements between two or more lists - that is, the list ends in the same sequence of elements. In this way, one can add new elements to the front of the list by keeping a reference to both the new and the old elements - a simple example of a persistent data structure.
On the other hand, vectors allow random access while linked lists only allow sequential access to elements. Simple linked lists can, in fact, only be traversed in one direction. This makes lists unsuitable for cases where it is useful to quickly look up an element by its index, such as heapsort. Sequential access on arrays is also faster than on linked lists.
Another disadvantage of linked lists is the extra storage needed for references, which often make them impractical for lists of small data such as characters or boolean values.
It can also be slow and abusive to allocate memory for each new element. There are a variety of linked lists that contemplate the above problems to solve the same. A good example that shows the pros and cons of using vectors on linked lists is the implementation of a program that solves Flavio Josefo's problem. This problem consists of a group of people arranged in a circle. It starts from a predetermined person and is counted n times, the nth person is removed from the circle and the group is closed again. This process is repeated until there is only one person left, who is the one who wins. This example shows the strengths and weaknesses of linked lists versus vectors, since seeing people as nodes connected to each other in a circular list makes it easier to suppress these nodes. However, you can see how the list will lose its usefulness when you have to find the next person to delete. On the other hand, in a vector, removing the nodes will be expensive since you cannot remove one element without rearranging the rest. But in the search for the nth person, it is enough to indicate the index n to access it, resulting in much more efficiency.
Doubly linked vs. simply linked
Doubly linked lists require more space per node and their basic operations are more expensive, but they are easier to manipulate since they allow sequential list access in both directions. In particular, one can insert or delete a node in a fixed number of operations by giving only the address of that node (Simple lists require the address of the previous node to insert or delete correctly). Some algorithms require access in both directions in order to acquire the linked lists.
Linked circulars vs. linked linear
Circular lists are most useful for describing circular structures and have the advantage of being able to traverse the list from any point. They also allow quick access to the first and last element by means of a simple pointer.
Sentinel nodes (header nodes)
The common search and sorting algorithms are less complicated if so-called Sentinel Nodes or Dummy Nodes are used, where each element points to another element and never to null. The Sentinel Node or Head Pointer contains, like another, a next pointer that points to what is considered the first element of the list. It also contains a previous pointer that does the same for the last element. The Sentinel Node is defined as another node in a doubly linked list, front pointer assignment is not necessary and the previous and next pointers will be pointing to itself at that time. If the previous and next pointers point to the Sentinel Node the list is considered empty. Otherwise, if elements are added to the list, both pointers will point to other nodes. These Sentinel Nodes simplify operations a lot but you have to make sure that the previous and next pointers exist at all times. As an advantage, they eliminate the need to store the reference to the pointer to the beginning of the list and the possibility of accidental assignments. On the contrary, they use too much extra storage and are cumbersome in some operations.
Linked lists using node vectors
Languages that do not accept any type of reference can create unions by replacing pointers with indices of an array. The advantage is to maintain a vector of entries, where each entry has integer fields indicating the index of the next element of the vector. There may be unused nodes. If there is not enough space, parallel vectors can be used.
Then a linked list can be constructed, an array created with this structure, and an integer variable to store the index of the first element. (see in the implementations section).
The utilities of this proposal are:
- The linked list can be moved on memory and also be quickly serialized to store it on a disk or transfer it on a network.
- Especially for a small list, indexed vectors can occupy much less space than a set of pointers.
- The reference location can be improved by keeping the nodes together in memory and being reordered periodically.
Some disadvantages are:
- It increases the complexity of implementation.
- Using a general memory fund leaves more memory for other data if the list is smaller than expected or if many nodes are released.
- The growth of a vector when it is full cannot take place (or it should be redimensed) while finding space for a new node on a list is possible and easier.
For these reasons, the proposal is mainly used for languages that do not support dynamic memory allocation. These drawbacks are also mitigated if the maximum size of the list is known at the time the array is created.
Supported languages
Many programming languages such as Lisp and Scheme have simple linked lists already built. In many programming languages, these lists are built by nodes, each called a cons or cons cell. Cons cells have two fields: char, a data reference to the node, and cdr, a reference to the next node. Although cons cells can be used to build other data structures, this is their main purpose.
In languages that support abstract data types or templates, linked list ADTs or templates are available for constructing linked lists. In other languages, linked lists are typically constructed using references along with the record data type.
In the implementations section there is a complete example in C and in Maude
Internal and external storage
When building a linked list, we are faced with the choice of whether to store the list data directly in the linked list nodes, called internal storage, or simply store a reference to the data, called external storage. Internal storage has the advantage of making data access more efficient, requiring less global storage, having better locality reference, and simplifies memory management for the list (data is allocated and evicted at the same time as nodes in the list). list).
External storage, on the other hand, has the advantage of being more generic, in that the same data structure and machine code can be used for a linked list, no matter what its size or data. This makes it easier to put the same data in multiple linked lists. Although with internal storage the same data can be placed in multiple lists by including multiple next references in the node's data structure, this might then be necessary to create separate routines to add or delete cells based on each field. This is possible by creating additional linked list items that use internal storage using external storage, and having the cells of the additional linked lists store the references to the linked list nodes that contain the data.
In general, if a series of data structures need to be included in multiple linked lists, external storage is the best approach. If a number of data structures need to be included in a single linked list, then internal storage is slightly better, unless a generic list package using external storage is available. Also, if different data sets that can be stored in the same data structure are included in a single linked list, then internal storage may be better.
Another approach that can be used with some languages involves having different data structures, but all have the initial fields, including the next (and previous if a doubly linked list) reference in the same location. After defining separate structures for each data type, a generic structure can be defined to contain the minimum amount of data shared by all structures and contents at the beginning of the structures. Then generic routines can be created using the minimal structures to carry out the operations of the linked list types, but separate routines that can handle the specific data. This approach is often used in message parsing routines, where several types of messages are received, but all start with the same set of fields, usually including a field for the type of message. Generic routines are used to add new messages to a queue when they are received, and remove them from the queue in order to process them. The message type field is used to call the correct routine to process the specific type of message.
In the implementations section (in this same article) code regarding this topic is exposed.
Note that when using external storage, an extra step needs to be taken to extract the node information and cast it into the data type itself. This is because both family and member lists are stored in two linked lists using the same data structure (node), and this language has no parametric types.
If we know the number of families a member can belong to at compile time, internal storage works best. If, however, a member needs to be included in an arbitrary number of families, knowing the specific number of families only at runtime, external storage will be necessary.
Search streamlining
Finding a specific element in a linked list, even if it is sorted, usually requires O(n) time (linear search). This is one of the main disadvantages of linked lists compared to other structures. In addition to some of the variants discussed in the previous section, there are numerous simple ways to improve seek time.
In an unordered list, a simple way to decrease the average seek time is the move-to-front heuristic, which simply moves an item to the top of the list once it's found. This idea, useful for creating simple caches, ensures that the most recently used item is also the fastest to be found again.
Another common approach is to index a linked list using a more efficient external data structure. For example, we can build a red-black tree or a hash table whose elements are referenced by the nodes of the linked lists. Multiple indices can be built on a single list. The downside is that these indices may need to be updated every time a node is added or removed (or at least before the index is used again).
Related data structures
Both stacks and queues are often implemented using linked lists, and simply restricting the type of operations that are supported.
The skip list is a linked list augmented with layers of pointers for quickly jumping over large numbers of elements, and descending to the next layer. This process continues until the bottom layer is reached, which is the current list.
A binary tree can be seen as a type of linked list where the elements are linked to each other in the same way. The result is that each node can include a reference to the first node of one or two linked lists, each with its contents, thus forming the subtrees under the node.
An unrolled linked list is a linked list whose nodes contain a data vector. This improves cache performance, as long as the lists of items are contiguous in memory, and reduces memory overhead, because you need less metadata to save each list item.
A hash table can use linked lists to store strings of items at the same position in the hash table.
Implementations
Here the necessary code is exposed to complement the article in order to be able to make an agile reading about the article and in turn whoever needs the code can easily find it if it is contained.
Operations on linked lists
When manipulating linked lists, be careful not to use values that you've overridden in previous assignments. This makes the algorithms for inserting and deleting nodes in lists somewhat special. The following is the pseudocode for adding and deleting nodes in single, double, and circular linked lists.
Linear Linked Lists
Simple linked lists
Our data structure will have two fields. We are going to keep the variable firstNode which always points to the first node of such a list, or null for the empty list.
record Node {
data // The data stored in the nodenext // A reference to the next node, zero for the last node!
record Ready. {
Node firstNote // Point to the first node of the list; void!
Traversal in a linked list is simple, we start at the first node and move to the next one until the list reaches the end.
node:= list.firstNodo
while node not null {
node:= node.next
!
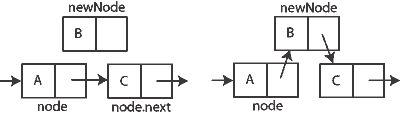
The following code inserts one element after another in a simple list. The diagram shows how it works.
function insert(Node Node, Node newNode) {
newNode.next:= node.next
node.next:= newNode
!
Inserting at the beginning of a list requires a separate function. FirstNode needs to be updated.
function insertBeginning()Ready. list, Node newNode) {
newNode.next:= list.firstNode
list.firstNode:= newNode
!
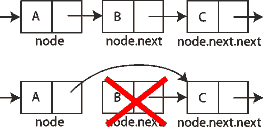
Similarly, we also have functions to delete a given node or to delete a node from the top of the list. See diagram.
function remove(Node node) {
obsoleteNode:= node.next
node.next:= node.next.next
destroy obsoleteNode
!
function removeBeginning()Ready. list) {
obsoleteNode:= list.firstNode
list.firstNode:= list.firstNode.next
destroy obsoleteNode
!
Note that DeleteBeginning sets FirstNode to null when the last item in the list is deleted. Attaching one linked list to another can be inefficient unless a reference to the list's tail is stored, otherwise we would have to iterate through the list in order to reach the tail and then add the second list.
Doubly Linked Lists
With these lists, many more pointers need to be updated but also less information is needed because we can use a pointer to traverse back and query items. New operations are created and some special cases are removed. We add the previous field to our nodes, pointing to the previous item, and lastNode to our structure, which always points to the last item in the list. firstNode and lastNode are always null on the empty list.
record Node {
data // The data stored in the nodenext // A reference to the next node, zero for the last nodeprev // A reference to the previous node, zero for the first node!
record Ready. {
Node firstNode // points to the first node of the list; void Node lastNode // points to the last node of the list; nose for the empty list!
Ways of traversing the list:
Forward
node:= list.firstNode while I don't. null≥do something with node.data node:= node.next
Backward
node:= list.lastNode while I don't. null≥do something with node.data node:= node.prev
These symmetric functions add a node after or before a given one:
function insert(Ready. list, Node Node, Node newNode) newNode.prev:= node newNode.next:= node.next if Node.next = nullnode.next:= newNode list.lastNode:= newNode elsenode.next.prev:= newNode node.next:= newNode
function insertBefore()Ready. list, Node Node, Node newNode) newNode.prev:= node.prev newNode.next:= node if node.prev is null node.prev:= newNode list.firstNode:= newNode elsenode.prev.next:= newNode node.prev:= newNode
We also need a function to insert a node at the beginning of a possibly empty list.
function insertBeginning()Ready. list, Node newNode) if list.firstNode = nulllist.firstNode:= newNode list.lastNode:= newNode newNode.prev:= null newNode.next:= null elseinsertBefore (list, list.firstNode, newNode)
A symmetric function that inserts at the end:
function insertEnd()Ready. list, Node newNode) if list.lastNode = nullinsertBeginning (list, newNode) elseinsertAfter (list, list.lastNode, newNode)
Deleting a node is easy, it just requires careful use of firstNode and lastNode.
function removeReady. list, Node node) if node.prev = nulllist.firstNode:= node.next elsenode.prev.next:= node.next if Node.next = nulllist.lastNode:= node.prev elsenode.next.prev:= node.prev destroy node
A special consequence of this procedure is that deleting the last element of a list sets FirstNode and LastNode to null, thus creating a problem with a list that has only one element.
Circular Linked Lists
These can be single or doubly linked. In a circular list all nodes are linked as a circle, without using null. For lists with front and end (such as a tail), a reference to the last node in the list is stored. The next node after the last one would be the first one in the list. Elements can be added at the end and deleted at the beginning at any time. Both types of circular lists have the advantage of being fully traversable starting from any node. This allows us to normally avoid using FirstNode and LastNode, although if the list were empty we would need a special case, such as a variable LastNode that points to some node in the list or null if it is empty. The operations for these lists simplify inserting and deleting nodes in an empty list but introduce special cases in the empty list.
Doubly circular linked lists
Assuming that someNode is some node in a non-empty list, this list presents the beginning of a list with someNode.
Forward
node:= someNode dodo something with node.value node:= node.next while node!
Backward
node:= someNode dodo something with node.value node:= node.prev while node:= someNode
This function inserts a node into a circular doubly linked list after a given element:
function insert(Node Node, Node newNode) newNode.next:= node.next newNode.prev:= node node.next.prev:= newNode node.next:= newNode
To do "insertBefore", we can simplify "insertAfter (node.prev, newNode)". Inserting an item into a list that may be empty requires a special function.
function insertEnd()Ready. list, Node node) if list.lastNode = nullnode.prev:= node node.next:= node elseinsertAfter (list.lastNode, node) list.lastNode:= node
To insert at the beginning we simplify "insertAfter (list.lastNode, node)".
function removeReady. list, Node node) if node.next = node list.lastNode:= null elsenode.next.prev:= node.prev node.prev.next:= node.next if node = list.lastNode list.lastNode:= node.prev; destroy node
As a doubly linked list, "removeAfter" and "removeBefore" can be implemented with "remove (list, node.prev)" and "remove(list, node.next)".
Linked lists using node vectors
Previously, a structure containing the pointers is created:
record Entry {
integer next; // New entry index in the vector integer prev; // Previous entry string name;
Real balance;
!
And finally the vector is declared: integer listHead;
Entry Records[1000];
Implementation of a linked list in C
Linked lists are typically constructed using references along with the record data type.
# Include ≤2.h /* for printf */# Include ≥stdlib.h /* for malloc */typedef struct ns {int data;struct ns ♪next;! node;node ♪list_add(node **p, int i) { /* some compilers do not require a return value casting for malloc */ node ♪n = (node ♪)malloc(sizeof(node)); if (n ♪ NULL) return NULL; n- 2005next = ♪p; ♪p = n; n- 2005data = i; return n;!void list_remove(node **p) { ♪ Delete head ♪ if (♪p = NULL) { node ♪n = ♪p;♪p = (♪p)- 2005next;free(n); !!node **list_search(node **n, int i) { while (♪n = NULL) { if (♪n)- 2005data ♪ i) { return n; ! n = "(♪n)- 2005next; ! return NULL;!void list_print(node ♪n) { if (n ♪ NULL) { printf("listen is emptyn"); ! while (n = NULL) { printf("print %p %p %dn", n, n- 2005next, n- 2005data); n = n- 2005next; !!int main(void) { node ♪n = NULL; list_add("n, 0); /* list: 0 */ list_add("n, 1); /* list: 1 0 */ list_add("n, 2); /* list: 2 1 0 */ list_add("n, 3); /* list: 3 2 1 0 */ list_add("n, 4); /* list: 4 3 2 1 0 */ list_print(n); list_remove("n); /* delete first(4) */ list_remove("n- 2005next); /* delete new second (2) */ list_remove(list_search("n, 1)); /* remove the cell containing 1 (first) */ list_remove("n- 2005next); /* remove second end node(0)*/ list_remove("n); /* remove last node (3) */ list_print(n); return 0;!Implementation of a simply linked list in C++ using classes
Simply linked lists using pointers and memory addresses. In this example we use two classes: a class TElemento (node, item or element) and a class TlistaSL (simply linked, or simply linked). Each one of them with its attributes and methods pointing to Info (element information) and aSeguinte (pointer to the next element) as the most important.
//--Unit2.h-----------------------------------------------------------#ifndef Unit2H#define Unit2H# Include أعربية//--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------class I'm sorry.{protected: int aInfo; I'm sorry. ♪aSeguinte ;public: I'm sorry.(int pInfo♪aInfo = pInfo; aSeguinte=NULL; //Builder ~I'm sorry.(){}; //Destroyer //Operações int LerInfo(){return aInfo; //Ler void EscInfo(int pInfo♪aInfo = pInfo; //Screver I'm sorry. ♪LerSeguinte(){return aSeguinte; //Ler void EscSeguinte(I'm sorry. ♪pSeguinte♪aSeguinte = pSeguinte; //Screver};class TListaSL{private: I'm sorry. ♪aPrimeiro; int along;public: TListaSL(){aPrimeiro = NULL; along = 0; //Builder TListaSL(int pnovoelement); //Builder ~TListaSL(); //Destroyer //Operações int Length(){return along; Bool Vazia(){return !along; void Accreditation(int pnovoelement); void Insert(int pnovoelement, int p.); void Delete(int p.); int Obter(int p.); void Show();};#endif//--Final Unit2.h---------------------//--Unit2.cpp--------------------------------------------------------------------------------------------#pragma hdrstop# Include "Unit2.h"# Include Δvcl.h#pragma argsused//--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------TListaSL::TListaSL(int pnovoelement♪ aPrimeiro = new I'm sorry.(pnovoelement); along = 1;!TListaSL::~TListaSL(){ I'm sorry. ♪cursor; while(aPrimeiro♪ cursor = aPrimeiro; cursor = aPrimeiro- 2005LerSeguinte(); Delete cursor; !!void TListaSL::Accreditation(int pnovoelement♪ I'm sorry. ♪Novo = new I'm sorry.(pnovoelement); if (Vazia()) aPrimeiro = Novo; else{ I'm sorry. ♪cursor = aPrimeiro; while(cursor- 2005LerSeguinte()) cursor = cursor- 2005LerSeguinte(); cursor- 2005EscSeguinte(Novo); ! along+;!void TListaSL:: Delete(int p. ♪ if (p..0) 日本語 (p.▪along) printf("n Nao elimino. Posicao fora rank"); // Posiçao fora a rank I'm sorry. ♪cursor = aPrimeiro; if (p. = 0♪ for (int i = 0; i . p. - 1; i+♪ cursor = cursor- 2005LerSeguinte(); ! I'm sorry. ♪# I'm sorry # = cursor- 2005LerSeguinte(); //referência ao nodo cursor- 2005EscSeguinte(# I'm sorry #- 2005LerSeguinte()); // pulling gives list cursor = # I'm sorry #; ! else // Remove or primeiro nodo aPrimeiro= aPrimeiro- 2005LerSeguinte(); Delete cursor; along--;!void TListaSL::Insert(int pnovoelement, int p.♪ if (p..0) 日本語 (p. ▪ along) printf("n Nao insiriou. Posicao fora rank"); //Posiçao fora a rank I'm sorry. ♪Novo = new I'm sorry.(pnovoelement); if (p. = 0♪ I'm sorry. ♪cursor = aPrimeiro; int counter = 1; while (counter . p.♪ cursor = cursor- 2005LerSeguinte(); // Positioning-not prior node counter+; ! Novo- 2005EscSeguinte(cursor- 2005LerSeguinte()); cursor- 2005EscSeguinte(Novo); ! else { Novo- 2005EscSeguinte(aPrimeiro); //Inserir na primeira posição aPrimeiro = Novo; ! along+;!int TListaSL::Obter(int p.♪ if (p..0) 日本語 (p.▪along) printf("n Nao posso show. Posicao fora rank"); //Posiçao fora a rank I'm sorry. ♪cursor = aPrimeiro; for (int i = 0; i . p.; i+♪ //Percorrer a lista até chegar ao element pIndice cursor = cursor- 2005LerSeguinte(); ! return cursor- 2005LerInfo();!void TListaSL::Show(){ I'm sorry. ♪cursor = aPrimeiro; for(int i = 0; i ♫ along - 1; i+♪ printf("%i", cursor- 2005LerInfo()); cursor = cursor- 2005LerSeguinte(); !!/* Major implementation programme with some test operations */int main(int argc, Char♪ argv[]{ Char Wait.; TListaSL ♪List = new TListaSL(); List- 2005Accreditation(0); List- 2005Accreditation(3); List- 2005Accreditation(2); List- 2005Accreditation(12); List- 2005Accreditation(6); List- 2005Accreditation(9); List- 2005Accreditation(7); printf("n List of elements: "); List- 2005Show(); //printf("n%i", List- PHPObter(3)); List- 2005Insert(20,2); printf("n List plus one inserted: "); List- 2005Show(); List- 2005Delete(6); printf("n List less one removed: "); List- 2005Show(); cin ◊ Wait.; return 0;};//--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------#pragma package(smart_init)Implementing a Linked List in C++
# Include ▪ // For cout# Include ▼ // Used to validate keyboard inputs# Include ▪ // Used to validate memory reservation when using the NEW operator.using namespace stdstruct camera_t { int idcam; string serial; int idroom; camera_t ♪next; };//Insert at the beginning of a list requires a separate function. FirstNote is needed.void list_add(camera_t **node_cam){ camera_t ♪newnode = new (Nothrow) camera_t; if(newnode♪NULL♪ cout ; "Error. Can't allocate memory to new node."; ! else{ newnode- 2005next = ♪node_cam; ♪node_cam = newnode; cout ; "Hello"; !!//The route on a linked list is simple, we begin by the first node and pass to the next// let the list come to the end.void list_print(camera_t ♪node_cam){ if (node_cam ♪ NULL♪ cout ; "Lista vacia"; ! else{ while (node_cam=NULL) { cout ; "idcam: " ; node_cam- 2005idcam ; "nName: " ; node_cam- 2005name ; "nModel: " ; node_cam- 2005model; cout ; "nSerial: " ; node_cam- 2005serial ; "nIdRoom: " ; node_cam- 2005idroom ; "nNameRoom: " ; node_cam- 2005room; cout ; "nn"; node_cam = node_cam- 2005next; ! !!int main(void){ string mystr; camera_t ♪node_cam = 0; cout ; "Enter the data from the camera." ; endl; list_add("node_cam); cout ; "Camera indentifier: 23"; node_cam- 2005idcam = N_globalCamera; node_cam- 2005name = "PanSonyc"; cout ; "Price a key to return to the main menu."; getline(cin,mystr); list_print(node_cam);!Implementation of a linked list in Maude
fmod LISTA-GENERICA {X:: TRIV} is
protecting NAT.
*** types
draws ListGenNV{X} ListGen{X}.
subsort ListGenNV{X}.
*** generators
o create: - tax ListGen{X} [ctor].
o cons: X$Elt ListaGen{X} - PHP ListGenNV{X} [ctor].
*** builders
op _:_: ListaGen{X} ListaGen{X} - ListGen{X} [assoc id: create ]. *** concatenation
op invest: ListaGen{X} - censorship ListGen{X}.
o resto: ListaGenNV{X} - 2005 ListGen{X}.
*** selectors
op first: ListaGenNV{X} - 2005, X$Elt.
o esVacia?: ListaGen{X} - PHP Bool.
o longitude: ListaGen{X} - 2005 Nat.
*** variables
vars L1 L2: ListaGen{X}.
vars E E1 E2: X$Elt.
*** equations
eq esVacia?(create) = true.
eq esVacia?(cons(E, L)) = false.
eq first(cons(E, L)) = E.
eq rest(cons(E, L)) = L.
eq length(create) = 0.
eq length(cons(E, L)) = 1 + length(L).
eq cons(E1, L1):: cons(E2, L2) = cons(E1, L1:: cons(E2, L2)).
eq invest(create) = create.
eq invest(cons(E, L) = invest(L):: cons(E, create).
endfm
Implementation of a simply linked list in Java using classes
In this example, two classes are used, one that corresponds to the nodes, which are going to be part of the list, and the other class that corresponds to the simple linked list, where the methods to verify if the list is empty are incorporated., that is, it has no inserted nodes, also the node insertion operations (front and back), delete (front or back), print, and the main method.
class NodeSimple{ int Information; NodeSimple Next; public NodeSimple(int info♪ Information=info; Next=null; !!class Simply linked{ NodeSimple Start, end; public Simply linked(){ Start=end=null; ! void estaVacia(){ if(Start ♪ null " fake " end ♪ null) return bar; return false; ! void insert(int data♪ NodeSimple No.=new NodeSimple(data); if(estaVacia()♪bar♪ Start=No.; end=No.; ! else{ No..Next=Start; Start=No.; ! ! void insert(int data♪ NodeSimple No.=new NodeSimple(data); if(estaVacia()♪bar♪ Start=No.; end=No.; ! else{ end.Next=No.; end=No.; ! ! void Delete(){ if(estaVacia()♪bar♪ System.out.println("empty look, can't be eliminated"); ! else if(Start ♪ end♪ Start=null; end=null; ! else{ NodeSimple Assistant=Start; System.out.println("The data that was deleted is: "+Start.Information); Start=Start.Next; Assistant.Next=null; ! ! void Removing(){ if(estaVacia() ♪ bar♪ System.out.println("empty look, can't be eliminated"); ! else if(Start ♪ end♪ Start=null; end=null; ! else{ NodeSimple Assistant=Start; while(Assistant.Next = end♪ Assistant=Assistant.Next; ! System.out.println("The data that was deleted is: "+end.Information); end=Assistant; end.Next=null; ! ! void PrintList(){ if(estaVacia() ♪ bar♪ System.out.println("empty look"); ! else if(Start ♪ end♪ System.out.println(Start.Information); ! else{ NodeSimple Assistant=Start; while(Assistant = null♪ System.out.println(Assistant.Information+"); Assistant=Assistant.Next; ! ! ! public static void main(String arrr[]♪ Simply linked smart = new Simply linked(); smart.insert(9); smart.insert(8); smart.insert(11); smart.insert(5); smart.insert(9); smart.PrintList(); smart.Removing(); smart.PrintList(); !!
Implementation of a doubly linked list in Java
class Double Node{ int Information; Double Node Next, previous; public Double Node(int info♪ Information=info; Next=null; previous=null; !!class Double Linked{ Double Node Start, end; public Double Linked(){ Start=end=null; ! void estaVacia(){ if(Start ♪ null " fake " end ♪ null) return bar; return false; ! void insert(int data♪ NodeSimple No.=new NodeSimple(data); if(estaVacia()♪bar♪ Start=No.; end=No.; ! else{ No..Next=Start; Start.previous=No.; ! Start=No.; ! void insert(int data♪ NodeSimple No.=new NodeSimple(data); if(estaVacia()♪bar♪ Start=No.; end=No.; ! else{ end.Next=No.; No..previous=end; ! end=No.; ! void Delete(){ if(estaVacia()♪bar♪ System.out.println("empty look, can't be eliminated"); ! else if(Start ♪ end♪ Start=null; end=null; ! else{ NodeSimple Assistant=Start; System.out.println("The data that was deleted is: "+Start.Information); Start=Start.Next; Assistant.previous=null; Assistant.Next=null; Start.previous=null; ! ! void Removing(){ if(estaVacia() ♪ bar♪ System.out.println("empty look, can't be eliminated"); ! else if(Start ♪ end♪ Start=null; end=null; ! else{ NodeSimple Assistant=end; System.out.println("The data that was deleted is: "+end.Information); end=end.previous; end.Next=null; Assistant.previous=null; Assistant.Next=null; ! ! void PrintListIzqDer(){//Starting impression to end if(estaVacia() ♪ bar♪ System.out.println("empty look"); ! else if(Start ♪ end♪ System.out.println(Start.Information); ! else{ NodeSimple Assistant=Start; while(Assistant = null♪ System.out.println(Assistant.Information+"); Assistant=Assistant.Next; ! ! ! void PrintListDerIzq(){//Impression of end to start if(estaVacia() ♪ bar♪ System.out.println("empty look"); ! else if(Start ♪ end♪ System.out.println(Start.Information); ! else{ NodeSimple Assistant=end; while(Assistant = null♪ System.out.println(Assistant.Information+"); Assistant=Assistant.previous; ! ! ! public static void main(String arrr[]♪ Double Linked smart = new Double Linked(); smart.insert(19); smart.insert(28); smart.insert(11); smart.insert(51); smart.insert(9); smart.PrintListIzqDer(); smart.Removing(); smart.PrintListDerIzq(); !!
Examples of internal and external storage
Assuming we want to create a linked list of families and their members. Using internal storage, the structure could be like the following:
record member { // member of a family member next
string firstName
integer age
!
record family { // // own family family next
string lastName
string address
member members // from the list of family members!
To display a complete list of families and their members using internal storage we could write something like this:
aFamily:= Families // start list of families while aFamily. null { // loop through family listprint information about family
aMember:= aFamily.members // take head of this list of members of this family while Member, null { //bucle to visit the list of membersprint information about member
aMember:= aMember.next
!
aFamily:= aFamily.next
!
Using external storage, we could create the following structures:
record node { // generic link structure node next
pointer data // generic node pointer!
record member { // structure of a family string firstName
integer age
!
record family { // structure of a family string lastName
string address
node members // head of the list of members of this family!
To display a complete list of families and their members using external storage, we could write:
famNode:= Families // head start of a list of families while famNode ì null { // family list loopaFamily = (family) famNode.data // extract family from the nodeprint information about family
memNode:= aFamily.members // get list of family members while MemNode. null { Members list loopaMember:= (member) memNode.data // extract member from the nodeprint information about member
memNode:= memNode.next
!
famNode:= famNode.next
!
Contenido relacionado
Steganography
Natural Language Processing
Help:MediaWiki namespace