Lens

A lens.

Lenses can be used to focus light.

A lens is a transmitting optical device that focuses or scatters a beam of light through refraction. However, other devices such as Fresnel lenses, which bend light Through the phenomenon of diffraction, they are of great utility and use due to their low construction cost and the small space they occupy. Devices that similarly focus or scatter waves and radiation other than visible light are also called lenses, such as microwave lenses, electron lenses, acoustic lenses, or blast lenses.

A lens consists of a transparent medium bounded by two surfaces, at least one of which is curved. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements)., generally arranged along a common axis. Lenses are made of materials such as glass or plastic, and are ground and polished (or shaped) to achieve the desired shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing.

The most common lenses are based on the different degree of refraction experienced by light rays when they hit different points on their surface, including those used to correct vision problems in glasses, glasses or contact lenses. Lenses, or lens-mirror combinations, are also used in telescopes and microscopes to serve as objectives or eyepieces. The first astronomical telescope was built by Galileo Galilei using a converging lens (positive lens) as an objective and a diverging lens (negative lens) as an eyepiece. There are also instruments capable of converging or diverging other types of electromagnetic waves and which are also called lenses. For example, in electron microscopes the lenses are magnetic in nature.

In astrophysics it is possible to observe gravitational lensing phenomena, when light coming from very distant objects passes close to massive objects, and bends in its trajectory.

Etymology

The word lens comes from the Latin lens, lentis which means "lentil", so optical lenses are called that way because of their resemblance to the shape of a legume.

In the 13th century, small glass disks began to be made that could be mounted on a frame. They were the first book glasses or reading glasses.

The word lens is often ambiguous in gender. It is normally used in the feminine to refer to optical glass, while in the masculine and plural it is usually reserved to refer to glasses in some countries.

Parts of a lens

The different elements that make up a lens are the following:

• Curve centers (C, C'): it is the radius that establishes the curved surface of the lens, the incident and the emergent.

• Main or optical axis: imaginary straight line that unites the curvature centers of the lenses.
• Side effects: rays that pass through the optical center without deviating.
• Optical center (O): place where the main axis and lens converge.
• Foco main or object focus (F,F'): it is the place of the central axis where the refracted rays are transferred in the lens from parallel rays to the central axis.
• Main plan: normal plane to the main axis crossing the point of contact between the lightning and the incident surface of the lens. There is a second main plane formed by the normal plane to the main axis and that transfers the point of contact of the lightning and the emerging surface of the lens.
• Focus distance (f, f'): distance between the main focus and the optical center. Its reverse is called lens power, expressed by diopters.

Types

The lenses, depending on the shape they take, can be convergent, divergent or camera:

• The glasses convergent (or positive) are thicker on the central and narrower sides. They are thus called because they unite (convergen), at a certain point that is called the image focus all beams parallel to the main axis that pass through them.

They can be:

Main types of lenses.

• Biconvexas: they have two convex surfaces.
• Planoconvexas: have a convex and a flat surface.
• Concavo-convexas (or convergent minscus): formed by a convex surface and another slightly concave.

• The glasses divergent (or negative) are thicker by the edges and present a very pronounced narrowness in the center. They are so called because they make to diverge (separate) all beams parallel to the main axis that pass through them, their extensions converge in the image focus that is on the left, contrary to the convergents, whose image focus is on the right. Therefore, divergent lenses cannot form a real image but, by projection of the rays to the plane where the object is located, they can form virtual images. They can be:

• Biconcavas: formed by two concave surfaces.
• Planoconcavas: have a concave surface and a flat surface.
• Convexo-concavas (or divergent menisco): they have a concave surface and the other is slightly convex.

Simple lens construction

Most lenses are spherical lenses: their two surfaces are parts of the surfaces of spheres. Each surface can be convex (bulging outward from the lens), concave (recessed into the lens), or planar (flat). The line joining the centers of the spheres that form the lens surfaces is called the lens axis. Normally the axis of the lens passes through the physical center of the lens, due to the way they are manufactured. Lenses can be cut or ground after they are made to give them a different shape or size. So the axis of the lens may not pass through the physical center of the lens.

Toric or spherocylindrical lenses have surfaces with two different radii of curvature in two orthogonal planes. They have a different focal power in different meridians. This forms an astigmatic lens. An example is spectacle lenses used to correct astigmatism in a person's eye.

Types of simple lenses

Lenses are classified by the curvature of the two optical surfaces. A lens is biconvex (or double convex or simply convex) if both surfaces are convex. If both surfaces have the same radius of curvature, the lens is equiconvex. A lens with two concave surfaces is biconcave (or simply concave). If one of the surfaces is flat, the lens is plano-convex or plano-concave depending on the curvature of the other surface. A lens with one convex and one concave side is convex-concave or meniscus. It is this type of lens that is most commonly used in corrective lenses.

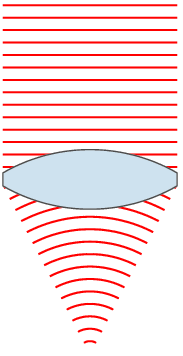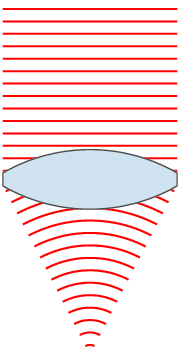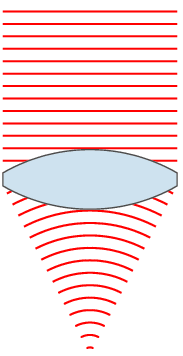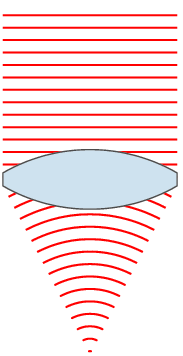
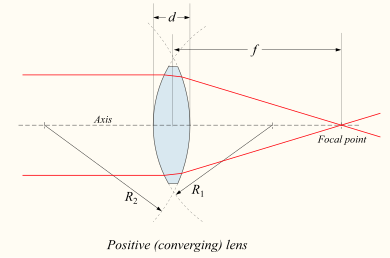
If the lens is biconvex or plano-convex, a collimated light beam passes through the lens and converges on a point (a focus) behind the lens. In this case, the lens is called a positive or converging lens. For a thin lens, the distance from the lens to the point is the focal length of the lens, which is commonly represented by f in diagrams and equations. An extended hemispherical lens is a special type of plano-convex lens, in which the curved surface of the lens is a complete hemisphere, and the lens is much thicker than the radius of curvature.

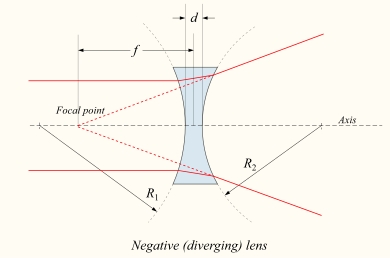
If the lens is biconcave or plano-concave, a collimated light ray passing through the lens is diverging (scattering); therefore, the lens is called a negative or diverging lens. The ray, after passing through the lens, appears to emanate from a particular point on the axis in front of the lens. For a thin lens in air, the distance from this point to the lens is the focal length, even though it is negative with respect to the focal length of a converging lens.

Convex-concave (meniscus) lenses can be positive or negative, depending on the relative curvatures of the two surfaces. A negative meniscus lens has a more pronounced concave surface and is thinner in the center than the periphery. In contrast, a positive meniscus lens has a more pronounced convex surface and is thicker in the center than at the periphery. An ideal thin lens with two surfaces of equal curvature would have zero optical power, meaning that light would neither converge nor diverge. However, all real lenses have a non-zero thickness, making a real lens with identical curved surfaces slightly positive. To obtain exactly zero optical power, a meniscus lens must have slightly unequal curvatures to account for the effect of lens thickness.

Lens Maker's Equation

The focal length of a lens in air can be calculated from the lens maker's equation:

1f=(n− − 1)[chuckles]1R1− − 1R2+(n− − 1)dnR1R2],{displaystyle {frac {1}{f}}}=(n-1)left[{frac {1}{R_{1}}}{frac {1}{1}{R_{2}}}}}}}}}{frac {(n-1)d}{nR_{1}R_{2}}{2}}},}

where

f is the focal distance of the lens

n{displaystyle n} is the refraction rate of the lens material

R1{displaystyle R_{1}} is the curvature radius (with sign, see below) of the lens surface closest to the light source

R2{displaystyle R_{2}} is the curvature radius of the lens surface farther from the light source

d{displaystyle d} is the thickness of the lens (the distance along the lens axis between the two surface vertices

The focal length f is positive for converging lenses and negative for diverging lenses. The multiplicative inverse of focal length, 1 / f is the optical power of the lens. If the focal length is in meters, this gives the optical power in diopters (reverse meters).

Lenses have the same focal length when light travels from back to front or when light travels from front to back. Other lens properties, such as aberrations, are not the same in both directions.

Sign convention for radii of curvature R 1 and R 2

Main article: Radius of curvature (optics)

The signs of the radii of curvature of the lens indicate whether the corresponding surfaces are convex or concave. The sign convention used to represent this varies, but in this article a positive R indicates that the center of curvature of a surface is further along in the direction of ray travel (right, in accompanying diagrams), while a negative R means that the rays reach the surface. They have already passed the center of curvature. Consequently, for external lens surfaces as shown in the diagram above, R ₁ > 0 and R ₂ <0 indicate convex surfaces (used to converge light onto a positive lens), while R ₁ <0 and R ₂ > 0 indicate concave surfaces. The reciprocal of the radius of curvature is called curvature. A flat surface has zero curvature and its radius of curvature is infinite.

Fine lens approximation

If d is small compared to R ₁ and R ₂ then the thin lens approximation can be made. For a lens in air, f is given by

1f≈ ≈ (n− − 1)[chuckles]1R1− − 1R2].{displaystyle {frac {1}{f}}}approx left(n-1right)left[{frac {1}{R_{1}}}}{frac {1}{R_{2}}}}}}{right]. !

Image formation

For the construction of an image, first a continuous ray is drawn and parallel to the main axis, which is refracted in the lens and crosses the optical axis. A second ray passes through the optical center of the lens without deflection until it intersects the previous ray. The last ray crosses through the main focus and passes through the lens, so that it is refracted inside the lens, which will intersect with the two previous rays in the optical axis.

In both types of lenses, converging and diverging, there are two ways to locate the mirror: either further from the lens than the main focus (real image) or between these two (virtual image). In the case of diverging lenses, there are these two options for positioning the mirror, but in both the images formed by this type of lens are virtual images, upright and smaller than the real objects.

In contrast, converging lenses in front of objects far away in space will project real images, inverted and smaller than the real objects. On the contrary, if a close object is observed through this lens, an upright image will be formed and larger than the real object, so that for a close distance they will form virtual images, upright and with larger dimensions.

The lenses or objectives used in photography are corrected to offer acceptable image quality and coverage over a given surface. In this way, a regulation of the visual angle is produced by means of the focal length in relation to the diagonal of the negative. When there is a change in focal length, there is also an alteration in the size of the image and therefore in the visual angle.

During this process in the adaptation behavior of the objectives, what are called geometric optical defects or aberrations can occur, which can affect the quality of the image. When referring to the precision and quality of an objective, we are talking about the ability to correct these defects, in such a way that it allows balancing the major aberrations in order to reduce them to a minimum, although it does not allow their complete elimination. The quality of an objective will be determined based on the degree of correction applied to seven main aberrations: two central ones, spherical and chromatic, and another five non-axial ones, coma, astigmatism, field curvature, curvilinear distortion, and side chromatic.

Artificial lenses

Instruments for the preparation of convex and concave lenses.

Artificial lenses are often called those built with inhomogeneous artificial materials, such that their behavior exhibits refractive indices less than unity (it should be remembered that the phase velocity can be greater than the speed of light in the empty), with which, for example, we have divergent biconvex lenses. Once again, this type of lens is useful in microwaves and only recently have materials with this property been described at optical frequencies.