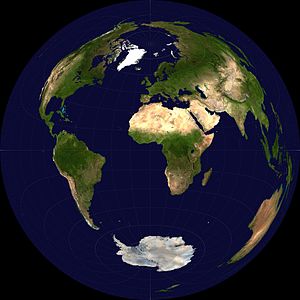
Lambert azimuthal projection
The Lambert Azimuthal Equal-Area (LAEA) projection deliberately preserves areas.
It is a particular projection from sphere to disk. It should not be confused with the Lambert Conformal Conical Projection which is widely used in air navigation. The Lambert azimuthal equivalent projection is not conformal, that is, it does not maintain the real value of the angles after performing the projection. The scale decreases as we get closer to the outer edge, but to a lesser extent than in the orthographic projection. This system is well suited for small-scale mapping.
History
The inventor of this projection is the German mathematician Johann Heinrich Lambert who in 1759 published a book with diverse reflections about the projection, the writing was titled "Freye Perspective" (There was a second improved edition in 1774). The writings on perspective and projection were expanded in 1943 by Max Steck bringing them together in a complete work.
Formulation
The distance from the point of tangency on the map is proportional to the distance in a straight line on the surface of the earth: r(d) = c sin(d/(2R)).
Advantages of projection
The great advantage of this projection system is that the areas represented on the maps do not undergo deformation and are proportional to the original shapes, complying with the following rule: «equal surfaces represent equal solid angles».